Задание 1. Найти предел функции, пользуясь правилом Лопиталя


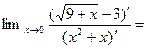
= 
Задание 2. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Будем следовать общему плану.
Построим координатную плоскость, на которую будем наносить результаты, полученные в
каждом разделе.
I. Общая характеристика функции.
1. Область определения  :
: 
Т. е 
2. Характеристика функции.
Функция  называется четной, если
называется четной, если  , нечетной, если
, нечетной, если  , иначе - функцией общего вида
, иначе - функцией общего вида


По определению,  - нечетная функция.
- нечетная функция.
3. Непрерывность функции.
 является непрерывной везде, кроме точек
является непрерывной везде, кроме точек  и
и  , где она терпит бесконечный
, где она терпит бесконечный
разрыв.
4. Точки пересечения графика функции с осями координат.


5. Асимптоты.
1. Вертикальные асимптоты связаны с точками бесконечного разрыва
 предел слева:
предел слева: 



предел справа: 


 предел слева:
предел слева: 


предел справа: 


2. Наклонные асимптоты.
 ;
;  ;
; 


Наклонная асимптота 
При  и при
и при  график функции
график функции  будет неограниченно приближаться к
будет неограниченно приближаться к
графику прямой  .
.
Полученные точки и асимптоты наносим на координатную плоскость.














Схематический график 1.
II. Исследование функции на возрастание и убывание, экстремумы.
1.Находим

2. 

или 

 ,
, 
 не существует, если
не существует, если  =0, т.е.
=0, т.е.  и
и  , но эти точки не входят в область
, но эти точки не входят в область
определения.
Нанесем полученные точки на ось 










Определяем знак первой производной в каждом полученном интервале, для чего определим
знак  в произвольной точке каждого интервала.
в произвольной точке каждого интервала.
Возьмем, например,  ,
,  ,
,  ,
,  ,
,  ,
, 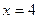 .
.




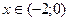







4. Определяем участки возрастания и убывания функции.



 функция убывает
функция убывает


 функция возрастает
функция возрастает

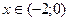
 функция возрастает
функция возрастает


 функция возрастает
функция возрастает


 функция возрастает
функция возрастает


 функция убывает
функция убывает
6. Определяем точки экстремума.
7. 

 Точка
Точка  -мининум
-мининум


 Точка
Точка  -максимум
-максимум


Нанесем точки экстремума на координатную плоскость.













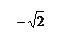




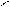

Схематический график 2.
III. Исследование функции на выпуклость, вогнутость и точки перегиба.
1. Находим вторую производную


2. 
 - не существует при
- не существует при  , т.е.
, т.е.  и
и  ; но эти точки не входят в область
; но эти точки не входят в область
определения  .
.
3. Нанесем эти точки на ось  .
.






Определяем знак второй производной в каждом полученном интервале, для чего определяем
знак 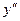 , например, в точках
, например, в точках  ,
,  ,
,  и
и 


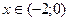





4. Определяем интервалы выпуклости и вогнутости функции

 - функция вогнутая
- функция вогнутая 
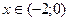
 - функция выпуклая
- функция выпуклая 

 - функция вогнутая
- функция вогнутая 

 - функция выпуклая
- функция выпуклая 
5. Определяем точки перегиба.
При переходе через 
 меняет знак (выпуклость меняется на вогнутость).
меняет знак (выпуклость меняется на вогнутость).
Определяем значение  в точке перегиба.
в точке перегиба.
 ; точка перегиба (0,0).
; точка перегиба (0,0).
Наносим точку перегиба на схематический график.




















Схематический график 3.






 IV. Строим график.
IV. Строим график.