Методические указания и задания
К контрольным работам студентов
I курса заочного отделения
(кроме ЗПМ)
Составители: Ваксман К.Г.
Михайлова А.В.
Москва,
2010 г.
Контрольная работа № 1
Контрольная работа содержит
задания по основным разделам
математики за курс средней школы
Основные теоретические сведения
Для успешного выполнения контрольной работы необходимо повторить по любому учебнику математики (Алгебра) следующие разделы:
1. Понятие модуля
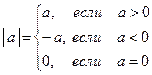 .
.
 – расстояние от точки х до а на числовой оси.
– расстояние от точки х до а на числовой оси.
2. Линейная функция 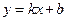 , свойства и график. Функция
, свойства и график. Функция 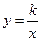 , свойства и график. Квадратный трехчлен
, свойства и график. Квадратный трехчлен 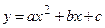 .
.
3. Определение 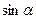 ,
, 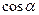 ,
, 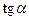 ,
, 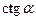 . Формулы:
. Формулы:  ,
, 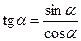 ,
, 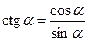 ,
, 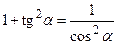 ,
, 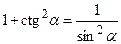 .
.
4. Тригонометрические функции 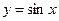 ,
, 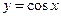 ,
, 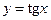 ,
, 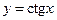 .
.
Основные свойства и графики (период функции, нули функции, наибольшее и наименьшее значения, участки возрастания, убывания).
5. Значение тригонометрических функций в точках 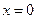 ,
, 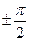 ,
, 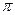 ,
, 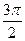 ,
, 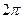 .
.
6. Основные тригонометрические формулы 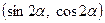 .
.
7. Степени, их свойства.
8. Показательная функция 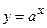 , свойства и график.
, свойства и график.
9. Логарифмическая функция 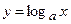 , свойства и график.
, свойства и график.
Пример решения контрольного задания
Задача 1. а) 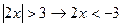 или
или 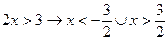 .
.




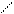
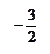
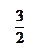
б) 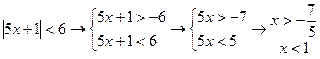
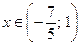
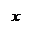
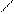
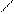
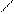
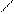
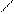
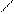
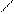
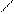
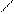
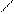




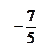
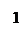
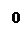












 в)
в) 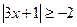 верно при всех х,
верно при всех х, 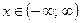
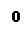



Задача 2. Построить графики функций 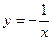 и
и 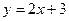 .Для построения составим таблицы
.Для построения составим таблицы
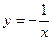 ,
, 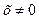

| –2 | –1 | –0,5 | 0,5 | |||

| 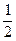
| – | –2 | –1 | 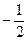
|
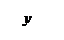
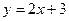

| –1 | |

|
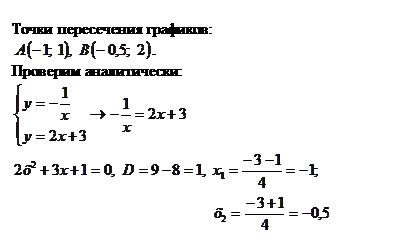


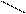

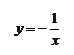
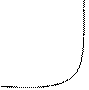

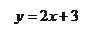


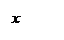
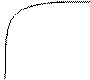
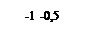
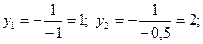 Точки пересечения
Точки пересечения 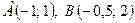 .
.
Задача 3. Дана функция 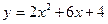 .
.
1) 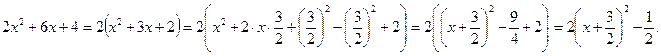
2) Нули функции 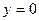 .
. 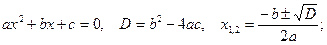
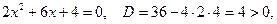
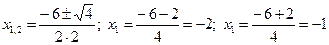 .
.
Для построения графика: абсцисса вершины 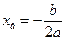 ,
, 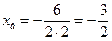 ;
;
ордината вершины 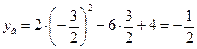 .
.
Для построения графика составим таблицу:

| –3 | –2 | – 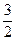
| –1 | |

| 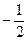
|
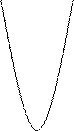


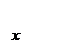

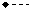
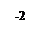
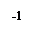


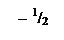
3) 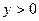 при
при 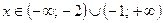
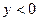 при
при 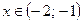 .
.
4)  возрастает при
возрастает при 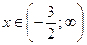
 убывает при
убывает при 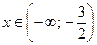 .
.
Задача 4. Даны функции 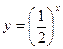 и
и 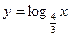 .
.
1) Построить графики. Для их построения составим таблицы.

| -1 | ||

| 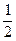
|


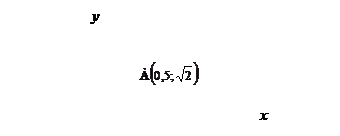
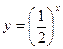
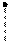

| 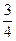
| 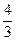
| 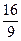
| |

| -1 |
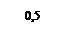

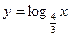
2) 

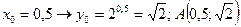 ;
;
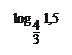
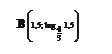


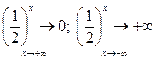 .
.
3) 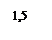

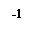



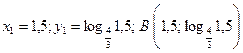 ;
;
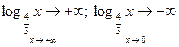
Задача 5.
1) 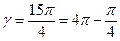 .
.
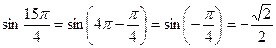 ;
;
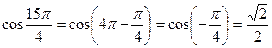 ;
;

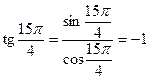 ;
; 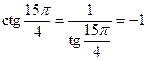 .
.
2) 


 Построить график
Построить график 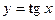 при
при 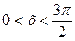 . Построим таблицу.
. Построим таблицу.

| 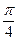
| 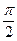
| 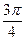
| 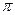
| 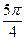
| 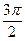
| |

| 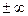
| -1 | 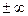
|
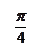
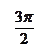
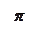
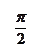
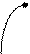
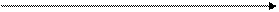
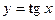 периодическая функция, период
периодическая функция, период 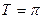 .
.
Нули функции: 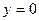 при
при 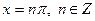 .
.
Наименьшее значение: 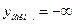 .
.
Наибольшее значение: 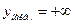 .
.
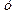 возрастает на данном интервале при
возрастает на данном интервале при 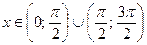 .
.
Задача 6. Вычислить
1) 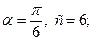
 .
.
2) 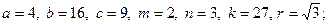
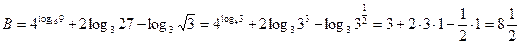 .
.
3) 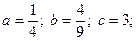
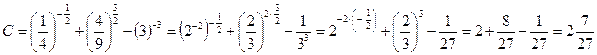 .
.
Задания к контрольной работе №1
(Значения буквенных параметров даны в вариантах контрольной работы)
Задача 1. Решить неравенства и показать решения на числовой оси 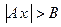 ,
, 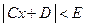 ,
, 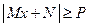 .
.
Задача 2. Построить графики функций на одном рисунке, указать их точки пересечения, проверить решение аналитически. 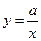 ,
, 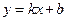 .
.
Задача 3. Дана функция 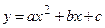 требуется:
требуется:
1) выделить полный квадрат из квадратного трехчлена и построить график функции; 2) найти нули функции по формуле корней квадратного уравнения; 3) определить, при каких значениях аргумента функция принимает положительные или отрицательные значения; 4) указать области возрастания и убывания функции.
Задача 4. Даны функции 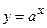 и
и 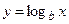 . Требуется: 1) построить графики функций; 2) показать на графике значение функции
. Требуется: 1) построить графики функций; 2) показать на графике значение функции 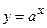 в точке
в точке 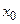 и указать поведение функции при
и указать поведение функции при 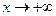 и
и 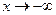 ; 3) показать на графике значение функции
; 3) показать на графике значение функции 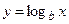 в точке
в точке 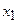 и указать поведение функции при
и указать поведение функции при 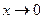 и
и 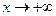 ;
;
Задача 5. Требуется: 1) построить на единичной окружности угол 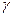 и вычислить
и вычислить 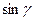 ,
, 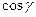 ,
, 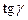 ,
, 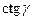 ; 2) построить график функции
; 2) построить график функции 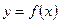 на заданном интервале
на заданном интервале 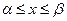 . Указать период функции, нули функции, её наибольшее и наименьшее значения, участки возрастания и убывания на заданном интервале х.
. Указать период функции, нули функции, её наибольшее и наименьшее значения, участки возрастания и убывания на заданном интервале х.
Задача 6. Вычислить следующие выражения:
1) 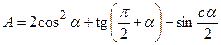 ;
;
2) 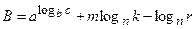
3) 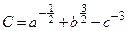 .
.
| № вар-та | Значения параметров | № вар-та | Значения параметров |
1) 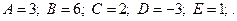
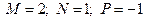 .
2) .
2) 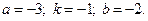 3)
3) 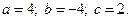 4)
4) 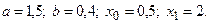 5)
5) 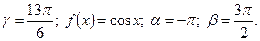 6) 1.
6) 1. 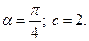 2.
2. 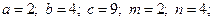
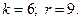 3.
3. 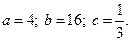
|
1) 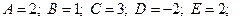
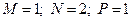 .
2) .
2) 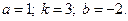 3)
3) 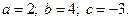 4)
4) 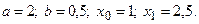 5)
5) 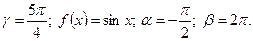 6) 1.
6) 1. 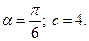 2.
2. 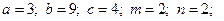
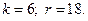 3.
3. 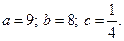
| ||
1) 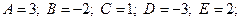
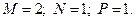 2)
2) 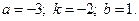 3)
3) 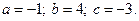 4)
4) 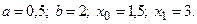 5)
5) 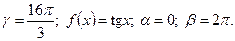 6) 1.
6) 1. 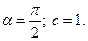 2.
2. 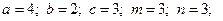
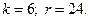 3.
3. 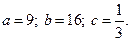
|
1) 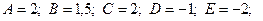
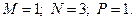 2)
2) 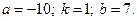 3)
3) 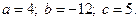 4)
4) 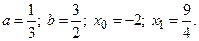 5)
5) 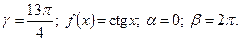 6) 1.
6) 1. 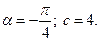 2.
2. 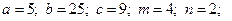
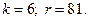 3.
3. 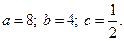
| ||
1) 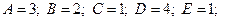
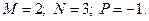 2)
2)  3)
3) 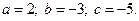 4)
4) 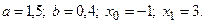 5)
5) 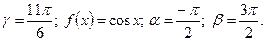 6) 1.
6) 1. 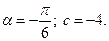 2.
2. 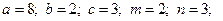
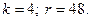 3.
3. 
| 1) 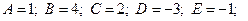
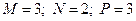 .
2) .
2) 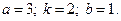 3)
3) 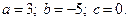 4)
4) 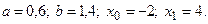 5)
5) 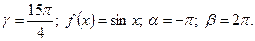 6) 1.
6) 1. 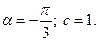 2.
2. 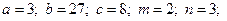
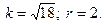 3.
3. 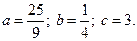
| ||
1) 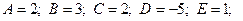
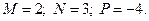 2)
2) 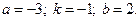 3)
3) 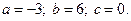 4)
4) 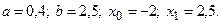 5)
5) 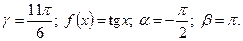 6) 1.
6) 1. 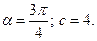 2.
2. 
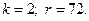 3.
3. 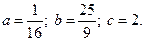
|
1) 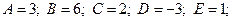
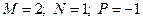 .
2) .
2) 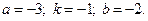 3)
3) 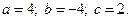 4)
4) 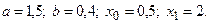 5)
5) 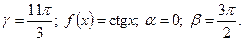 6) 1.
6) 1. 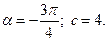 2.
2. 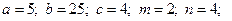
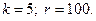 3.
3. 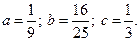
| ||
1) 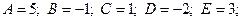
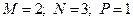 .
2) .
2) 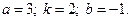 3)
3) 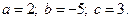 4)
4) 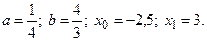 5)
5) 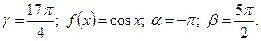 6) 1.
6) 1. 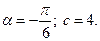 2.
2. 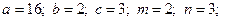
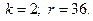 3.
3. 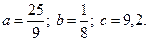
|
1) 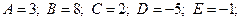
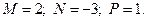 2)
2) 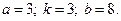 3)
3) 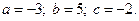 4)
4) 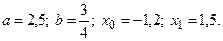 5)
5) 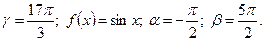 6) 1.
6) 1. 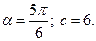 2.
2. 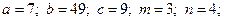
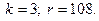 3.
3. 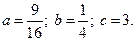
|
Контрольная работа № 2
Тема: «Пределы и непрерывность»
Основные теоретические сведения
(см. «Методические указания»)
- Символика
с – постоянная
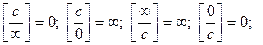
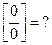 (неопределенность);
(неопределенность); 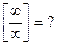 (неопределенность).
(неопределенность).
- Бесконечно-малые и бесконечно-большие функции
Функция  называется бесконечно-малой (бесконечно-большой) при
называется бесконечно-малой (бесконечно-большой) при 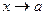 , если
, если 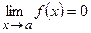 (
(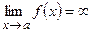 ).
).
- Предел отношения двух многочленов
1) 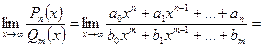
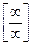 . Для раскрытия неопределенности
. Для раскрытия неопределенности 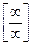 числитель и знаменатель требуется разделить на
числитель и знаменатель требуется разделить на 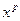 ,где
,где 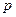 - наибольший показатель степени при
- наибольший показатель степени при  в числителе и знаменателе. Затем использовать, что
в числителе и знаменателе. Затем использовать, что 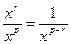 и
и 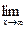
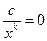 при
при 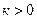 .
.
2) 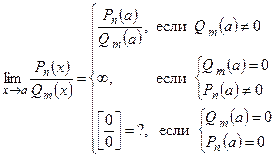
Для раскрытия неопределенности 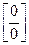 числитель и знаменатель требуется разложить на множители и сократить на общий множитель
числитель и знаменатель требуется разложить на множители и сократить на общий множитель 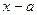 . Использовать формулы:
. Использовать формулы: 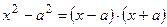 ;
;
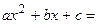
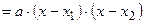 ,где
,где 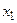 и
и 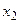 –корни,
–корни, 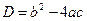 ,
, 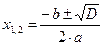 ;
;
- Первый замечательный предел
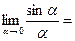
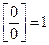 при
при 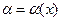 . Следствие:
. Следствие: 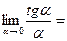
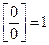 , так как
, так как 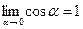 .
.
Сделав замену переменной 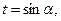 получим
получим 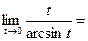
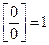 , аналогично:
, аналогично: 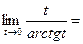
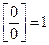 .
.
Использовать формулы: 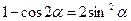 ;
; 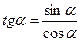 ;
; 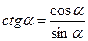 .
.
- Второй замечательный предел
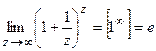 ;
; 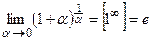 . Число
. Число 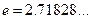
6. Функция 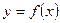 называется непрерывной в точке
называется непрерывной в точке 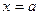 , если
, если 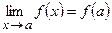 .
.
7. Условия непрерывности функции  в точке
в точке 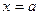 :
:
1) функция  должна быть определена в некотором интервале, содержащем точку а (т.е. в самой точке и вблизи этой точки);
должна быть определена в некотором интервале, содержащем точку а (т.е. в самой точке и вблизи этой точки);
2) функция должна иметь одинаковые односторонние пределы:
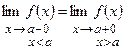 ;
;
3) эти односторонние пределы должны быть равны 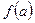 .
.






