Күні 14.10.1989 ж. ° Теодолит 2Т-30 Бакылаушы Сапаров Е.
Көрінуі жаксы № 10004 Жазушы Сорокина В.
| Тұру | Нысаналау | Вертикаль дөңгелектің орны | Горизонталь дөңгелектегі есептеулер | Бұрыш | Орта бұрыш |
| нүктелері | |||||
| А В А В | CD OD | 32°13'(1) 193в39'(2) 113в15'(4) 274-42'(5) | 161°26'(3) 161°27'(6) | 161°26,5'(7) |
Жүрістің оң жағындағы горизонталь бұрышты өлшеу және есептеу жоғарыдағы жүйелілікпен жүргізіледі, тек мұнда жүрістің оң жағындағы бұрыштың мәні әрбір жартылай тәсілде артқы және алдыңғы есептеулердің айырымы болып табылады
. (51)
Өлшенген бұрыштардың әрбір жартылай тәсілдегі мәнін және бұрыштың орташа мәнін теодолит станциядан алып қойылғанша есептеп шығарған жөн.
Қайталаулар әдісі. Горизонталь бұрышты қайталау жолымен өлшеу әдісі төмендегідей: 1) вертикаль дөңгелек сол жақта болғанда алидаданы 0°-қа жақын есептеуге қояды да, содан соң алидаданы бекітіп, лимбаны босатып артқы нүктені (А) нысаналап, a 
есептеуін алады; 2) лимба бекітулі күйде тұрғанда алидаданы босата отырып дүрбіні алдыңғы нүктеге (В) бағыттап, а2 есептеуін алады; 3) дүрбіні зенит аркылы ауыстырып, вертикаль дөңгелектің ок жақтағы орнына келтіреді; 4) лимбаны босатып, дүрбіні арткы нүктеге бағыттайды, бірақ есептеуді алмайды; 5) лимба бекітулі күйде тұрғанда, алидаданы босатып дүрбіні алдыкғы нүктеге бағыттайды да, а 
есептеуін алады.
Бір жартылай қайталау кезіндегі бұрыштық мәні бақылау мәні деп аталады, ол былайша анықталады:
(52)
Бір кайталаудан өлшенген бұрыштын орташа (соңғы) мәнін мына формула бойынша табады:
(53)
Бұрыштың соңғы және бакылау мәндерінің арасындары рұк-сат етілген айырмашылық теодолиттің есептеу құрылғысының бір жарым еселік дәлдігінен (t) аспауы керек, яғни
(54)
Айналма тәсілдер әдісі. Мұнда теодолитті нүктенің үстіне орналастырып, барлық бағыттарды сағат тілінің бағытымен жүйелі нысаналау жолымен есептеулер алады. Лимбаның орнынан қозғалмағандығына көз жеткізу үшін соңғы нысаналауды бастапқы бағытпен аяқтайды. Осы әрекеттер бірінші жартылай тәсілді кұрады. Екінші жартылай тәсілде лимбаны орнынан жылжытып, дүрбіні зенит арқылы ауыстырады да барлық бағыттарды сағат тілінің бағытына қарсы жүйелі нысаналайды..
Горизонталь бұрыштарды техникалық теодолиттермен өлшеудің дәлдігіне негізінен аспаптар мен нысаналаудың қателіктері, аспапты, қаданы орналастыру және есептеу қателіктері әсерін тигізеді.
Қазіргі кездегі теодолиттер тиісті жөндеулерден өткізілсе және өлшеудің лайықты методикасы қолданылса, онда қателіктер өте аз жіберілетін болады.
Аспапты және қаданы мұқият орналастырғанда және қабыр-ғаларының ұзындығының ең аз болуына шек қойылғанда центрлеу мен редукция қателіктерінің әсерін азайтуға мүмкіндік туады. Есептеудің қателігін есептеу құрылғысының дәлдігінің жартысына тең деп қабылдайды, яғни те =t/2.
Қорыта келгенде, металл лимбалы теодолиттермен бұрыштарды өлшегенде, оның дәлдігіне негізінен лимбадан алатын есептеулердің қателіктері әсерін тигізеді. Осыны еске алып, әрі қалған қателіктер бұрышты өлшеудің дәлдігіне елеулі әсерін тигізбейтінін біле отырып, мысал ретінде металл лимбалы теодолитпен бұрышты өлшеудің орташа квадраттық қателігін анықталық. Сонымен екінші есептеу құрылғысынан алатын санау есептеудің дәлдігін арттырмайды, ол тек қана алидаданың экс-центриситет қателігін жояды деп қабылдалық.
Бұрышты өлшегенде нүктені нысаналағаннан кейін лимбадан есептеулердің орташа квадраттық қателігін те =t/2 тең қателікпен жасайды. Осы кателікті өлшенілетін бұрыштың бағытының қателігі деп қабылдауға болады, өйткені жоғарыдағы айтылған шарттарға байланысты біз басқа қателіктер елеулі әсерін тигізбейді дегенбіз. Бұрыштың қателігі екі бағыттың айырымы болғандықтан, 
тең болады. Бір толық тәсілмен өлшенген бұрыштың орташа квадраттық қателігі
. (55)
Шекті (үш еселенген) қателік
(56)
Жартылай тәсілдердегі бұрыштың мәндерінің айырымының орташа квадраттық қателігі
(57)
Шекті қателік үшін орташа квадраттық қателіктің екі есе шамасын қабылдайды
(58)
Сондықтан бұрыштың екі мәнінің жартылай тәсілдердегі өзара айырмашылығы есептеу кұрылғысының екі есе дәлдігінен аспауы керек.
Вертикаль немесе көлбеу бұрыштарды вертикаль дөңгелектің көмегімен өлшейді. Вертикаль бұрыштарды өлшеу қолайлы болу үшін мынадай шарттар орындалуы тиіс: дүрбінің нысаналау осі мен алидадағы денгейдің осі горизонталь болған кезде алидаданың нөлдік бөліктері вертикаль дөңгелектік нөлдік бөліктерімен дәл келуі тиіс. Шындығында бұл шарт бұзылады, себебі дүрбінің нысаналау осі горизонталь орнында болса да, үлбіреуік нөл-пунктте тұрса да вертикаль дәңгелектегі есептеу нөлге тең болмауы мүмкін.
Дүрбінің нысаналау осі горизонталь, ал алидадағы деңгейдің үлбіреуігі нөл-пунктте болған уақыттағы вертикаль дөңгелектегі есептеуді вертикаль дөңгелектің нөлдік орны деп атайды, оны НО деп белгілейді.
Енді көлбеу бұрыштарды қалай өлшейтінін қарастыралық. Дүрбіні дөңгелектің он жақтағы (ОВ) кезіндегісімен кез келген М нүктесіне нысаналайды, деңгейдің үлбіреуігін ампуланың ортасына келтіргеннен кейін вертикаль дөңгелектен есептеу (ОD) алады. Осы есептеу 47-суретте көрсетілгендей көлбеу бұрыштан НО шамасына артық болады. Сондықтан
. (59)
Вертикаль дөңгелек сол жақта (СD) орналасқанда да жоғарыдағыға ұқсас әрекеттер орындалады. 47-суретте көрсетілгендей, СD есептеуі мұнда да келбеу бұрыштан НО шамасына артық болады, яғни
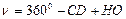(60)
немесе
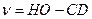(61)
(59) және (61) теңдіктерді НО және ν-ге қатысты шешіп, мынаны табамыз:
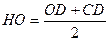(62)
|
| 47-сурет |
(63)
Вертикаль бұрыштарды есептеу қолайлы болу үшін вертикаль дөңгелектің нөлдік орны нөлге жуық болуы тиіс. Осы шартты орындау үшін бірнеше рет нөлдік орнының мәнін дүрбі торының горизонталь сызығын әр түрлі нүктелерге вертикаль дөңгелектің екі орнында нысаналау арқылы анықтайды. Егер нөлдік орнының есептелген мәні верньердің екі есе дәлдігінен артық болса, онда оны былайша азайту керек болады. Вертикаль дөңгелектің алидадасындағы жетекші винттің көмегімен деңгейдің үлбіреуігін ортасына келтіреді. Дүрбінің жетекші винтімен жұмыс істеп, вертикаль дөңгелектегі есептеуді нөлдік орнының есептелген орташа мәніне қояды. Осы жағдайда дүрбінің нысаналау осі горизонталь орнына келеді.
Енді деңгейдің осі мен дүрбінің нысаналау осі горизонталь орнында тұрғанда алидаданы верньердегі есептеу 0°-қа тең болғанша бұру кажет. Ол үшін алидаданың жетекші винтімен вертикаль дөңгелек пен верньердің нөлдерін беттестіреді (деңгейдің үлбіреуігі, әрине ортасынан жылжиды). Деңгейдің жөндеу винттерімен жұмыс істеп үлбіреуікті ампуланың ортасына келтіреді. Дұрыстығын білу үшін тексеруді кайталайды.
T30 теодолитінің нөлдік орнын жөндеген уақытта көлбеу бұрышты вертикаль дөңгелектің екі жағдайында анықтайды. Содан кейін дүрбіні бақылайтын нүктеден жылжытпай дөнгелек сол жақта болған кезде дүрбінің жетекші винтімен ν-ге тең есептеуді қояды. Осы кезде тордың горизонталь сызығы бақыланып отырған нүктеден жылжиды. Тордың вертикаль жөндеу винттерінің көмегімен сызықты бақылайтын нүктемен беттестіреді.
Вертикаль бұрыштарды өлшеудің дәлдігі негізінен есептеу кезінде жіберілетін қатесімен сипатталады. Вертикаль бұрыштарды өлшеудің орташа квадраттық қателігі есептеу кұрылғысының дәлдігінің жартысына тең деп қабылданады.
