1.Матрицаның анықтамасы.
2. Жол матрица дегеніміз не?
3. Баған матрица дегеніміз не?
4. Квадрат матрица дегеніміз не?
5. Диагональ матрица дегеніміз не?
6. Бірлік матрица дегеніміз не?
7. Үшбүрышты матрица дегеніміз не?
8. Матрицаларға қолданылатын амалдар.
9. Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері.
10. Матрицаларды көбейту амалының қасиеттері.
11. Екінші ретті анықтауыштың анықтамасы және есептелінілуі.
12. Үшінші ретті анықтауыштың анықтамасы және есептелінілуі.
13.  элементінің миноры дегеніміз не?
элементінің миноры дегеніміз не?
14.  элементінің алгебралық толықтауышы дегеніміз не?
элементінің алгебралық толықтауышы дегеніміз не?
15. Анықтауыштың қасиеттері.
16. Матрицаның рангі.
17. Матрицаны түрлендіру.
18. Кері матрица.
19. Жүйенің шешімі дегеніміз не?
20. Қандай жүйе үйлесімді деп аталады?
21. Қандай жүйе үйлесімсіз деп аталады?
22. Сызықты теңдеулер жүйесін шешу тәсілдері.
23. Вектордың анықтамасы.
24. Вектордың ұзындығының формуласы.
25. Вектордың орты.
26. Коллинеар векторлар.
27. Компланар векторлар.
28. Векторларға қолданылатын сызықтық амалдар.
29. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
30. Сызықтық тәуелді және тәуелсіз векторлар.
31. Векторды координат өстердің орттары арқылы жіктеу.
32. Вектордың модулі.
33. Вектордың бағыттаушы косинустары.
34. Координаттарымен берілген векторларға амалдар қолдану.
35. Кесіндіні берілген қатынаста бөлу формулалары.
36. Кесіндінің ортасын табу формуласы.
37. Векторлардың скалярлық көбейтіндісі.
38. Векторлардың в екторлық көбейтіндісі.
39. Векторлардың аралас көбейтіндісі.
40. Жазықтықтағы түзулердің әртүрлі теңдеулері.
41. Түзулердің арасындағы бұрыш.
42. Екі түзудің параллельдік және перпендикулярлық шарттары.
43. Нүктеден түзуге дейінгі қашықтық.
44. Жазықтықтың әртүрлі теңдеулері.
45. Екі жазықтықтың арасындағы бұрыш.
46. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
47. Нүктеден жазықтыққа дейінгі қашықтық.
48. Кеңістіктегі түзудің әртүрлі теңдеулері.
49. Түзу мен жазықтықтың өзара орналасуы.
50. Эллипстің канондық теңдеуі.
51. Гиперболаның канондық теңдеуі.
52. Параболаның канондық теңдеуі.
53. Екінші ретті беттердің канондық теңдеулері.
54. Функцияның анықтамасы.
55. Аралықта өсетін және кемитін функциялар.
56. Жұп және тақ функциялар.
57. Периодты функциялар.
58. Күрделі функция.
59. Кері функция.
60. Айқындалмаған функция.
61. Функцияның нүктедегі шегі.
62. Функцияның ақырсыздықтағы шегі.
63. Шексіз үлкен және шексіз аз шамалар.
64. Шектер туралы негізгі теоремалар.
65. Бірінші және екінші тамаша шектер.
66. Функцияның үзіліссіздігі. Үзілу нүктелерінің түрлері.
67. Функцияның туындысы.
68. Функцияның дифференциалы.
69. Жоғары ретті туындылар мен дифференциалдар.
70. Лопиталь ережесі.
71. Шексіз аздарды салыстыру.
72. Функцияның экстремумының қажетті шарты.
73. Функцияның экстремумының жеткілікті шарты.
74. Функцияның ойыстығы және дөңестігі
75. Функцияның графигінің асимптотасы.
76. Анықталмаған интеграл анықтамасы және қасиеттері.
77. Анықталмаған интегралды есептеу тәсілдері.
78. Анықталған интеграл және оның қасиеттері.
79. Анықталған интегралдың қолданылуы.
80. Меншіксіз интегралдар.
Глоссарий
| № | Жаңа түсініктер | Мағынасы |
| Матрица | m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кесте | |
| Квадрат матрица | матрицаның жолдарының саны бағандарының санына тең | |
| Диагональ матрица | квадрат матрицаның бас диагональдан тыс элементтері нөлге тең матрица | |
| Бірлік матрица | диагональ матрицаның бас диагоналі бір сандарынан тұратын матрица | |
| Транспонирленген матрица | жолдарын сәйкес бағандар етіп алмастырғаннан пайда болған матрица | |
| Бірінші ретті анықтауыш | кезкелген сан | |
| 2-ші ретті анықтауыш | 
| |
| А матрицасының рангі | осы матрицаның нөлге тең емес минорларының ең үлкен реті және оны  , ,  немесе немесе  деп белгілейді. деп белгілейді.  болады болады
| |
 элементінің алгебралық толықтауышы элементінің алгебралық толықтауышы
|  саны саны
| |
 матрицасына кері матрица матрицасына кері матрица
|  шарты орындалса, онда шарты орындалса, онда  матрицасын айтады оны матрицасын айтады оны 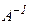 түрінде белгілейді. түрінде белгілейді.
| |
| Вектор | бағытталған кесінді | |
| Коллинеар векторлар | параллель түзулерде немесе бір түзудің бойында жататын векторлар | |
| Компланар векторлар | бір жазықтықта немесе параллель жазықтықтарда жататын кеңістіктегі үш вектор | |
| Вектордың модулі (ұзындығы) | 
| |
 және және  векторларының скалярлық көбейтіндісі векторларының скалярлық көбейтіндісі
|  саны саны
| |
 және және  векторларының скалярлық көбейтіндісі, егер векторларының скалярлық көбейтіндісі, егер

|

| |
| Түзудің бұрыштық коэффициент арқылы берілген теңдеуі |
 , ,  бұрыштық коэффициент бұрыштық коэффициент
| |
| Түзудің жалпы теңдеуі | 
| |
Екі түзудің арасындағы бұрыш
 және және 
| 
| |
| Нүктеден түзуге дейінгі қашықтық | 
| |
| Жазықтықтың жалпы теңдеуі |  , ,  нормаль вектор нормаль вектор
| |
| Түзудің канондық теңдеуі |  , ,  -бағыттаушы вектор -бағыттаушы вектор
| |
| Шеңбердің теңдеуі |  , ,  центрі, центрі,  радиусы радиусы
| |
| Эллипстің канондық теңдеуі |  , ,  эллипстің жарты өстері эллипстің жарты өстері
| |
| Гиперболаның канондық теңдеуі |  , ,  нақты, нақты,  жорамал жарты өстері жорамал жарты өстері
| |
| Параболаның канондық теңдеуі |  , ,  фокус пен директрисаға дейінгі ара қашықтық фокус пен директрисаға дейінгі ара қашықтық
| |
| Жұп функция | 
| |
| Функция | 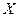 жиынының кез келген жиынының кез келген  элементіне белгілі бір заңдылықпен элементіне белгілі бір заңдылықпен 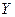 жиынының бір жиынының бір  элементі сәйкес келетін болса, онда элементі сәйкес келетін болса, онда 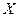 жиынында жиынында  функциясы берілді дейді. функциясы берілді дейді.
| |
| Тақ функция | 
| |
| Kүрделі функция | 
| |
| Айқындалмаған функция | 
| |
| Бірінші тамаша шек |  , ,
| |
| Екінші тамаша шект | 
| |
 функциясының функциясының 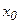 нүктесіндегі туындысы нүктесіндегі туындысы
|  ақырлы шегі ақырлы шегі
| |
| Функцияның дифференциалы | 
| |
 функциясының жергілікті минимум (максимум) нүктесі функциясының жергілікті минимум (максимум) нүктесі
| 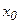 нүктесінің бір маңайында нүктесінің бір маңайында   теңсіздігі орындалса, онда осы нүктені айтады теңсіздігі орындалса, онда осы нүктені айтады
| |
| Жергілікті экстремум нүктелері | Жергілікті минимум және жергілікті максимум нүктелері | |
| Қисықтың асимптотасы | қисықтың  нүктесі шексіздікке ұмтылғанда нүктесі шексіздікке ұмтылғанда  нүктесінен түзуге дейінгі қашықтық нөлге ұмтылғандағы түзуді айтады нүктесінен түзуге дейінгі қашықтық нөлге ұмтылғандағы түзуді айтады
| |
| Қисықтың иілу нүктесі | ойыс және дөңес бөлігін бөліп тұратын нүктені деп атайды | |
 функциясының функциясының  аралығындағы алғашқы функциясы аралығындағы алғашқы функциясы
|  аралығында берілген аралығында берілген  функциясы үшін функциясы үшін  теңдігі орындалса, онда теңдігі орындалса, онда  функциясын айтады функциясын айтады
| |
 функциясының анықталмаған интегралы функциясының анықталмаған интегралы
| Егер  болса, онда болса, онда  функциясын айтады және ол функциясын айтады және ол  символымен белгіленеді, яғни символымен белгіленеді, яғни 
| |
| Ньютон- Л ейбниц формуласы |  
|






