ИДЗ-9.1(1,2,3,4,5,6,7,8)
Әдістемелік ұсыныс: Ньютон-Лейбниц формуласы анықталған интегралды есептеу үшін өте қолайлы құрал. Оны қолдану үшін интеграл астындағы жатқан функцияның бір алғашқы функциясын білу жеткілікті. Анықталған интегралды айнымалыны алмастыру және бөліктеп интегралдау әдістеріне есептер беріледі.
Ұсынылатын әдебиеттер: 9 нег. [181-205].
Тапсырма 15. Анықталған интегралдың қолданылуы. ИДЗ-9.2 (1,2,3,4)
Әдістемелік ұсыныс: Жазық фигураның ауданын және қисық доғаның ұзындығын әртүрлі координаттар жүйесіне есептеуге, айналу денесінің көлемін және бетін табуға да есептер беріледі.
Ұсынылатын әдебиеттер: 9 нег. [210-214].
Курс бойынша жазбаша жұмыстың тақырыптары
Бақылау жұмыстарының тақырыптары
1. Сызықтық алгебра
2. Векторлық алгебра
3. Аналитикалық геометрия
4. Анализге кіріспе
5. Бір айнымалы функциялардың дифференциалдық есептеулері
6. Анықталмаған интеграл.
7. Анықталған интеграл және оның қолданылуы
Ұсынылатын әдебиеттер: 1нег. [5-4371, 5 қос. [6-259], 20 қос. [10-253].
Здік бақылау үшін тест тапсырмалары
1. Егер анықтауштың қандай да бір жол элементтеріне сәйкес басқа жол элементтерін  санына көбейтіп қоссақ, онда анықтауыш
санына көбейтіп қоссақ, онда анықтауыш
A) таңбасы өзгереді; B)өзгермейді; C)таңбасы өзгермейді; D)  -есе артады; E)
-есе артады; E)  -есе азаяды.
-есе азаяды.
2.  және
және  түзулерінің арасындағы бұрышының тангенсін табыңыз:
түзулерінің арасындағы бұрышының тангенсін табыңыз:
A)  ; B)
; B)  ; C)
; C) 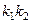 ; D)
; D)  ; E)
; E) 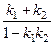 .
.
3. Егер түзу  векторының бағытымен
векторының бағытымен  нүктесінен өтсе онда, оның параметрлік теңдеуі мына түрде болады
нүктесінен өтсе онда, оның параметрлік теңдеуі мына түрде болады
A)  ; B)
; B)  ;
;
C)  ; D)
; D) 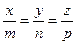 ; E)
; E) 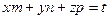 .
.
4. Егер жазықтық  нүктесінен өтіп
нүктесінен өтіп  векторына перпендикуляр болса, онда оның теңдеуі мына түрде болады
векторына перпендикуляр болса, онда оның теңдеуі мына түрде болады
A)  ; B)
; B)  ;
;
C)  ; D)
; D) 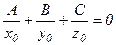 ; E)
; E)  .
.
5. Егер  ;
;  болса, онда
болса, онда  -ны тап
-ны тап
A)  ; B)
; B) 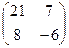 ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
6. Мына  анықтауыштың
анықтауыштың  алгебралық толықтауышын табыңыз
алгебралық толықтауышын табыңыз
A) –8; B) 22; C) -14; D) 14; E) -22.
7. Егер  болса, онда
болса, онда  -ны табыңыз
-ны табыңыз
A)  ; B)
; B) 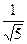 ; C)
; C)  ; D)
; D) 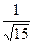 ; E)
; E)  .
.
8. Егер  болса, онда
болса, онда  -ны табыңыз
-ны табыңыз
A)  ; B)
; B) 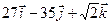 ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
9.  нүктесінен
нүктесінен 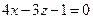 жазықтығына дейінгі қашықтықты табыңыз.
жазықтығына дейінгі қашықтықты табыңыз.
A) 1; B) -2; C) 2; D) 0; E) -1.
10.  және
және  түзулердің қиылысу нүктесін табыңыз.
түзулердің қиылысу нүктесін табыңыз.
A)  ; B)
; B)  ; C)
; C) 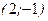 ; D)
; D)  ; E)
; E) 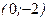 .
.
11. Шекті табыңыз: 
A) 0; B) 1; C) -1; D) 2; E) 3.
12. Шекті табыңыз: 
A) 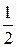 B) 1; C) 0; D) 5; E)
B) 1; C) 0; D) 5; E) 
13. Шекті табыңыз: 
A) –2; B) 0; C) 5; D)  ; E)
; E) 
14. Шекті табыңыз: 
A)  ; B) 1; C) 0; D) 2; E) шегі жоқ.
; B) 1; C) 0; D) 2; E) шегі жоқ.
15. Шекті табыңыз 
A) 0; B)  ; C) 3; D) 1; E) 5.
; C) 3; D) 1; E) 5.
16.  функциясының дифференциялының формуласын табыңыз.
функциясының дифференциялының формуласын табыңыз.
A)  ; B)
; B) 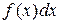 ; C)
; C) 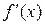 ; D)
; D)  ; E)
; E)  .
.
17.  функциясы
функциясы  ,
, 
 параметрлік түрде берілген. Осы функцияның
параметрлік түрде берілген. Осы функцияның 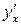 туындысын табыңыз.
туындысын табыңыз.
A)  ; B)
; B) 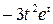 ; C)
; C) 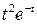 ; D)
; D)  ; E)
; E)  .
.
18.  функциясының
функциясының 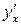 туындысын табыңыз.
туындысын табыңыз.
A) 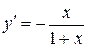 ; B)
; B) 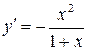 ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
19.  шегін Лопиталь ережесін қолданып табыңыз.
шегін Лопиталь ережесін қолданып табыңыз.
A) -1; B)  ; C) 1; D)
; C) 1; D)  ; E) 0.
; E) 0.
20. 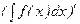 интегралы неге тең?
интегралы неге тең?
A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
21.  интегралы неге тең?
интегралы неге тең?
A)  ; B) 0; C)
; B) 0; C)  ; D)
; D) 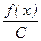 ; E)
; E)  .
.
22.  интегралы неге тең?
интегралы неге тең?
A)  ; B) 0; C)
; B) 0; C) 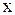 ; D)
; D)  ; E)
; E)  .
.
23.  интегралы неге тең?
интегралы неге тең? 
A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ;
;
E)  .
.
24.  интегралын есепте
интегралын есепте
A)  ; B)
; B)  ; C)
; C) 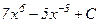 ; D)
; D)  ; E)
; E) 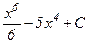 .
.
25.  интегралын есепте
интегралын есепте
A)  ; B)
; B)  ; C)
; C) 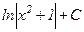 ; D)
; D)  ;Е)
;Е)  .
.
26.  интегралын есепте
интегралын есепте
A)  ; B)
; B) 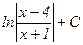 ; C)
; C)  ; D)
; D)  ;
;
E) 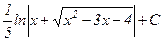
27.  интегралын есепте
интегралын есепте
A) 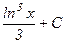 ; B)
; B) 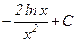 ; C)
; C)  ; D)
; D)  ; E) дұрыс жауабы жоқ
; E) дұрыс жауабы жоқ
28.  интегралын тап
интегралын тап
A)  ; B)
; B)  ; C)
; C) 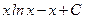 ; D)
; D)  ; E) дұрыс жауабы жоқ.
; E) дұрыс жауабы жоқ.
29.  интегралын есепте
интегралын есепте
A)  ; B)
; B)  ; С)
; С)  ; D)
; D)  ; E)
; E)  .
.
30. Мына 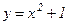 ,
, 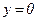 ,
,  ,
,  сызықтарымен қоршалған фигураның ауданын табыңыз.
сызықтарымен қоршалған фигураның ауданын табыңыз.
A) 6; B) 4; С)  ; D)
; D)  E) дұрыс жауабы жоқ.
E) дұрыс жауабы жоқ.
Дұрыс жауаптардың коды
| Сұрақтардың № | Дұрыс жауаптардың коды | Сұрақтардың № | Дұрыс жауаптардың коды | Сұрақтардың № | Дұрыс жауаптардың коды |
| B | A | C | |||
| D | E | E | |||
| C | A | A | |||
| A | C | A | |||
| A | B | B | |||
| E | E | D | |||
| D | B | A | |||
| A | A | C | |||
| C | A | E | |||
| D | D | A |






