Квадрат үшмүшелігі бар функцияларды интегралдау. Мына төмендегі интегралдарды табу әдісін қарастырайық  және
және  .
.
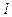 )
) 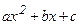 квадрат үшмүшелігіндегі
квадрат үшмүшелігіндегі 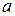 коэффициентін жақша алдына шығарып, одан толық квадратты бөліп аламыз;
коэффициентін жақша алдына шығарып, одан толық квадратты бөліп аламыз;
 ) интегралға
) интегралға  ,
, 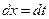 алмастыруын енгіземіз;
алмастыруын енгіземіз;
 ) Оны екі интегралдың қосындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралға келеді.
) Оны екі интегралдың қосындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралға келеді.
1- мысал. 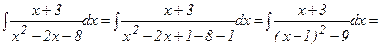
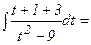
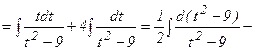

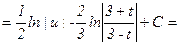
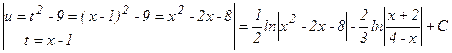 .
.
Рационал функцияларды интегралдау. Рационал бөлшекті интегралдау деп, 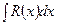 интегралын табуды айтады. Мұндағы
интегралын табуды айтады. Мұндағы 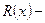 дұрыс рационал бөлшек, яғни
дұрыс рационал бөлшек, яғни 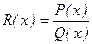
 . Егер
. Егер 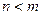 болса,
болса, 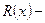 дұрыс бөлшек деп, ал
дұрыс бөлшек деп, ал 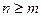 болса бұрыс бөлшек деп аталады. Бұрыс бөлшекті интегралдау үшін алдымен алымын бөліміне бөлу арқылы оны көпмүшелік пен дұрыс бөлшектің қосындысына жіктейміз. Мысалы,
болса бұрыс бөлшек деп аталады. Бұрыс бөлшекті интегралдау үшін алдымен алымын бөліміне бөлу арқылы оны көпмүшелік пен дұрыс бөлшектің қосындысына жіктейміз. Мысалы, 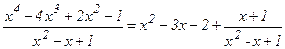 Одан әрі қарай тек дұрыс рационал бөлшектерді интегралдауды қарастырамыз.
Одан әрі қарай тек дұрыс рационал бөлшектерді интегралдауды қарастырамыз.
Теорема. Әрбір дұрыс рационал бөлшектімына қарапайым бөлшектердің қосындысы түрінде жазуға болады:
1. 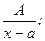 2.
2. 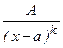
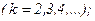 3.
3. 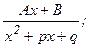 4.
4. 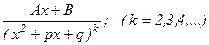 , мұндағы А, В - нақтыкоэффициенттер;
, мұндағы А, В - нақтыкоэффициенттер; 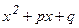 үшмүшелігінің нақты түбірлері жоқ (яғни
үшмүшелігінің нақты түбірлері жоқ (яғни  ). Қарапайым бөлшектерді интегралдауды қарастырайық.
). Қарапайым бөлшектерді интегралдауды қарастырайық.
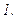
 .
.

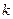
 мәнінде
мәнінде 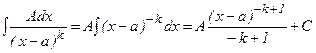 .
.
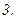
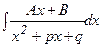 интегралдау әдісі жоғарыда қарастырылған.
интегралдау әдісі жоғарыда қарастырылған.
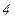 .
. 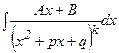 , мұндағы
, мұндағы  және бөліміндегі квадрат үшмүшеліктің дискриминанты
және бөліміндегі квадрат үшмүшеліктің дискриминанты 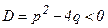 . Квадрат үшмүшеліктен толық квадрат бөліп алып
. Квадрат үшмүшеліктен толық квадрат бөліп алып 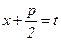 ,
, 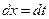 , алмастыруын жасаймыз. Сонда
, алмастыруын жасаймыз. Сонда 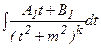 интегралын аламыз және оны екі интегралдардың қосындысы түрінде жазамыз. Бірінші интерал
интегралын аламыз және оны екі интегралдардың қосындысы түрінде жазамыз. Бірінші интерал 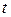 -ны дифференциал астына енгізу арқылы интегралданады:
-ны дифференциал астына енгізу арқылы интегралданады:

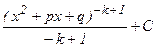 .
.
Ал екінші интегралды 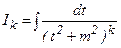 деп белгілеп, төменгідей есептейміз:
деп белгілеп, төменгідей есептейміз:

Бұл формуланы реккуренттік формула деп атайды. Реккуренттік формула арқылы 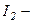 ні
ні 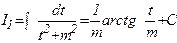 арқылы, ал
арқылы, ал 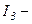 ті
ті 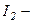 арқылы таба отырып, ең соңында
арқылы таба отырып, ең соңында 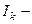 ны
ны 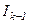 арқылы табамыз.
арқылы табамыз.
2- мысал. 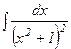 табу керек.
табу керек.  осыдан
осыдан 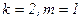 .
. 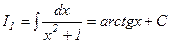 ,
, 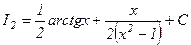 . Сонымен
. Сонымен 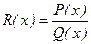 бөлшегінде
бөлшегінде 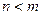 болсын. Әрбір
болсын. Әрбір 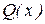 көпмүшелігін бірінші және екінші дәрежелі көпмүшеліктердің көбейтіндісіне жіктеп жазуға болады:
көпмүшелігін бірінші және екінші дәрежелі көпмүшеліктердің көбейтіндісіне жіктеп жазуға болады: 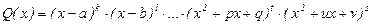 ,
,
мұндағы 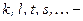 бүтін сандар. Сонда дұрыс бөлшек элементар бөлшектерге төменгідей жіктелінеді:
бүтін сандар. Сонда дұрыс бөлшек элементар бөлшектерге төменгідей жіктелінеді:
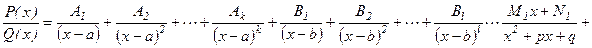
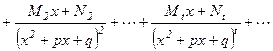
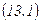
мұндағы 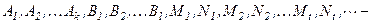 нақты сандар. Осы сандарды табу үшін
нақты сандар. Осы сандарды табу үшін 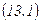 теңдігінің оң жағын ортақ бөлімге келтіреміз. Содан соң теңдіктегі екі бөлшектің бөлімін алып тастасақ, екі жағында да көпмүшелік шығады. Осы теңдіктен бірдей дәрежелі
теңдігінің оң жағын ортақ бөлімге келтіреміз. Содан соң теңдіктегі екі бөлшектің бөлімін алып тастасақ, екі жағында да көпмүшелік шығады. Осы теңдіктен бірдей дәрежелі 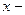 тің алдындағы коэффиценттерді теңестіре отырып, алгебралық теңдеулер жүйесін құрамыз. Алынған теңдеулер жүйесінен
тің алдындағы коэффиценттерді теңестіре отырып, алгебралық теңдеулер жүйесін құрамыз. Алынған теңдеулер жүйесінен  коэффиценттерінің мәндерін тауып, оларды
коэффиценттерінің мәндерін тауып, оларды 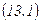 теңдігіне қоямыз. Осылай рационал бөлшектің жіктеуін табамыз. Осы әдісті анықталмаған коэффициенттер әдісі дейді.
теңдігіне қоямыз. Осылай рационал бөлшектің жіктеуін табамыз. Осы әдісті анықталмаған коэффициенттер әдісі дейді.
3-мысал.  интегралын есептеу керек. Интеграл астындағы функция бұрыс рационал бөлшек, сондықтан алымын бөліміне бөліп дұрыс бөлшекке айналдырамыз:
интегралын есептеу керек. Интеграл астындағы функция бұрыс рационал бөлшек, сондықтан алымын бөліміне бөліп дұрыс бөлшекке айналдырамыз:  Соңғы қосылғышты қарапайым бөлшектерге жіктейміз:
Соңғы қосылғышты қарапайым бөлшектерге жіктейміз: 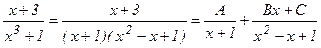
Бұдан, 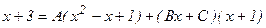
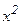 :
: 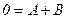 ;
;  :
: 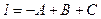 ;
; 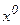 :
: 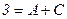
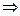
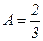 ,
, 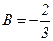 ,
,  . Демек,
. Демек, 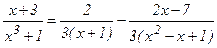 . Сонымен,
. Сонымен, 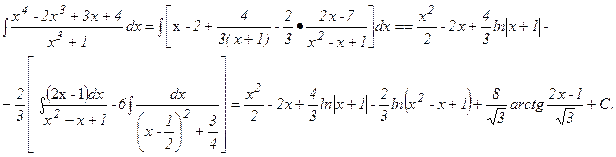
Кейбір иррационал функцияларды интегралдау. Иррационал функцияларды интегралдауда айнымалыны алмастыру арқылы рационал функцияның интегралына келуге болатын кейбір жағдайларды қарастырамыз. 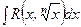 түріндегі интегралдар
түріндегі интегралдар 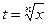 алмастыруы арқылы рационал функцияның интегралына келеді.
алмастыруы арқылы рационал функцияның интегралына келеді.
4- мысал. 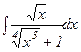 интегралын табайық.
интегралын табайық. 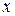 -тің дәрежесіндегі бөлшектердің ортақ бөлімі
-тің дәрежесіндегі бөлшектердің ортақ бөлімі 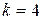 , олай болса берілген интегралды алу үшін
, олай болса берілген интегралды алу үшін 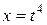 ауыстыруын жасаймыз.
ауыстыруын жасаймыз.
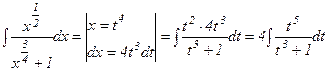
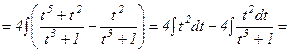

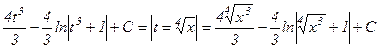 .
.
Қарастырылған интеграл 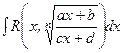 түріндегі интегралдың дербес түрі
түріндегі интегралдың дербес түрі
болады. Мұнда 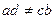 . Осы интегралды
. Осы интегралды 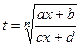 алмастыруы арқылы рационал функцияның интегралына келтіруге болады.
алмастыруы арқылы рационал функцияның интегралына келтіруге болады.
Тригонометриялық функцияларды интегралдау. Бұл пунктте біз 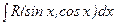 интегралын табуды қарастырамыз. Берілген интеграл
интегралын табуды қарастырамыз. Берілген интеграл 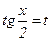 әмбебап алмастыруы арқылы рационал функцияның интегралына келтіріледі. Шынында да
әмбебап алмастыруы арқылы рационал функцияның интегралына келтіріледі. Шынында да
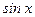
 ,
,  ,
,  ,
, 
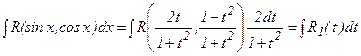 , мұндағы
, мұндағы 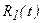 - рационал функция.
- рационал функция.
5- мысал.  .
.
Бұл әдісті көрсетілген кез келген интегралға қолдануға болады, ал 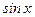 немесе
немесе 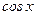 айнымалыларының дәрежесі бірден жоғары болса қолайсыз үлкен өрнектер шығады. Ондай жағдайларда келесі әдістерді қолдану керек.
айнымалыларының дәрежесі бірден жоғары болса қолайсыз үлкен өрнектер шығады. Ондай жағдайларда келесі әдістерді қолдану керек.
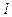 .
. 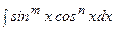 түріндегі интеграл.
түріндегі интеграл.
а) 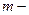 бүтін оң тақ сан болса, интеграл
бүтін оң тақ сан болса, интеграл 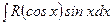 түріне келтіріліп,
түріне келтіріліп, 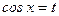 алмастырылуы жасалынады.
алмастырылуы жасалынады.
б) 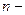 бүтін оң тақ сан болса, интеграл
бүтін оң тақ сан болса, интеграл  түріне келтіріліп,
түріне келтіріліп, 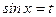 алмастырылуы жасалынады.
алмастырылуы жасалынады.
6- мысал. 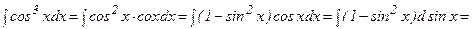
 .
.
в) 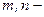 бүтін теріс емес жұп сан болса,
бүтін теріс емес жұп сан болса, 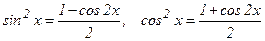 формулалары арқылы
формулалары арқылы 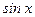 пен
пен 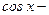 тің реттері төмендетіледі.
тің реттері төмендетіледі.
 . Мына
. Мына  , мұндағы m, n – тұрақты сандар, түріндегі интегралды алу үшін тригонометрияның формулаларын:
, мұндағы m, n – тұрақты сандар, түріндегі интегралды алу үшін тригонометрияның формулаларын:

қолдану және көбейтінділерді қосындыға жіктеу арқылы берілген интегралды алу қиынға түспейді.
Әдебиеттер: 1 нег.[372-382], 11 қос. [467-478].
Бақылау сұрақтар:
1. Құрамында квадрат үшмүшелігі бар функцияны интегралдау.
2. Рационал функциялар қалай интегралданады?
3. Әмбабап алмастыру деп қандай алмастыруды айтамыз?
4. Иррационал функцияларды интегралдау.






