Тапсырмалар: АЖ: 7 нег. 1154, 1165, 1185, 1187, 1678, 1679, 1706, 1709, 1712, 1714, 1717, 1720, 1725,1728, 1734, 1832, 1846, 1873, 1881.
Әдістемелік ұсыныстар: Функцияны зерттеудің жалпы сұлбасы (схемасы) және оның графигін салу дәрісін қайталап, тапсырмадағы есептерді шығарасыздар. Ол үшін функцияның өсу және кему аралықтарын, экстремумын, ойыс және дөңес аралықтарын, иілу нүктесін, асимптоталарын табуды үйден қарап келулеріңіз керек. Берілген кесіндіде функцияның ең үлкен және ең кіші мәндерін табуға да есептер шығарасыздар. Сонымен қатар анықталмаған интеграл тақырыбына есептер шығарасыздар. Бұнда интегралдар кестесін жаттап алу керек. Себебі функцияны интегралдағанда осы кестеге келтіріліп отырылады. Осы сабақта интералдаудың негізгі әдістеріне есептер шығарасыздар.
1. 
функциясының 
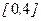кесіндісіндегі ең үлкен және ең кіші мәндерін есептеу керек.
Шешімі.Функцияның ең үлкен және ең кіші мәндері не критикалық нүктелерде, не кесіндінің шеткі нүктелерінде жатады. Сондақтан: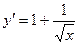 
, осыдан 
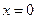- критикалық нүкте. Функцияның кесіндінің шеткі нүктелеріндегі мәні: 
.
Осыдан, функцияның ең кіші мәні 0, ал ең үлкен мәні 8 тең.
2. 
функциясын зерттеп, графигін салу керек.
Шешім:. 1)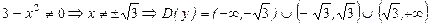 
2) 
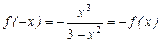, яғни тақ функция. Сондықтан функцияның графигі бас нүктеге қарағанда симметриялы. Демек зерттеуді 
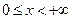аралығында жүргіземіз. Содан соң функцияның симметриялығын пайдаланамыз.
3) 
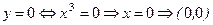- координата өстерімен қиылысу нүктелері.
4). 
. 
.
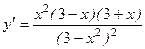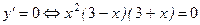
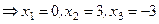Зерттеуді 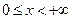аралығында жүргізетіндіктен 
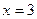нүктесін зерттейміз.. Осы нүктенің маңайында туындының таңбасын анықтаймыз.
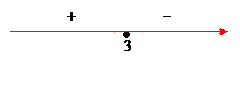
Демек,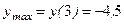 
; 
аралығында функция өседі және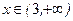 
аралығында функция кемиді.
5). 
.
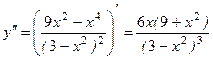Осыдан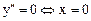 
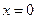. және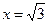 
нүктелерінің маңайында 
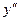таңбасын анықтаймыз.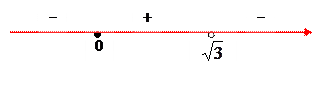 
Демек,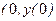 
), яғни 
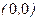– иілу нүктесі; қисық 
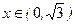аралығында ойыс және 
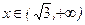аралығында дөңес болады.
6) 
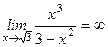, демек, 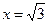- вертикаль асимптота.
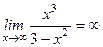, яғни горизонталь асимптотасы жоқ.
, 
.
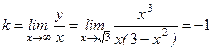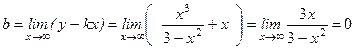Сонымен,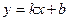 
, т.е. 
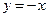көлбеу асимптота.
7). 
; 
; 
.
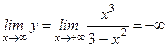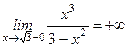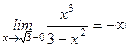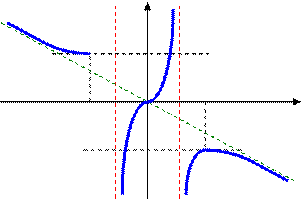Функцияның графигін сызамыз.
3. 
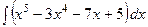интегралын есептеу керек.
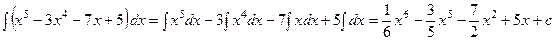
4. 
интегралын есептеу керек.
Шешімі.Интеграл астындағы функцияның алымындағы 1-ді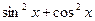 
өрнегімен ауыстырып және интегралдар кестесіндегі формулаларды қолдансақ
= 
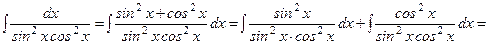
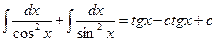
5. 
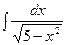интегралын есептеу керек.
Шешімі.Таблицалық интегралды пайдаланып, 
десек, онда 
.
6. 
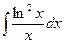интегралын есептеу керек.
Шешімі.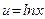 
деп алып және 
дифференциал таңбасының астына енгіземіз, онда
.
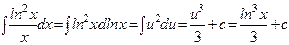7. 
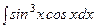интегралын есептеу керек.
Шешімі. 
функциясын дифференциал таңбасы астына енгізсек, яғни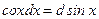 
, онда 
8. 
интегралын есептеу керек.
Шешімі.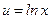 
, 
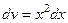деп алсақ және 
; 
.
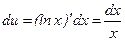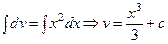Мұнда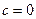 
деп аламыз, себебі алғашқы функцияның біреуін алу жеткілікті. Сонымен, 
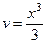. Бөліктеп интегралдау формуласын қолданып табамыз:
.
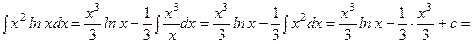
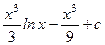Әдебиеттер: 4 нег. [203-237]; 15 қос. [167-182], [208-218].
Бақылау сұрақтары:
1. Экстремумның қажетті шартын айтыңыз.
2. Экстремумның жеткілікті шартын айтыңыз.
3. Анықталмаған интегралдың анықтамасын айтыңыз.
4. Анықталмаған интегралдың кестесін келтіріңіз.
