Неавтономные уравнения
Метод Пуанкаре предназначен для построения периодических решений нелинейных систем, дифференциальные уравнения которых содержат малый параметр m. При этом предполагается, что обращение в нуль малого параметра не понижает порядка системы.
Метод Пуанкаре базируется на двух положениях:
1) порождающая система, т.е. система, получающаяся из исходной при m =0, содержит периодические решения с некоторым периодом, частным случаем которых могут быть постоянные величины;
2) периодические решения исходной системы строятся при помощи подбора начальных данных всех входящих в систему неизвестных функций.
Начнем с решения следующей задачи: требуется найти периодическое решение периода T дифференциального уравнения:
. (7.1)
Заметим, что если решение уравнения (7.1) имеет период T, то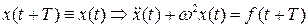 
, то есть функция f(t) обязана быть периодической с периодом T. Выполнив в (7.1) замену времени 
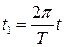и положив 
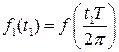, получим
.
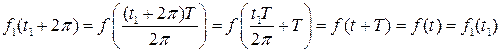То есть новая правая часть в новом времени будет 2 p -периодической функцией. Поэтому правую часть уравнения (2.9.1) можно без ограничения общности считать 2 p -периодической функцией.
Будем считать, что функция f(t) непрерывна и может быть разложена в сходящийся ряд Фурье
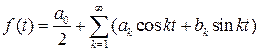. (7.2)
Пользуясь принципом суперпозиции, частное решение уравнения (7.1) будем искать в виде ряда
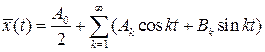. (7.3)
Дифференцируя ряд (7.3) почленно два раза и подставляя в (7.1), получим:
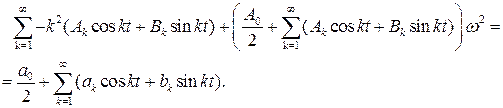
Приравнивая коэффициенты при одинаковых гармониках слева и справа в последней формуле, будем иметь
.
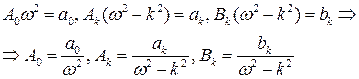Тогда
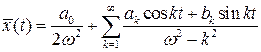(7.4)
Из предположения о непрерывности f(t) следует, что ряд (7.4) можно почленно дифференцировать. Поэтому ряд (7.4) есть решение уравнения (7.1), если только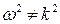 
ни для какого k. Если же число 
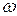целое (
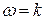), то соответствующее слагаемое в правой части (7.4) обращается в 
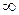, и периодическое решение не существует.
Полученный результат можно было легко предугадать, если вспомнить, что при 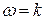линейное уравнение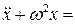 
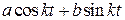имеет решение вида 
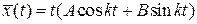, не являющееся периодическим.
Из приведенных рассуждений вытекает следующий вывод: если 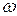не является целым числом, а f(t) – 2 p -периодическая функция, то уравнение (7.1) всегда имеет 2 p - периодическое решение, доставляемое формулой (7.4). Если же 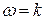– целое число, то 2 p - периодическое решение уравнения (7.1) существует лишь в том случае, когда в разложении функции f(t) в ряд Фурье отсутствуют «резонирующие члены» ak и bk, то есть если:
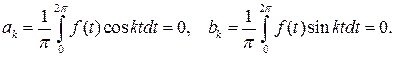(7.5)
Если 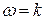и выполнено условие (7.5), то уравнение (7.1) имеет бесконечное число 2 p -периодических решений, которые даются формулой:
.
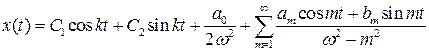Если же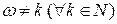 
, то уравнение (7.1) имеет единственное периодическое решение (7.4).
Пример 7.1. Существуют ли периодические решения уравнения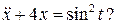 
Здесь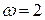 
– целое число.
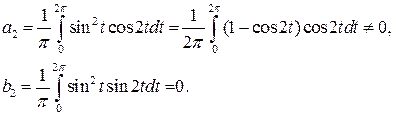
Так как условия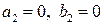 
не выполняются, то периодического решения у рассматриваемого уравнения нет.
Аналитическая зависимость решений от параметров
Рассмотрим задачу Коши для системы уравнений
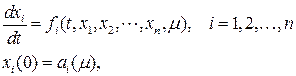(7.6)
где m является параметром.
Теорема 7.1. Если в системе (7.6) функции 
непрерывны по переменной t, а также функции и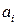 
аналитические функции параметра m в некоторой окрестности точки 
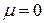, то решение 
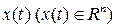этой системы разлагается в сходящийся при малых m ряд по степеням параметра m:
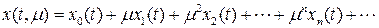(7.7)
Доказательство этой теоремы достаточно громоздко и здесь опущено.
Метод разложения решения по степеням малого параметра лежит в основе многих приемов исследования нелинейных колебаний с малой нелинейностью.
Рассмотрим следующую задачу: найти периодическое решение уравнения:
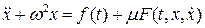(7.8)
с 2 p -периодическими по переменной t функциями f(t) и 
, считая, что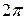 
-периодическое решение 
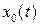порождающего уравнения:
(7.9)
существует и нам известно. Считая, что функция непрерывна по t и является аналитической по переменным x и 
, на основании приведенной выше теоремы, будем искать решение уравнения (7.8) в виде ряда (7.7).
Разложим функцию в ряд по степеням 
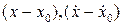в окрестности точки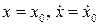 
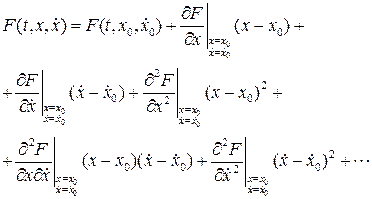(7.10)
Подставим в левую и правую части уравнения (7.8) вместо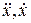 
и x ряд (7.7) и его соответствующие производные, а вместо выражение (7.10). Сравнивая коэффициенты при одинаковых степенях m в левой и правой частях полученного равенства, будем иметь:
(7.11)
Каждое следующее уравнение (7.11) будет содержать в правой части только известные функции, найденные из предыдущих уравнений. Поэтому все решения уравнений (7.11) могут быть последовательно найдены.
Если мы хотим найти 2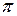 
-периодическое решение уравнения (7.8), то все члены ряда (7.7) должны быть 2 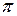-периодическими функциями. Значит каждое из уравнений (7.11) должно иметь 2 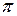-периодическое решение. Выясним, когда эти условия выполняются.
1) 
, где n – какое-либо целое число. Тогда 2 p -периодическое решение у порождающего уравнения (7.9) и всех остальных уравнений в (7.11) существует всегда. Все эти решения могут быть найдены так, как было описано выше.
2) 
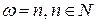. Тогда порождающее уравнение (7.9) имеет периодическое решение лишь при условии равенства нулю коэффициентов an и bn в разложении функции f(t) в ряд Фурье, то есть при выполнении условий:
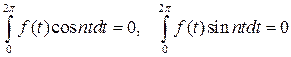. (7.12)
Если условия (7.12) выполнены, то порождающее уравнение имеет решение:
.
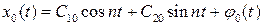Для определения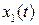 
имеем второе уравнение из (7.11). Оно будет иметь периодическое решение, если
. (7.13)
Уравнения (7.13) содержат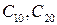 
, которые, вообще говоря, определяются из этой системы. Если 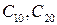удовлетворяют системе (7.13), то все решения второго уравнения в (7.11) будут периодическими с периодом 2 p и будут иметь вид:
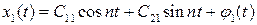. (7.14)
При этом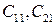 
опять определяются из двух условий, аналогичных (7.12) и (7.13), для третьего уравнения из (7.11). И так далее.
Как мы видим, в случае 2) (резонансный случай), вообще говоря, не любому 2 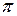-периодическому решению порождающего уравнения соответствует периодическое решение уравнения (7.8), задаваемое рядом (7.7), которое при 
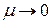сходится к решению порождающего уравнения. Существование подобного решение нужно доказать. Такое доказательство составляет содержание известной теоремы Пуанкаре. Но это доказательство очень громоздко и здесь не приводится.
Пример 7.2. Найти приближенно периодическое решение уравнения:
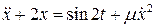, где m – малый параметр.
Решение будем искать в виде ряда по степеням малого параметра, то есть в виде
.
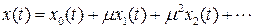Тогда
Подставим ряды в исходное уравнение
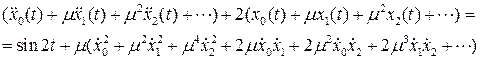
Приравняем коэффициенты при одинаковых степенях параметра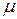 
в левой и правой частях последнего равенства:
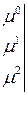
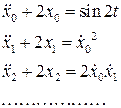(7.15)
Поскольку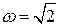 
, порождающее уравнение имеет единственное периодическое решение, которое будем искать в виде:
.
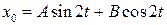После двукратного дифференцирования и подстановки в первое уравнение (7.15), получим:
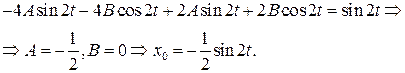
Для отыскания x 1 имеем уравнение
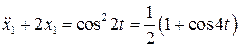
Будем искать x 1 в виде:
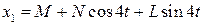
После двукратного дифференцирования и подстановки в уравнение получим:
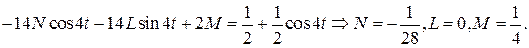
Итак,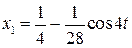 
.
Подставим найденные функции x 0 и x 1 в правую часть последнего уравнения (7.15). Тогда оно примет вид
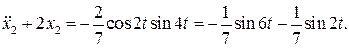(7.16)
Будем искать решение последнего уравнения в виде
.
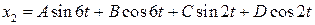После двукратного дифференцирования последнего выражения и подстановки в уравнение (7.16), находим
Итак, справедливо приближенное равенство
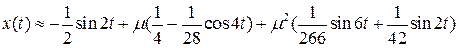. (7.17)
Используя пакет Mathcad, сравним полученное решение (7.17) с точным решением исходного уравнения на периоде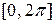 
. Для этого найдем для решения (7.17) значения x (0) и 
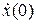, после чего найдем решение исходного уравнения с заданными начальными условиями, например, методом Рунге-Кутта. Результаты расчетов приведены ниже.
Исследуемое уравнение: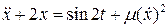 
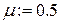
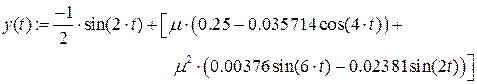
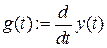
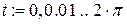
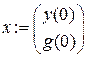
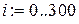
График для m=0.5 (жирная линия – решение методом Рунге-Кутта)
График для m=0.3 (жирная линия – решение методом Рунге-Кутта)
Автономные уравнения
Пусть задано уравнение, правая часть которого не зависит явно от t:
. (8.1)
Отсутствие t в правой части приводит к усложнению задачи, так как период искомого решения оказывается неизвестным. Он будет, вообще говоря, зависеть от параметра .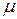
Для решения задачи в этом случае нужно преобразовать уравнение к новой независимой переменной так, чтобы по новой переменной уравнение уже имело постоянный период, а уже затем искать решение в виде ряда по параметру m.
Предварительно выполним в (8.1) замену времени, положив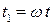 
. Тогда в новом времени уравнение примет вид:
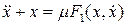, (8.2)
где производные и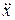 
вычислены по переменной t 1, а 
.
При m =0 порождающее уравнение 
имеет 2 p -периодическое решение вида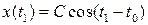 
, удовлетворяющее начальным условиям 
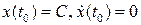. Периодические решения уравнения (8.2), если они существуют, будут иметь период 
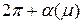, причем 
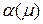– аналитическая функция m и 
при 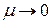. Пусть:
.
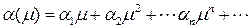Тогда:
.
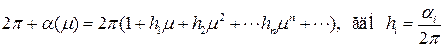Преобразуем уравнение (8.2) так, чтобы его решение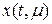 
имело постоянный период 2 p. Этого можно добиться заменой переменных:
(8.3)
Действительно, если t 1 меняется от 0 до 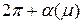, то t меняется от 0 до 2 p.
В новых переменных уравнение (8.2) приобретает вид:
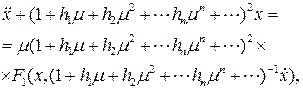(8.4)
где все производные вычислены по переменной t.
Периодическое решение уравнения (8.4) будем искать в виде ряда
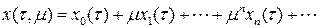, (8.5)
где все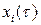 
– 2 p -периодические функции переменной t. Подставляя (8.5) в уравнение (8.4), получим:
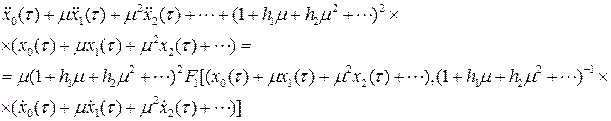
Приравнивая коэффициенты при одинаковых степенях параметра m в левой и правой частях последнего равенства, последовательно получим:
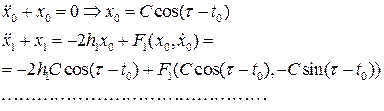(8.6)
Для того, чтобы второе уравнение в (8.6) имело периодическое решение, необходимо и достаточно, чтобы в его правой части отсутствовали резонирующие члены, то есть чтобы выполнялись условия:
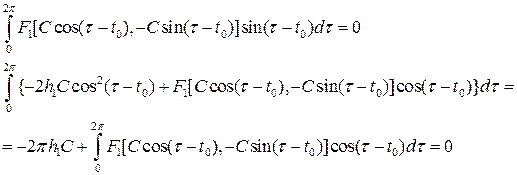(8.7)
Первое из этих уравнений дает возможность найти С (начальное условие периодического решения), а второе – найти h 1. Таким образом, будет приближенно определен период искомого периодического решения:
.
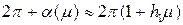Зная С и h 1, можно определить 
и, если это необходимо,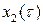 
, 
и так далее.
Пример 8.1. Определить решения порождающего уравнения, к которым при 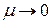приближаются периодические решения уравнения:
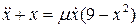(8.8)
Решения порождающего уравнения имеют вид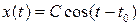 
. Для определения искомых значений С воспользуемся первым из уравнений (8.7):
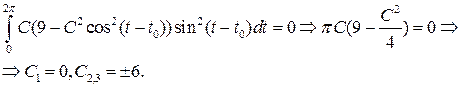
При С =0 получаем тривиальное решение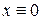 
порождающего уравнения, которое остается решением уравнения (8.8) при любом m.
При 
получаем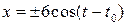 
.
Теорема Ляпунова и несколько практических замечаний
Теорема Ляпунова выделяет класс систем, у которых в некоторой окрестности состояния равновесия существует периодическое решение и дает метод отыскания этого решения.
Теорема 8.1. Если уравнение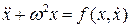 
обладает аналитическим первым интегралом 
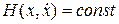, причем разложение 
в окрестности точки 
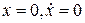начинается с членов второго порядка малости:
,
то все решения уравнения с достаточно малыми начальными условиями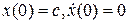 
есть периодические функции t. Каждое такое решение является аналитической функцией параметра с.
Сформулированная теорема позволяет искать период периодического решения уравнения
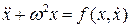
в виде
и вводить новое время по формуле
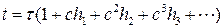, (8.9)
не вводя малого параметра m. При этом решение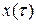 
следует искать в виде ряда
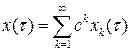(8.10)
Заметим, что если в уравнении не присутствует явно малый параметр и при этом в окрестности состояния равновесия выполнены условия теоремы Ляпунова, то для поиска периодического решения можно либо воспользоваться его разложимостью в ряд по начальным отклонениям с (формулой (8.10)), либо ввести малый параметр и использовать разложение по степеням малого параметра.
Пример 8.2. Найти приближенно периодическое решение уравнения Дуффинга
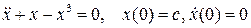. (8.11)
Для решения задачи можно ввести малый параметр:
.
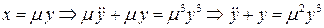Здесь m считаем малым. Теперь можно воспользоваться рассмотренной выше процедурой отыскания решения уравнения с малым параметром.
Заметим, что уравнение Дуффинга обладает аналитическим первым интегралом, для которого выполнены условия теоремы Ляпунова: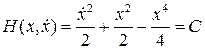 
. Поэтому данное уравнение можно решать, выполнив замену переменных (8.9) и отыскивая решение в виде ряда (8.10) по степеням начального возмущения с.
Выполним замену (8.9). Тогда
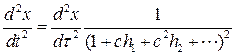
и уравнение примет вид
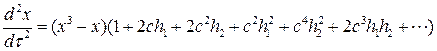(8.12)
Решение 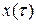будем искать в виде ряда (8.10). После двукратного дифференцирования и подстановки этого ряда в уравнение (8.12) будем иметь:
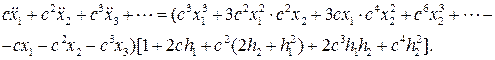
Приравнивая коэффициенты при одинаковых степенях с в обеих частях последнего равенства, получим
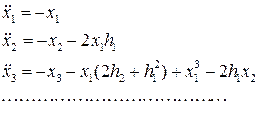(8.13)
Начальные условия для этих уравнений определяются так:
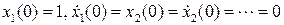(8.14)
Первое из уравнений (8.13) будет иметь общее решение вида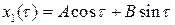 
. Из начальных условий находим, что 
. Итак,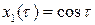 
. Второе уравнение тогда примет вид
.
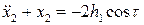Для того, чтобы это уравнение имело периодическое решение, в его правой части должны отсутствовать резонирующие члены. Это имеет место лишь при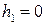 
. Таким образом, для 
получаем уравнение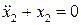 
, из которого, с учетом начальных условий (8.14), находим 
.
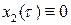Для получаем уравнение
.
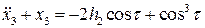Запишем условия отсутствия резонирующих членов в правой части этого уравнения:
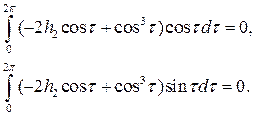
Второе из выписанных соотношений всегда выполнено, а первое дает условие
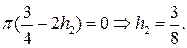
Итак, следует искать из уравнения:
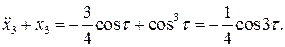
Отыскивая 2 p -периодическое решение этого уравнения, удовлетворяющее начальным условиям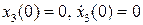 
, получим:
.
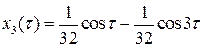Итак,
.
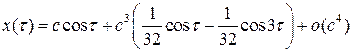Учитывая (8.9), окончательно получим
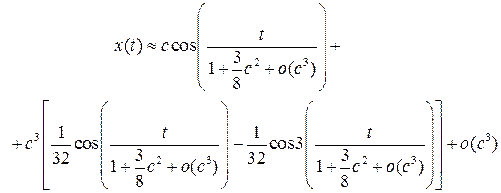
Пример 8.3. Найти приближенно периодическое решение уравнения:
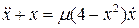
Выполним замену времени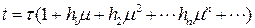 
. Тогда в новом времени исходное уравнение примет вид
(8.15)
Решение уравнения (8.15) будем искать в виде ряда (8.5). При этом будем искать решение с начальными условиями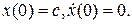 
Тогда:
.
Здесь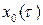 
– решение порождающего уравнения, то есть уравнения (8.15) при 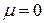. Поэтому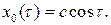 
Сравнивая коэффициенты при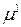 
в обеих частях равенства (8.15), найдем
Учитывая вид 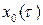, получим
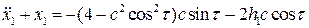(8.16)
Найдем условия существования периодического решения у уравнения (8.16). Для этого запишем соотношения (8.7). Чтобы записать это соотношение, нужно последовательно умножить правую часть уравнения (8.16) на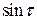 
и 
и, проинтегрировав полученные выражения, приравнять интегралы в нулю. В данном случае (убедиться в этом самостоятельно) результатом реализации описанных операций будут соотношения:
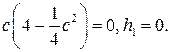
Таким образом, c = 0 или 
. Для c = 0 получаем тривиальное решение порождающего уравнения, которое остается решением исследуемого уравнения при любом m. Для c = 4 получаем периодическое решение порождающего уравнения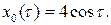 
Тогда для определения будем иметь уравнение
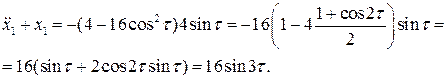
Итак, для получаем уравнение
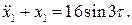(8.17)
Общее решение последнего уравнения имеет вид:
.
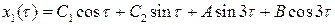Дважды дифференцируя это выражение и подставляя в (8.17), найдем значения А и В:
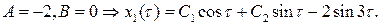
Используя начальное условие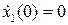 
, находим 
.
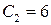Итак,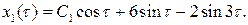 
Теперь, приравнивая коэффициенты при 
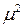слева и справа в (8.15), найдем (учитывая, что ):
.
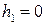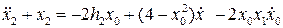Подставляя найденные выше значения 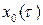и , получим
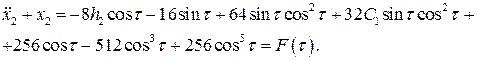
Запишем условия существования периодического решения для последнего уравнения
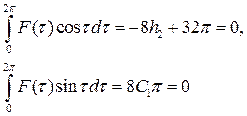
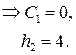
Теперь окончательно можем записать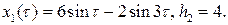 
Выпишем, наконец, приближенное решение исходного уравнения
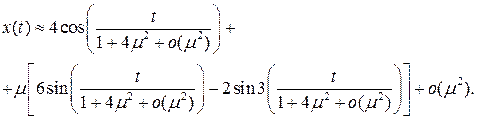
Используя пакет Mathcad, сравним полученное решение с решением исходного уравнения методом Рунге-Кутта на периоде [0, 2 p ].
Исследуемое уравнение: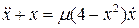
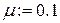
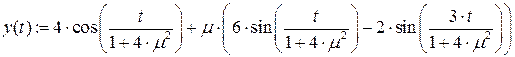
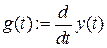
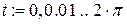
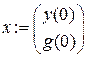
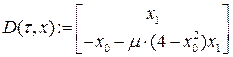
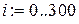
График для m=0.07 (жирная линия – решение методом Рунге-Кутта)
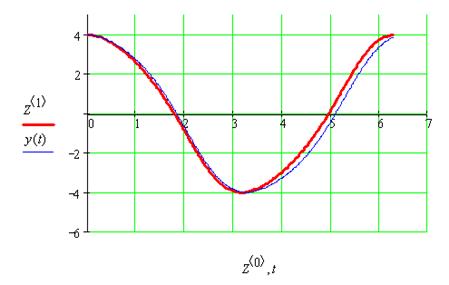
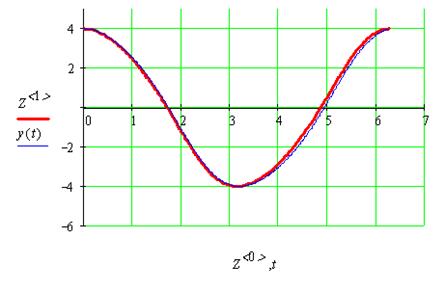
График для m=0.1 (жирная линия – решение методом Рунге-Кутта)
Задание 7
Методом Пуанкаре найти приближенно периодические решения данных уравнений.
1. 
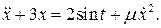
2. 
3. 
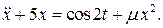
4. 
5. 
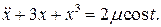
6. 
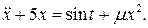
7. 
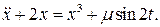
8. 
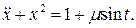
9. 
10. 
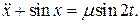
11. 
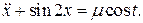
12. 
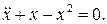
13. 
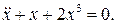
14. 
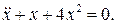
15. 
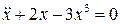
16. 
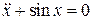
17. 
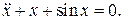
18. 
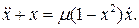
19. 
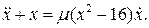
20. 
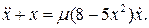
21. 
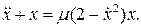
22. 
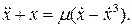
23. 
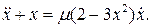
24. 
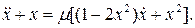
25. 
26. 
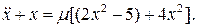
27. 
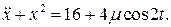
28. 
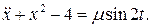
29. 
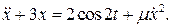
30. 
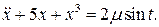
31. 
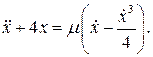
Библиографический список
1. Сборник задач по математике для втузов. В 4 частях. Ч. 2: Учебное пособие для втузов / Под общ. ред. А. В. Ефимова и А. С. Поспелова. – 4-е изд. перераб. и доп. – М. ФИЗМАТЛИТ, 2001. – 432 с.
2. Демидович Б.П. Лекции по математической теории устойчивости. – СПб. Лань, 2008. – 480 с. – (Учебники для вузов. Специальная литература).
3. Леонов Г.А., Буркин И.М., Шепелявый А.И. Частотные методы в теории нелинейных колебаний. Часть 1. Изд.-во Санкт-Петербургского университета, 1992. – 366 с.
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. – М. Либроком, 2009. – 240 с. – (Классический университетский учебник).
5. Понтрягин Л.С. Дифференциальные уравнения и их приложения – М. Едиториал УРСС, 2011. – 208 с.
6. Проскуряков А.П. Метод Пуанкаре в теории нелинейных колебаний. М. "Наука". 1977. – 256с.
7. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения. Практический курс. – М. Высшая школа, 2006.– 384 с.
8. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. – М. ФИЗМАТЛИТ, 2005. – 254 с. – (Классический университетский учебник).
9. Федорюк М.В. Обыкновенные дифференциальные уравнения. – М. Либроком, 2009. – 448 с. (Классический университетский учебник).
10. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – М. Либроком, 2013. – 240 с. (Классический учебник МГУ).
11. Хартман Ф. Обыкновенные дифференциальные уравнения. – М. Мир. 1970. –720 с.
