Линейным однородным дифференциальным уравнением первого порядка с частными производными называется уравнение вида
 , (3.1)
, (3.1)
где  – заданные функции, определенные в некоторой области
– заданные функции, определенные в некоторой области 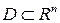 , а
, а  - искомая функция.
- искомая функция.
Линейным неоднородным уравнением первого порядка с частными производными называется уравнение вида
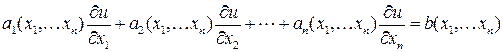 , (3.2)
, (3.2)
где  – заданные функции, определенные в некоторой области
– заданные функции, определенные в некоторой области 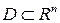 , а
, а  - искомая функция.
- искомая функция.
Квазилинейным уравнением первого порядка с частными производными называется уравнение вида
 , (3.3)
, (3.3)
где  – заданные функции, определенные в некоторой области
– заданные функции, определенные в некоторой области  , а
, а  - искомая функция.
- искомая функция.
Очевидно, что уравнения (3.1) и (3.2) являются частным случаем уравнения (3.3), поэтому ниже ставятся задачи и рассматриваются методы решения квазилинейных уравнений (3.3). Результаты для уравнений вида (3.1) и (3.2) получаются как следствия из них.
Система  обыкновенных дифференциальных уравнений
обыкновенных дифференциальных уравнений
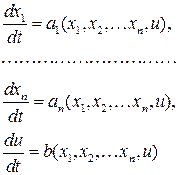 (3.4)
(3.4)
называется системой уравнений характеристик для уравнения (3.3), а ее фазовые кривые характеристиками уравнения (3.3). Исключив параметр  из системы (3.4), получим систему уравнений характеристик в симметричной форме
из системы (3.4), получим систему уравнений характеристик в симметричной форме
 . (3.5)
. (3.5)
Пусть найдено  независимых первых интегралов
независимых первых интегралов

 (3.6)
(3.6)
системы (3.5). Тогда общее решение уравнения (3) в неявном виде определяется равенством
 , (3.7)
, (3.7)
где  – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция.
Если функция  входит только в один из первых интегралов (6), например, в
входит только в один из первых интегралов (6), например, в  , то решение уравнения (3) может быть записано в виде
, то решение уравнения (3) может быть записано в виде  , где
, где  – произвольная дифференцируемая функция. Разрешив последнее уравнение относительно
– произвольная дифференцируемая функция. Разрешив последнее уравнение относительно  , получим общее решение в явном виде.
, получим общее решение в явном виде.
Точно также может быть найдено общее решение линейного неоднородного уравнения (2).
Общее решение линейного однородного уравнения (1) имеет вид
 , (3.8)
, (3.8)
где  – независимые первые интегралы системы уравнений характеристик, а
– независимые первые интегралы системы уравнений характеристик, а  – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция.
Пример 1. Найти общее решение уравнения
 . (3.9)
. (3.9)
Решение. Уравнение (3.9) – линейное однородное уравнение. Уравнение для характеристик в симметричной форме имеет вид  . Найдем независимые первые интегралы этого уравнения.
. Найдем независимые первые интегралы этого уравнения.


Согласно формуле (3.8), общее решение уравнения (9) имеет вид  , где
, где  – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция.
Пример 2. Найти общее решение уравнения
 . (3.10)
. (3.10)
Решение. Уравнение (10) – линейное неоднородное уравнение. Уравнение для характеристик в симметричной форме имеет вид
 . (3.11)
. (3.11)
Найдем независимые первые интегралы этого уравнения. Один первый интеграл находится из уравнения  и имеет вид
и имеет вид  . Для нахождения еще одного первого интеграла применим прием, позволяющий найти интегрируемую комбинацию. Воспользуемся следующим утверждением: если
. Для нахождения еще одного первого интеграла применим прием, позволяющий найти интегрируемую комбинацию. Воспользуемся следующим утверждением: если  , то при любых
, то при любых  справедливо равенство
справедливо равенство  . Используя это утверждение, из (3.11) получим
. Используя это утверждение, из (3.11) получим
 .
.
Поскольку функция  входит только в последний интеграл, решение уравнения может быть записано в виде
входит только в последний интеграл, решение уравнения может быть записано в виде  или
или  , где
, где  – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция.
Пример 3. Найти общее решение уравнения
 . (3.12)
. (3.12)
Решение. Уравнение (3.12) – квазилинейное. Уравнение для характеристик в симметричной форме имеет вид
 . (3.13)
. (3.13)
Найдем независимые первые интегралы этого уравнения. Один первый интеграл находится из уравнения  и имеет вид
и имеет вид  . Для нахождения еще одного первого интеграла применим описанный выше прием, позволяющий найти интегрируемую комбинацию. Из (3.13) последовательно получаем
. Для нахождения еще одного первого интеграла применим описанный выше прием, позволяющий найти интегрируемую комбинацию. Из (3.13) последовательно получаем

Согласно формуле (3.7), общее решение уравнения (3.12) в неявном виде определяется равенством  , где
, где  – некоторая дифференцируемая функция. Поскольку
– некоторая дифференцируемая функция. Поскольку  входит только в один первый интеграл, то решение мотет быть записано в виде
входит только в один первый интеграл, то решение мотет быть записано в виде  , или, окончательно
, или, окончательно  , где
, где  – некоторая дифференцируемая функция.
– некоторая дифференцируемая функция.
Задача Коши для уравнения с частными производными
Мы сформулируем задачу Коши для квазилинейного уравнения (3.3), ограничившись для простоты и наглядности случаем трех переменных. Для линейных уравнений (3.1) и (3.2), которые могут рассматривать как частный случай квазилинейного уравнения (3.3), задача Коши формулируется точно также.
Итак, рассмотрим квазилинейное уравнение
 (3.14)
(3.14)
и соответствующее уравнения характеристик
 . (3.15)
. (3.15)
Пусть пространственная кривая  задана параметрическими уравнениями
задана параметрическими уравнениями
 . (3.16)
. (3.16)
Обозначим через  проекцию этой кривой на плоскость
проекцию этой кривой на плоскость 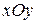 . Задача Коши для уравнения (3.14) ставится так: в окрестности кривой
. Задача Коши для уравнения (3.14) ставится так: в окрестности кривой  найти интегральную поверхность уравнения (3.3), проходящую через заданную кривую
найти интегральную поверхность уравнения (3.3), проходящую через заданную кривую  , т.е. найти такое решение уравнения (3.14), которое принимает заданные значения в точках кривой
, т.е. найти такое решение уравнения (3.14), которое принимает заданные значения в точках кривой  .
.
Задача Коши имеет единственное решение, если кривая  не является характеристикой уравнения (3.14). Если же
не является характеристикой уравнения (3.14). Если же  – характеристика, то задача Коши имеет бесконечно много решений.
– характеристика, то задача Коши имеет бесконечно много решений.
Пусть найдены два независимых первых интеграла системы (3.15)
 . (3.17)
. (3.17)
Выразив  через параметр
через параметр  из соотношений (3.16) и подставив эти выражения в (3.17), получим два соотношения вида
из соотношений (3.16) и подставив эти выражения в (3.17), получим два соотношения вида  . Исключив
. Исключив  из последних соотношений, получим выражение вида
из последних соотношений, получим выражение вида  . Подставив в это выражение вместо
. Подставив в это выражение вместо  и
и  левые части первых интегралов (3.17), получим искомое уравнение интегральной поверхности, которое и будет решением поставленной задачи Коши.
левые части первых интегралов (3.17), получим искомое уравнение интегральной поверхности, которое и будет решением поставленной задачи Коши.
Часто кривая  задается соотношениями
задается соотношениями 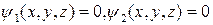 . В этом случае в качестве параметра на кривой можно выбрать
. В этом случае в качестве параметра на кривой можно выбрать  или
или  . Иначе говоря, для получения соотношения
. Иначе говоря, для получения соотношения  нужно исключить переменные
нужно исключить переменные  из системы уравнений
из системы уравнений
 . (3.18)
. (3.18)
Пример 4. Найти решение уравнения  , удовлетворяющее условию
, удовлетворяющее условию  при
при  .
.
Решение. Заданное уравнение является линейным неоднородным.Уравнения характеристик  . Из соотношения
. Из соотношения  получаем первый интеграл
получаем первый интеграл  . Сложив числители и знаменатели первых двух дробей и приравняв полученный результат к третьей дроби, получим
. Сложив числители и знаменатели первых двух дробей и приравняв полученный результат к третьей дроби, получим
 .
.
Найдены два независимых первых интеграла. Теперь запишем систему (3.18) для данной задачи:

 .
.
Подставив в последнее соотношение вместо  левые части выражений для первых интегралов, получим
левые части выражений для первых интегралов, получим  . Окончательно:
. Окончательно:  .
.
Пример 5. Найти поверхность, удовлетворяющую уравнению  и проходящую через линию
и проходящую через линию  .
.
Решение. Требуется найти частное решение квазилинейного уравнения. Уравнения характеристик имеют вид
 . (3.19)
. (3.19)
Из соотношения  получаем первый интеграл
получаем первый интеграл  . Умножим числитель и знаменатель первой дроби в (3.19) на
. Умножим числитель и знаменатель первой дроби в (3.19) на  , второй дроби – на
, второй дроби – на  и сложим числители и знаменатели полученных дробей с числителем и знаменателем третьей дроби в (3.19):
и сложим числители и знаменатели полученных дробей с числителем и знаменателем третьей дроби в (3.19):  . Приравняем полученную дробь к первой дроби в (3.19):
. Приравняем полученную дробь к первой дроби в (3.19):
 .
.
Итак, найдены два независимых первых интеграла. Теперь запишем систему (3.18) для данной задачи.

 .
.
Подставив в последнее соотношение вместо  левые части выражений для первых интегралов, будем иметь
левые части выражений для первых интегралов, будем иметь
 – уравнение искомой поверхности.
– уравнение искомой поверхности.
Задание 3
Найти общее решение уравнения:
1. 
2. 
3. 
4. 
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
Найти решения уравнения, удовлетворяющие заданным условиям:
11.  .
.
12.  .
.
13.  при
при  .
.
14.  при
при  .
.
15.  при
при  .
.
Найти поверхность, удовлетворяющую заданному уравнению и проходящую через заданную линию:
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
21.  .
.
22.  .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30. 
31.  .
.






