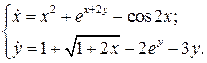Рассмотрим автономную систему
(5.1)
Пусть 
– положение равновесия системы (5.1). Будем предполагать, что функции 
дважды непрерывно дифференцируемы в некоторой окрестности точки 
.
Разложим каждую из функций 
в ряд Тейлора в окрестности точки a:
Здесь 
, , 
, 
.
Тогда система (5.1) будет иметь вид:
(5.2)
Отбросив в разложении (5.2) нелинейный член 
, квадратичный по 
, получим линейную систему
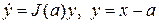. (5.3)
Система (5.3) – линеаризованная в окрестности точки система (5.1), или система линейного приближения (система первого приближения).
Теорема 5.1 (об устойчивости по первому приближению). Пусть функция 
дважды непрерывно дифференцируема в некоторой окрестности положения равновесия . Если вещественные части всех собственных значений матрицы Якоби 
отрицательны, то положение равновесия асимптотически устойчиво по Ляпунову и справедлива оценка
,
где 
– некоторые положительные постоянные, для всех 
достаточно близких к точке .
Замечание 5.1. Теорема 5.1 не охватывает так называемый критический случай, когда хотя бы одно собственное значение матрицы имеет вещественную часть равную нулю, а остальные ее собственные значения имеют отрицательные вещественные части. В этом случае на устойчивость решения начинают влиять квадратичные члены и исследование на устойчивость по первому приближению невозможно.
Теорема 5.2 (о неустойчивости по первому приближению). Пусть функция дважды непрерывно дифференцируема в некоторой окрестности положения равновесия . Если хотя бы одно собственное значение матрицы Якоби имеет положительную вещественную часть, то положение равновесия неустойчиво по Ляпунову.
Замечание 5.2. Теоремы об устойчивости и неустойчивости по первому приближению остаются справедливыми и в том случае, когда исходная система неавтономная, то есть имеет вид 
. При этом предполагается, что 
и система может быть представлена в виде 
.
Пример 5.1.
С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы:
Решение. Найдем матрицу Якоби системы:
.
Тогда 
.
Характеристическое уравнение полученной матрицы 
.
Один из корней характеристического уравнения 
. Два других корня имеют отрицательные вещественные части в следствие гурвицевости полинома 
.
Значит, нулевое решение рассматриваемой системы асимптотически устойчиво по Ляпунову.
Пример 5.2.
С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость все состояния равновесия системы
Решение. Для нахождения состояний равновесия решим систему уравнений
Итак, рассматриваемая система имеет следующие состояния равновесия: 
, 
и 
.
Найдем матрицу Якоби системы: 
.
Для точки матрица Якоби имеет вид 
. Ее собственные значения 
. Поэтому решение 
неустойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности начала координат.
Рис. 5.1. Фазовый портрет системы в окрестности точки
Для точки матрица Якоби имеет вид 
. Ее собственные значения 
. Поэтому решение 
асимптотически устойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности точки .
Рис. 5.2. Фазовый портрет системы в окрестности точки
Для точки матрица Якоби имеет вид 
. Ее собственные значения 
. Поэтому решение 
неустойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности точки .
Рис. 5.3. Фазовый портрет системы в окрестности точки
Пример 5.3.
С помощью теоремы об устойчивости по первому приближению найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение системы
Решение. Система первого приближения в данном случае имеет вид:
Составим соответствующее ей характеристическое уравнение:
Оба корня полученного уравнения будут иметь отрицательные вещественные части, если выполняются условия 
. Область асимптотической устойчивости рассматриваемой системы на плоскости 
изображена на расположенном ниже рисунке.
Рис. 5.4. Область асимптотической устойчивости в пространстве параметров
Результаты численного интегрирования рассматриваемой системы показывают, что при 
, 
точка покоя 
является устойчивой (устойчивый фокус), а при 
, 
- неустойчивой (точка покоя типа «седло»).
Рис. 5.5. Фазовый портрет системы при ,
Рис. 5.6. Фазовый портрет системы при ,
Пример 5.4.
Исследовать на устойчивость решение системы
Решение. Матрица системы первого приближения имеет вид:
.
Ее собственные значения 
. Поэтому нулевое решение рассматриваемой системы неустойчиво по Ляпунову.
Задание 5
С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы:
С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость все состояния равновесия системы
16. 
17. 
18. 
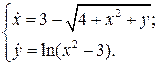
19. 
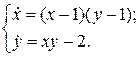
20. 
21. 
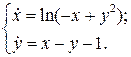
22. 
23. 
С помощью теоремы об устойчивости по первому приближению найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение системы:
24. 
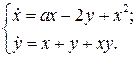
25. 
26. 
27. 
28. 
29. 
30. 
31. 
