Контрольна робота № 5 виконується учнями після вивчення наступних розділів програми:
· Диференціальні рівняння першого порядку.
· Диференціальні рівняння другого порядку, що дозволяють знизити порядок.
· Лінійні диференціальні рівняння другого порядку.
Завдання 1. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь першого порядку:
1)  2)
2)  3)
3) 
4)  5)
5) 
► 1) Маємо диференціальне рівняння з відокремленими змінними приведемо рівняння до вигляду

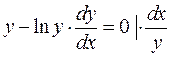

Інтегруємо 


Маємо загальний інтеграл диференціального рівняння 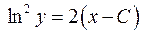 , С – довільна стала. ◄
, С – довільна стала. ◄
► 1) Маємо диференціальне рівняння з відокремленими змінними приведемо рівняння до вигляду


 ,
,
Інтегруємо  ,
,
 ,
,
 ,
,

 маємо
маємо
 – загальний розв’язок диференціального рівняння, С 1 – довільна стала. ◄
– загальний розв’язок диференціального рівняння, С 1 – довільна стала. ◄
► 3) Маємо однорідне диференціальне рівняння першого порядку
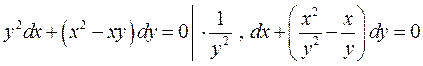
Виконаємо підстановку

Застосуємо підстановку 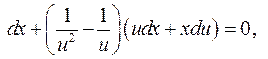
 ,
,

Інтегруємо 
 ,
,
Підставимо замість u її значення 
Маємо загальний інтеграл даного диференціального рівняння  ,
,
С – довільна стала. ◄
► 4) Маємо лінійне диференціальне рівняння першого порядку, це рівняння містить  у першому степені.
у першому степені.
Загальний розв’язок такого рівняння шукаємо за формулою:
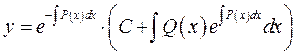

Маємо 
 ,
,
 ,
,

 – загальний розв’язок даного рівняння. ◄
– загальний розв’язок даного рівняння. ◄
► 5) Маємо рівняння Бернуллі, 
Розділимо рівняння  :
:
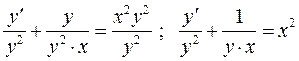 ,
,
Використаємо підстановку 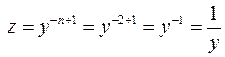 ,
,
Тоді  і рівняння прийме вигляд
і рівняння прийме вигляд

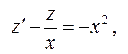
Це лінійне диференціальне рівняння відносно z,  .
.
За формулою  знаходимо
знаходимо

 ,
,
перейдемо до шуканої функції у. Підставимо замість z її значення  . Одержимо:
. Одержимо:
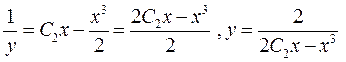 ,
,
 . ◄
. ◄
Завдання 2. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь другого порядку:
1)  ; 2)
; 2) 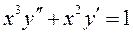 ; 3)
; 3) 
► 1) Рівняння другого порядку і не містить функції у та її похідної  . Введемо допоміжну змінну
. Введемо допоміжну змінну  . Тоді
. Тоді 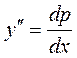 , маємо
, маємо
 , маємо диференціальне рівняння з відокремленими змінними, інтегруємо:
, маємо диференціальне рівняння з відокремленими змінними, інтегруємо:
 ,
,
підставимо замість  її значення
її значення  . Тоді отримаємо диференціальне рівняння відносно шуканої функції
. Тоді отримаємо диференціальне рівняння відносно шуканої функції
у  ,
,
інтегруємо 
 ,
,
 ;
;
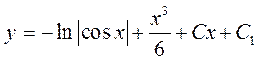 – загальний розв’язок рівняння. ◄
– загальний розв’язок рівняння. ◄
► 2) Рівняння другого порядку і не містить функції у,введемо допоміжну змінну  . Тоді
. Тоді 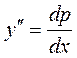 , маємо
, маємо
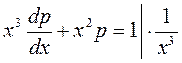 ,
,
Маємо лінійне диференціальне рівняння 1-го порядку  ,
,


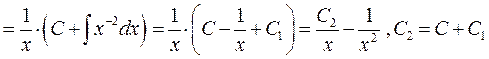 ,
,

підставимо замість  її значення
її значення  . Тоді отримаємо диференціальне рівняння відносно шуканої функції у
. Тоді отримаємо диференціальне рівняння відносно шуканої функції у
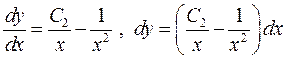
Інтегруємо 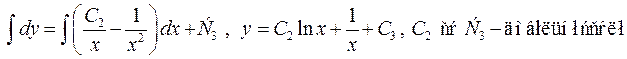
 – загальний розв’язок рівняння. ◄
– загальний розв’язок рівняння. ◄
► 3) Рівняння другого порядку і не містить явно змінну х. Використаємо допоміжну змінну 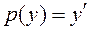 та
та  . Підставимо
. Підставимо
 та
та  в диференціальне рівняння, маємо
в диференціальне рівняння, маємо
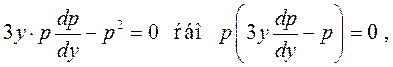
Звідси знаходимо:
а)  Тоді
Тоді  – один з розв’язків;
– один з розв’язків;
б)  – диференціальне рівняння з відокремленими змінними, інтегруємо:
– диференціальне рівняння з відокремленими змінними, інтегруємо:
 ,
,

підставимо замість  її значення
її значення  . Тоді отримаємо диференціальне рівняння відносно шуканої функції у:
. Тоді отримаємо диференціальне рівняння відносно шуканої функції у:

 – довільні сталі
– довільні сталі
 – загальний інтеграл заданого диференціального рівняння. ◄
– загальний інтеграл заданого диференціального рівняння. ◄
Завдання 3. Знайти загальний розв’язок (інтеграл) лінійних диференціальних рівнянь другого порядку:
1)  ; 2)
; 2)  ; 3)
; 3) 
Задані лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами, їх загальні розв’язки знайдемо з використанням відповідних характеристичних рівнянь.
► 1) Складаємо відповідне характеристичне рівняння шляхом заміни
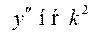 ,
,  і
і  . Маємо
. Маємо 
Знайдемо дискримінант цього рівняння за формулою 

Знайдемо корені цього рівняння 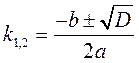
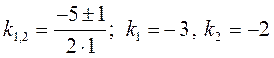 . Одержали два дійсних різних корені рівняння, тому загальним розв’язком диференціального рівняння буде
. Одержали два дійсних різних корені рівняння, тому загальним розв’язком диференціального рівняння буде
 – довільні сталі. ◄
– довільні сталі. ◄
►) Складаємо відповідне характеристичне рівняння шляхом заміни
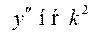 ,
,  і
і  . Маємо
. Маємо 
Знайдемо дискримінант цього рівняння 
Знайдемо корені цього рівняння  . Одержали комплексно спряжені корені, причому
. Одержали комплексно спряжені корені, причому  , тому загальним розв’язком диференціального рівняння буде
, тому загальним розв’язком диференціального рівняння буде
 – довільні сталі. ◄
– довільні сталі. ◄
► 3) Складаємо відповідне характеристичне рівняння шляхом заміни
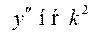 ,
,  і
і  . Маємо
. Маємо 
Знайдемо дискримінант цього рівняння 
Знайдемо корені цього рівняння  .Отже, характеристичне рівняння має два дійсних рівних корені
.Отже, характеристичне рівняння має два дійсних рівних корені  , тому
, тому
загальним розв’язком диференціального рівняння буде
 – довільні сталі. ◄
– довільні сталі. ◄
Контрольна робота № 6






