Контрольна робота № 3 виконується учнями після вивчення наступних розділів програми:
· Диференційованість функції однієї змінної.
· Основні теореми диференціального числення.
· Схема дослідження функції і побудова її графіка.
· Диференційованість функцій багатьох змінних.
· Дослідження функцій багатьох змінних на екстремум, умовний екстремум.
Розв’язування типових завдань
Завдання 1. Знайти похідні функцій: 1), 2) складної функції; 3), 4) неявної функції; 5), 6) параметрично заданої функції; 7), 8) використовуючи логарифмічне диференціювання.
1) 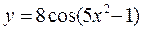 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 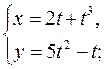 6)
6) 
7)  ; 8)
; 8) 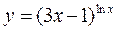
► 1) застосуємо правило диференціювання складної функції, тригонометричної функції та суми, маємо:

 ◄
◄
► 2) застосуємо правило диференціювання складної функції, оберненої тригонометричної функції та суми, маємо:

 ◄
◄
► 3) функція задана неявно, диференціюємо ліву та праву частини рівняння вважаючи, що 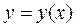 . Згідно з правилами диференціювання складної функції, маємо:
. Згідно з правилами диференціювання складної функції, маємо:

Звідси  ,
,
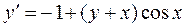 ◄
◄
► 4) функція задана неявно, диференціюємо ліву та праву частини рівняння вважаючи, що 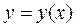 . Згідно з правилами диференціювання складної функції, показникової функції та добутку, маємо:
. Згідно з правилами диференціювання складної функції, показникової функції та добутку, маємо:

Звідси
 ,
,
 ◄
◄
► 5) функція задана параметрично, тому

 ◄
◄
► 6) функція задана параметрично, тому
 ◄
◄
► 7) Маємо складну показникові функцію, бо основа, і степінь залежать
від х
Прологарифмуємо задану функцію  .
.
Маємо  .
.
Диференціюємо обидві частини останньої рівності по х:
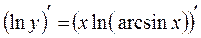 .
.
Звідси

Далі знаходимо  :
:
 ,
,
або
 ◄
◄
► 8) Маємо складну показникові функцію, бо основа, і степінь залежать
від х
Прологарифмуємо задану функцію 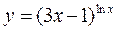 .
.
Маємо  .
.
Диференціюємо обидві частини останньої рівності по х:

Звідси 
Далі знаходимо  :
:
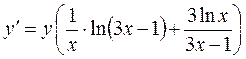 ,
,
або
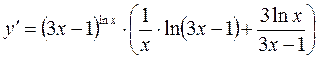 ◄
◄
Завдання 2. Знайти найбільше та найменше значення функції на заданому проміжку: 
► Область визначення функції – вся множина дійсних чисел  .
.
Знайдемо критичні точки першого роду заданої функції. Маємо:
 .
.
Похідна існує для всіх  , тому критичні точки одержимо із рівності
, тому критичні точки одержимо із рівності  .
.
Оскільки,  , то знайдемо значення функції при
, то знайдемо значення функції при  та
та  :
:
 ;
; 
 ;
;  .
.
Із отриманих значень функції обираємо найбільше значення  та найменше значення
та найменше значення  ◄
◄
Завдання 3. Знайти всі похідні другого порядку для заданих функцій:
а)  ; б)
; б) 
► а) Знайдемо частинні похідні першого порядку:
вважаючи у сталою, маємо  :
:
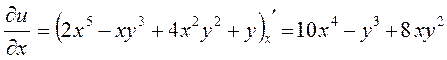 .
.
вважаючи х сталою, маємо 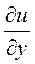 :
:
 .
.
Продиференціюємо ці рівності відповідно по х і по у.
Маємо
 ;
;
 .
.
Знайдемо мішані частинні похідні  та
та  :
:
 ,
,
 .
.
 ,
,
мішані похідні рівні, так як не залежать від порядку диференціювання. ◄
► б) Знайдемо частинні похідні першого порядку:
вважаючи у сталою, маємо  :
:

вважаючи х сталою, маємо 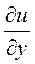 :
:

Тепер знайдемо частинні похідні другого порядку функції u, що входять до заданого рівняння:

 ;
;
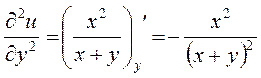
Знайдемо мішані частинні похідні  та
та  :
:
 ,
,
 ,
,
 ◄
◄
Завдання 4. Довести, що задана функція  z задовольняє задане рівняння:
z задовольняє задане рівняння:
а) 
б) 
► а) Знайдемо частинні похідні першого порядку:


Підставимо отримані частинні похідні в задане диференціальне рівняння, приходимо до тотожності
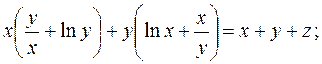

 ◄
◄
► б) Знайдемо частинні похідні функції  першого та другого порядків:
першого та другого порядків:
 ;
;  ,
,
 ,
,

Підставимо отримані частинні похідні в задане диференціальне рівняння, приходимо до тотожності
 ,
,
 ,
,
0 = 0 ◄
Завдання 5. Дослідити задану функцію на екстремум

► Функція визначена для усіх  . Знаходимо частинні похідні функції
. Знаходимо частинні похідні функції  z першого порядку:
z першого порядку:


Ці похідні існують при усіх  , тому критичними точками функції будуть лише ті точки, де
, тому критичними точками функції будуть лише ті точки, де  та
та  . Отже для знаходження критичних точок треба розв’язати систему:
. Отже для знаходження критичних точок треба розв’язати систему:

Отже, критичними точками заданої функції будуть точки:  та
та  .
.
Знайдемо частинні похідні другого порядку заданої функції.
 ;
;  ;
; 
Застосуємо достатню умову існування екстремуму функцій двох змінних до кожної критичної точки.
Тоді для точки  маємо:
маємо:
 ,
,  ;
; 
 М не є точкою екстремуму.
М не є точкою екстремуму.
Для точки  , маємо
, маємо
 ,
,  ,
, 
 .
.
Отже точка  – точка мінімуму.
– точка мінімуму.
Знайдемо значення  z в цій точці
z в цій точці  .
.
Контрольна робота № 4.






