Контрольна робота № 4 виконується учнями після вивчення наступних розділів програми:
· Невизначений інтеграл.
· Визначений інтеграл.
· Застосування визначених інтегралів.
Завдання 1. Знайти невизначені інтеграли. Результат перевірити диференціюванням:
1) 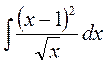 ; 2)
; 2) 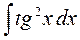 ; 3)
; 3) 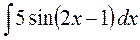 ; 4)
; 4) 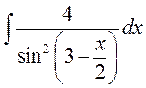 ;
;
5) 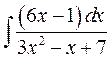 ; 6)
; 6) 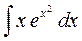 ; 7)
; 7) 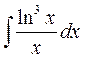 ; 8)
; 8) 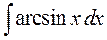 .
.
► 1) Виконаємо перетворення підінтегральної функції
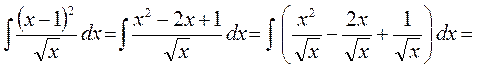
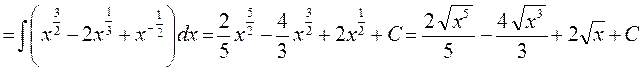 Перевірка результату диференціюванням
Перевірка результату диференціюванням
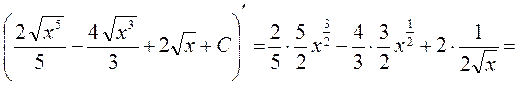
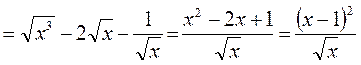 ◄
◄
► 2) Виконаємо перетворення підінтегральної функції
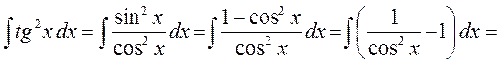
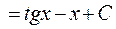
Перевірка результату диференціюванням
 ◄
◄
► 3) Використаємо метод безпосереднього інтегрування, аргумент підінтегральної функції відрізняється від аргументу табличного інтеграла постійним множником та постійним доданком.
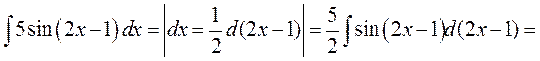
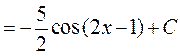 ;
;
Перевірка диференціюванням
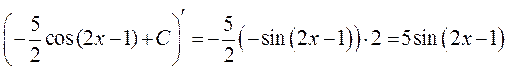 ◄
◄
► 4) Використаємо метод безпосереднього інтегрування, аргумент підінтегральної функції відрізняється від аргументу табличного інтеграла постійним множником та постійним доданком.
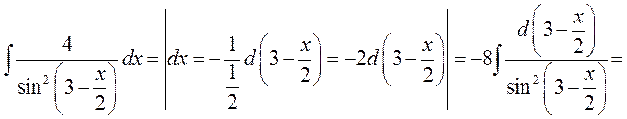
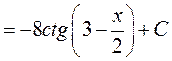 ;
;
Перевірка результату диференціюванням
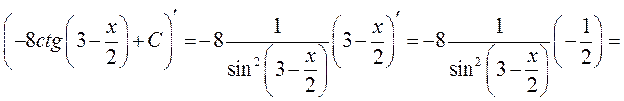
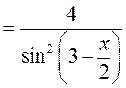 ◄
◄
►5) Використаємо метод заміни змінної, маємо
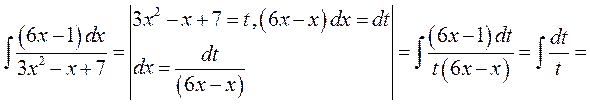
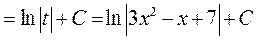 ;
;
Перевірка результату диференціюванням
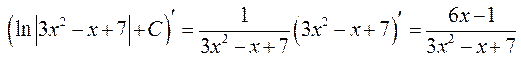 ◄
◄
► 6) Використаємо метод заміни змінної, маємо
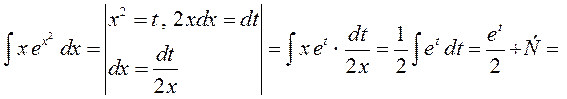
 ;
;
Перевірка результату диференціюванням
 ◄
◄
► 7) Використаємо метод заміни змінної, маємо
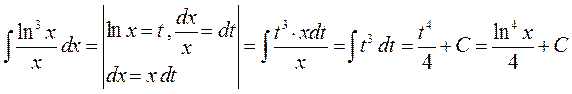
Перевірка результату диференціюванням
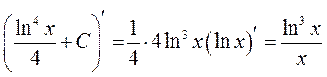 ◄
◄
► 8) Використаємо метод інтегрування частинами, маємо
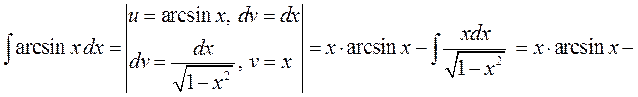
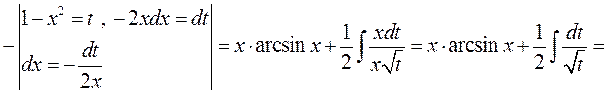
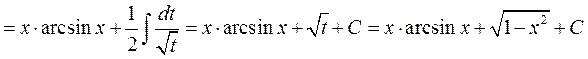 ;
;
Перевірка результату диференціюванням
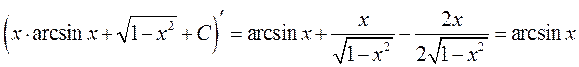 ◄
◄
Завдання 2. Обчислити визначені інтеграли:
1) 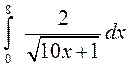 ; 2)
; 2) 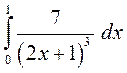 ; 3)
; 3) 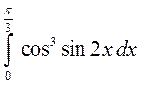 ;
;
4) 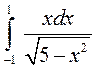 ; 5)
; 5) 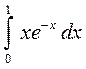 .
.
► 1) Заданий інтеграл будемо обчислювати за формулою Ньютона-Лейбніца. Використаємо метод безпосереднього інтегрування:
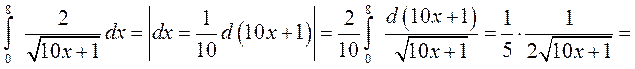
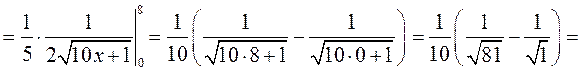
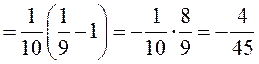 ◄
◄
► 2) Заданий інтеграл будемо обчислювати за формулою Ньютона-Лейбніца. Використаємо метод безпосереднього інтегрування:
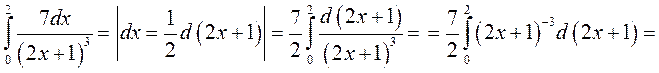
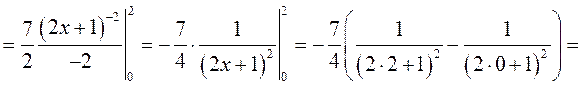
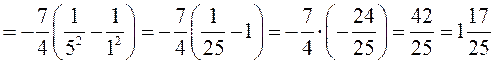 ◄
◄
► 3) Заданий інтеграл будемо обчислювати за формулою Ньютона-Лейбніца.
Використаємо метод заміни змінної:
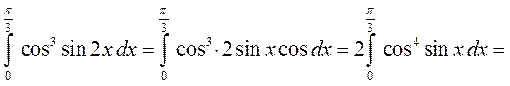
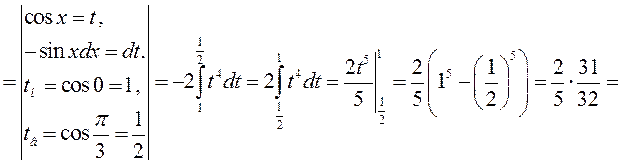
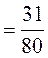 ◄
◄
► 4) Заданий інтеграл будемо обчислювати за формулою Ньютона-Лейбніца.
Використаємо метод заміни змінної:

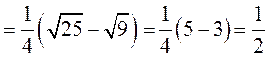 ◄
◄
►5) Заданий інтеграл будемо обчислювати за формулою Ньютона-Лейбніца.
Використаємо метод інтегрування частинами:
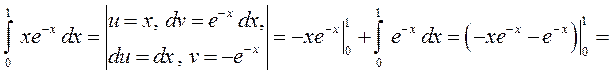
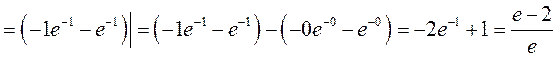 ◄
◄
Завдання 3. Обчислити площу фігури, обмеженої графіками функцій:
1) 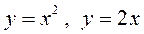 ; 2)
; 2)  .
.
► 1) Знайдемо координати точок перетину:
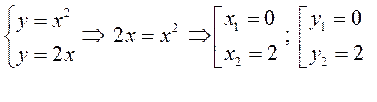
Будуємо графіки функцій:
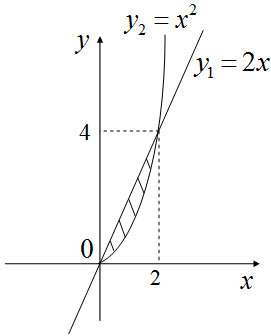
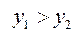 за формулою
за формулою 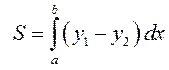 знаходимо площу криволінійної трапеції
знаходимо площу криволінійної трапеції
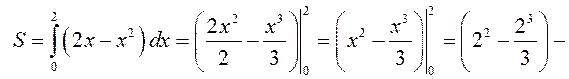
 ◄
◄
► 2) Знайдемо координати точок перетину та будуємо графіки функцій:

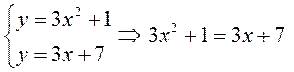
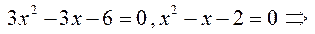
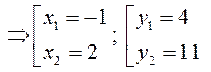
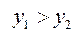 за формулою
за формулою 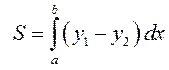 знаходимо площу криволінійної трапеції
знаходимо площу криволінійної трапеції
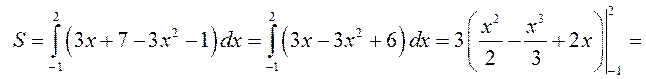
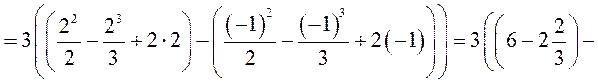
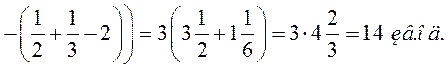 ◄
◄
Контрольна робота № 5






