1. Егер  функциясы
функциясы  кесіндісінде үзіліссіз болса, онда ол осы кесіндіде ақырлы (шенелген)
кесіндісінде үзіліссіз болса, онда ол осы кесіндіде ақырлы (шенелген)
2. Вейерштрасс теоремасы Егер  функциясы
функциясы  кесіндісінде үзіліссіз болса, онда ол осы кесіндіде өзінің ең кіші және ең үлкен мәндерін қабылдайды.
кесіндісінде үзіліссіз болса, онда ол осы кесіндіде өзінің ең кіші және ең үлкен мәндерін қабылдайды.
3. Больцано-Коши теоремасы Егер  функциясы
функциясы  кесіндісінде үзіліссіз және және
кесіндісінде үзіліссіз және және  ,
,  нүктелеріндегі мәндері әртүрлі таңбалар қабылдаса (
нүктелеріндегі мәндері әртүрлі таңбалар қабылдаса (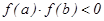 ), онда
), онда  теңдігі орындалатындай
теңдігі орындалатындай  кесіндісінің ең болмағанда
кесіндісінің ең болмағанда  бір нүктесі бар.
бір нүктесі бар.
Әдебиеттер: 1 нег.[159-162], [164-169], [191-211], 11 қос. [335-358].
Бақылау сұрақтар:
1. Бірінші тамаша шек.
2. е санының анықтамасын келтіріңіз (екінші тамаша шек).
3. Функцияның нүктедегі үзіліссіздігінің анықтамасын беріңіз.
4. Қандай нүктелер функцияның үзіліс нүктелері деп аталады?
Дәріс.
Дәріс тақырыбы:Бір айнымалы функциялардың дифференциалдық есептеулері.
Дәріс жоспары:
§ Функцияның туындысы.
§ Дифференциалдаудың негізгі ережелері.
§ Күрделі функцияны дифференциалдау.
§ Кері функцияны дифференциалдау.
§ Функция дифференциалы.
§ Әдебиеттер.
§ Бақылау сұрақтары.
Айталық,  функциясы
функциясы  нүктесінде және оның маңайында анықталған болсын.
нүктесінде және оның маңайында анықталған болсын.
Анықтама. Аргумент  -тің
-тің  нүктесіндегі өсімшесі деп
нүктесіндегі өсімшесі деп 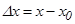 айырмасын атайды.
айырмасын атайды.
Анықтама.  функцияның
функцияның  нүктесіндегі өсімшесі деп
нүктесіндегі өсімшесі деп  айырмасын айтады.
айырмасын айтады.
Анықтама. Егер  функциясы
функциясы  нүктесінің маңайында анықталған және
нүктесінің маңайында анықталған және  болса, онда ол
болса, онда ол  нүктесінде үзіліссіз деп аталады. Шындығында да
нүктесінде үзіліссіз деп аталады. Шындығында да 

 .
.
Анықтама.  функциясының
функциясының  нүктесіндегі туындысы деп
нүктесіндегі туындысы деп
 ақырлы шегін айтады.
ақырлы шегін айтады.
Бұл туынды мына символдардың бірімен белгіленеді:  .
.
Егер  функциясының
функциясының  интервалының әрбір нүктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
интервалының әрбір нүктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
Теорема. Егер  функциясы
функциясы  нүктесінде дифференциалданатын функция болса, онда ол бұл нүктеде үзіліссіз болады.
нүктесінде дифференциалданатын функция болса, онда ол бұл нүктеде үзіліссіз болады.
Ескерту: теорема керісінше дұрыс емес.
Туындының геометриялық мағанасы. Туындының геометриялық мағынасы: туындысы функциясының графигіне нүктесінде жүргізілген жанаманың бұрыштық коэффициенті болады. Осы жанаманың теңдеуін былай жазады:.Туындының механикалық мағынасы. Егер айнымалысын уақыт деп есептеп, - функциясы дененің жүрген жолын сипаттаса, онда дененің уақытындағы жылдамдығын білдіреді.
Дифференциалдаудың негізгі ережелері. Туындының анықтамасын пайдаланып, кейбір элементар (қарапайым) функциялардың туындыларын есептейміз.
1. Көрсеткішті функция 
 . Дербес жағдайда
. Дербес жағдайда 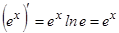 .
.
2. Тригонометриялық функциялар  .
.

 Дәл осылай
Дәл осылай  .
.
2. Дәрежелік функция  .
. 
Дербес жағдайда,  .
.
Теорема 1. (қосындыны, көбейтіндіні және қатынасты дифференциалдау ережелері). Егер  және
және  дифференцианалданатын болса, онда бұл функциялардың қосындысы, көбейтіндісі және қатынасы да (қатынастың бөлімі
дифференцианалданатын болса, онда бұл функциялардың қосындысы, көбейтіндісі және қатынасы да (қатынастың бөлімі  ) осы нүктеде дифференцианалданады және мына формулалар орынды:
) осы нүктеде дифференцианалданады және мына формулалар орынды:
1.  2.
2.  3.
3.  .
.
Күрделі функцияның туындысы.  функциялары үзіліссіз және дифференциалданатын функциялар болсын. Сонда күрделі
функциялары үзіліссіз және дифференциалданатын функциялар болсын. Сонда күрделі  функциясының туындысы:
функциясының туындысы:  . Сонымен
. Сонымен  .
.
1-мысал. 
 туындысын табу керек. Функцияны былай жазамыз
туындысын табу керек. Функцияны былай жазамыз  , мұндағы
, мұндағы  . Сондықтан
. Сондықтан  .
.
2-мысал.  туындысын табу керек.
туындысын табу керек.  .
.
Кері функцияның туындысы.  және оған кері
және оған кері  функциялары
функциялары  кесіндісінде үзіліссіз және дифференциалданатын болсын. Сонда кері функцияның туындысы:
кесіндісінде үзіліссіз және дифференциалданатын болсын. Сонда кері функцияның туындысы: 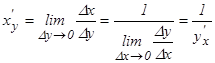 . Сонымен
. Сонымен  болады.
болады.
3-мысал.  .
.
Мұнда  .
.  .
.
4-мысал.  .
.
Негізгі элементар функциялар туындыларының кестесі


| 
|
Осы кесте мен туындыны есептеу ережелерінің жәрдемімен кез келген функциялардың туындысын табуға болады.
Параметр арқылы берілген функцияның туындысы.  функциясын кейде параметрлік түрде жазған ыңғайлы болады
функциясын кейде параметрлік түрде жазған ыңғайлы болады 
Онда  . Сонымен параметр арқылы берілген функцияның туындысы:
. Сонымен параметр арқылы берілген функцияның туындысы: 
5-мысал. 
 ,
,  табу керек. Шешімі:
табу керек. Шешімі: 
Функцияның дифференциалы.  функциясының шектелген туындысы бар болсын, онда:
функциясының шектелген туындысы бар болсын, онда:  , демек
, демек 
 шексіз аз шама.
шексіз аз шама.
Онда функцияның өсімшесі былай жазылады:  . Осы теңдікте екінші қосылғыш
. Осы теңдікте екінші қосылғыш  ,
,  ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш
ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш  ке эквивалентті шама болады.
ке эквивалентті шама болады.
Анықтама. Функцияның туындысының аргументтің өсімшесіне көбейтіндісін дифференциал деп атайды және мына түрде жазады:  . Дербес жағдайда, егер
. Дербес жағдайда, егер  болса, онда
болса, онда  , осыдан
, осыдан  және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:
және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:  . Осыдан
. Осыдан  , яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
, яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
Дифференциалды есептеу ережесі. Айталық  және
және  дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
1)  , мұндағы с – сан.
, мұндағы с – сан.
2)  ,
,
3)  , егер
, егер  .
.
4) Егер  функциясы
функциясы  нүктесінде дифференциалданатын, ал
нүктесінде дифференциалданатын, ал 
 нүктесінде дифференциалданатын болса, онда
нүктесінде дифференциалданатын болса, онда  күрделі функция үшін,
күрделі функция үшін,  . Бұл ережені бірінші дифференциал формасының инварианттығы деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,
. Бұл ережені бірінші дифференциал формасының инварианттығы деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,  функциясы дифференциалданатын болсын, онда оның өсімшесі:
функциясы дифференциалданатын болсын, онда оның өсімшесі:
 , осыдан
, осыдан  .
.
Егер  нүктесінде функцияның мәні берілсе, онда:
нүктесінде функцияның мәні берілсе, онда:  .
.
6-мысал.  -ты жуықтап есепте.
-ты жуықтап есепте. 
 .
.
Әдебиеттер: 1 нег.[211-238], 11 қос. [359-375], [377-385].
Бақылау сұрақтар:
1. Туындының анықтамасын келтіріңіз. Оның механикалық және геометриялық мағынасы қандай?
2. Кері функцияның туындысы туралы теорема. Кері тригонометриялық функцияларды дифференциалдау формулаларын жазыңыз.
3. Функцияның дифференциалының анықтамасын келтіріңіз. Жуықтап есептеуде
дифференциалдың қолдануы неге негізделген?
Дәріс.
Дәріс тақырыбы: Жоғарғы ретті туындылар мен дифференциалдар.
Дәріс жоспары:
§ Жоғарғы ретті туындылар.
§ Жоғары ретті дифференциалдар.
§ Дифференциалдыесептеуформулалары.
§ Дифференциалдық есептеудің негізгі теоремалары.
§ Лопиталь ережесі.
§ Әдебиеттер.
§ Бақылау сұрақтары.
 берілген
берілген  функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.
функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.
Анықтама. Функцияның  –ші ретті туындысы деп оның (
–ші ретті туындысы деп оның ( -1)-ші туындысының туындысын айтады
-1)-ші туындысының туындысын айтады  ,
,  =1,2,3,…, егер олар бар болса, онда
=1,2,3,…, егер олар бар болса, онда  функциясы
функциясы  -рет дифференциалданатын функция деп аталады.
-рет дифференциалданатын функция деп аталады.
Мысал.  функциясы берілген. Бірінші туындысы
функциясы берілген. Бірінші туындысы 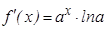 , екінші туындысы
, екінші туындысы  , үшінші туындысы
, үшінші туындысы  . Демек,
. Демек,  ,
,  . Егер
. Егер  және
және  функциялары
функциялары  –рет дифференциалданатын болса, онда (
–рет дифференциалданатын болса, онда ( ), мына ережелер орынды:
), мына ережелер орынды:  ,
,  .
.
2. Лейбниц формуласы:

 ;
;  .
.
Айталық  функциясы
функциясы  –рет дифференциалданатын болсын.
–рет дифференциалданатын болсын.
Анықтама. Функцияның  –ші дифференциалы деп оның (
–ші дифференциалы деп оның ( )–ші ретті дифференциалының дифференциалын айтады:
)–ші ретті дифференциалының дифференциалын айтады:  .
.
Дифференциалды есептеу формулаларын келтірейік:
 ,
,
 ,
,
 ,
,
… … … … … … … … … … … … … … …
 .
.  –шы ретті дифференциалдар үшін мына ережелер орынды:
–шы ретті дифференциалдар үшін мына ережелер орынды:
1) 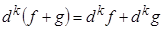 ,
,  .
.
2)  ,
,  .
.
Ескерту: Жоғарғы ретті  дифференциал формасы инвариантты емес.
дифференциал формасы инвариантты емес.






