 (6.6)
(6.6)
Теорема. (6.6) теңдеуі әрқашан не шеңберді (егер  ), не эллипсті (егер
), не эллипсті (егер  ), не гиперболаны (егер
), не гиперболаны (егер 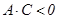 ), не параболаны (егер
), не параболаны (егер  ) анықтайды. Бұл жағдайларда эллипс (шеңбер) нүктеге немесе жорымал эллипске (шеңберге), гипербола қиылысатын түзулердің жұбына, парабола параллель түзулердің жұбына айналуы мүмкін.
) анықтайды. Бұл жағдайларда эллипс (шеңбер) нүктеге немесе жорымал эллипске (шеңберге), гипербола қиылысатын түзулердің жұбына, парабола параллель түзулердің жұбына айналуы мүмкін.
1-мысал. 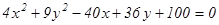 теңдеуін канондық түрге келтіру керек.
теңдеуін канондық түрге келтіру керек.
 эллипстің теңдеуі.
эллипстің теңдеуі.


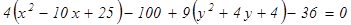




 . Осыдан
. Осыдан  деп белгілесек
деп белгілесек  -эллипстің канондық теңдеуі, Бұл жүйенің басы
-эллипстің канондық теңдеуі, Бұл жүйенің басы  нүктесінде орналасқан.
нүктесінде орналасқан.
Екінші ретті беттер
1. Сфера. Берілген нүктеден бірдей қашықтықта орналасқан кеңістіктегі нүктелердің геометриялық орындарын сфералық немесе шар беті дейді. Оның канондық теңдеуі:

мұндағы  сфераның центрі. Егер сфераның центрі
сфераның центрі. Егер сфераның центрі  нүктесінде болса,
нүктесінде болса,
онда оның теңдеуі мына түрде болады: 
2. Цилиндр. Цилиндр перпендикулярлық қимасындағы сызықтың түріне қарай дөңгелек, эллипстік, гиперболалық және параболалық цилиндрлер деп төртке бөлінеді.Осыған сәйкес төменгі теңдеулермен анықталады:  ,
,  ,
,  ,
,  .
.
Бұл теңдеулер жазықтықта шеңберді, эллипсті, гиперболаны және параболаны кескіндейді, ал кеңістікте цилиндрлердің теңдеулері. Бұл цилиндрлердің жасаушылары  өсіне параллель болады.
өсіне параллель болады.
Kонус
Kонус деп берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалысынан шығатын геометриялық бетті айтады. Оның теңдеуі:  . Бұл конустың бағыттаушысы
. Бұл конустың бағыттаушысы  эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтеді. Егер конустың перпендикулярлық қимасы шеңбер болса, онда оның теңдеуі:
эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтеді. Егер конустың перпендикулярлық қимасы шеңбер болса, онда оның теңдеуі: 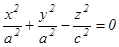 болады; егер
болады; егер  болса, онда конустың теңдеуі
болса, онда конустың теңдеуі  болады.
болады.
4. Айналу беттері. Егер кеңістікте бір сызық берілген өсті айналса, оның айналуынан бет пайда болады. Айналушы сызықтың формасына байланысты бет әр түрлі болады. Мысалы, шеңбер өзінің диаметрі бойынша айналса, сфералық бет шығады, ал координаталар басынан өтетін түзу Oz өсін айналса, дөңгелек конус пайда болады. Сызықтың айналатын өсін айналу өсі, ал пайда болған бетті айналу беті дейді.
5. Эллипсоидтың теңдеуі:  , мұндағы
, мұндағы  жарты өстер.Бұл үш өсті эллипсодтың теңдеуі болады.
жарты өстер.Бұл үш өсті эллипсодтың теңдеуі болады.  эллипсін
эллипсін  өсімен айналдырғаннан шыққан бетті айналу эллипсоиды деп атайды. Оның теңдеуі:
өсімен айналдырғаннан шыққан бетті айналу эллипсоиды деп атайды. Оның теңдеуі: 
6. Бір қуысты гиперболоид:  .
.
 гиперболасын
гиперболасын  өсінен айналдырсақ бір қуысты гиперболоид деп аталатын айналу беті шығады, оның теңдеуі:
өсінен айналдырсақ бір қуысты гиперболоид деп аталатын айналу беті шығады, оның теңдеуі:  .
.
7. Екі қуысты гиперболоид: 
8. Эллипстік параболоид 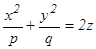 , мұндағы
, мұндағы  .
.
9. Гиперболалық параболоид  , мұндағы
, мұндағы  .
.
Әдебиеттер: 1 нег.[100-126], 11 қос. [41-58], [198-210].
Бақылау сұрақтар:
1. Эллипстің анықтамасы.
2. Эллипстің, гиперболаның, параболаның канондық теңдеулерін көрсетіңіз.
3. Гиперболаның асимптотасының теңдеуін жазыңыз.
4. Екінші ретті беттерді атаңыз.
5. Екінші ретті беттерді параллельдік қима әдісімен қалай зерттейді?
Дәріс.
Дәрістақырыбы: Тізбектің және функцияның шектері
Дәрісжоспары:
§ Функция.
§ Функцияныңнегізгіқасиеттері.
§ Функцияның нүктедегі шегі.
§ Функцияның ақырсыздықтағы шегі.
§ Шексіз аз және шексіз үлкен функциялар.
§ Әдебиеттер.
§ Бақылау сұрақтары.
Анықтама.  және
және  бос емес сандар жиындары болсын. Егер
бос емес сандар жиындары болсын. Егер  жиынының кез келген
жиынының кез келген  элементіне белгілі бір заңдылықпен
элементіне белгілі бір заңдылықпен  жиынының бір
жиынының бір  элементі сәйкес келетін болса, онда
элементі сәйкес келетін болса, онда  жиынында
жиынында  функциясы берілді дейді. Мұндай жағдайда
функциясы берілді дейді. Мұндай жағдайда  ті тәуелсіз шама (аргумент), ал
ті тәуелсіз шама (аргумент), ал  ті тәуелді шама деп атайды.
ті тәуелді шама деп атайды.  әрпі
әрпі  пен
пен  жиындарының арасында сәйкестік заңдылықты береді.
жиындарының арасында сәйкестік заңдылықты береді.  жиыны функцияның анықталу облысы, ал
жиыны функцияның анықталу облысы, ал  жиыны функция мәндерінің жиыны деп аталады.
жиыны функция мәндерінің жиыны деп аталады.
Функцияның үш түрлі жолмен беріледі:
а)Аналитикалық тәсілмен;
б) Таблицалық, яғни мәндер тәсілімен;
в) Графиктік тәсілмен






