нүктесі түзудің бойында жатсын және ол түзу 
векторына параллель болсын. Түзудің бойынан кез келген 
нүктесін аламыз. Сонда, 
. 
векторы түзудің бойында жатқандықтан || 
болады. Сондықтан түзудің канондық теңдеуі:
(5.8)
Мұндағы - бағыттаушы вектор деп аталады.
3. Түзудің параметрлік теңдеуі. (5.7) теңдеуіндегі әр теңдікті 
ға теңеп, мына теңдеуді аламыз:
(5.9)
4. Түзудің жалпы теңдеуі. Өзара параллель емес екі жазықтық жалпы теңдеулерімен берілсін:
, 
(5.10)
Сонда бұл жазықтықтар бір түзудің бойымен қиылысады. Ендеше осы екі жазықтықтың қиылысқан түзуінің бойындағы кез келген нүктенің координаттары екі жазықтықтың да теңдеуін қанағаттандырады. Сондықтан осы екі теңдеулер жүйесін түзудің жалпы теңдеуі дейді.
5. Екі түзудің арасындағы бұрыш. Екі түзу канондық теңдеулерімен берілсін:
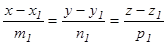және 
Екі түзудің арасындағы бұрыш, сол түзулердің бағыттаушы векторларының арасындағы бұрышқа тең (
, 
):
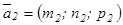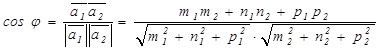(5.10)
Егер түзулер өзара параллель болса, онда 
|| 
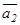болады. Түзулердің параллелдік шарты:
, егер түзулер өзара перпендикуляр болса, онда 
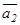болады. Түзулердің перпендикулярлық шарты: 
болады.
Түзу мен жазықтық. Жалпы теңдеуімен берілген жазықтық 
пен канондық теңдеуімен түзудің арасындағы бұрышты табу керек.
Түзу мен жазықтықтың арасындағы бұрыш деп, осы түзу мен оның жазықтыққа түсірілген проекциясының арасындағы сыбайлас бұрыштың біреуін айтады. Түзу мен жазықтықтың арасындағы бұрыштың синусы мына формуламен есептелінеді:
(5.11)
Түзу мен жазықтықтың параллелдік белгісі: 
. Түзу мен жазықтықтың перпендикулярлық белгісі: 
1-мысал. 
түзуі мен 
жазықтығының арасындағы бұрыштың синусы мен қиылысу нүктесін табу керек. 
, ал 
болғандықтан 
. Қиылысу нүктесін табу үшін түзу мен жазықтықтың теңдеулер жүйесін шешеміз. Сонда 
. Осыдан 
, яғни 
.
Әдебиеттер: 1 нег.[73-100], 11 қос. [181-198].
Бақылау сұрақтар:
1. Жазықтықтың жалпы теңдеуін көрсетіңіз.
2. Жазықтықтың жалпы теңдеуіндегі 
коэффициенттері нені білдіреді?
3. Түзудің канондық теңдеуіндегі 
нені білдіреді?
4. Түзу мен жазықтықтың арасындағы бұрышты қалай анықтайды?
5. Түзу мен жазықтықтың қиылысу нүктесін қалай анықтайды?
Дәріс.
Дәріс тақырыбы: Екінші ретті қисықтар мен беттер.
Дәрісжоспары:
§ Екінші ретті қисықтар (шеңбер,эллипс, гипербола, парабола).
§ Екінші ретті қисықтардыңжалпытеңдеуі.
§ Екінші реттібеттер (сфера, цилиндр, конус, айналу беттері, эллипсоид, гиперболоид, параболоид)
§ Әдебиеттер.
§ Бақылаусұрақтары..
Шеңбер
Анықтама. Центр деп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын шеңбер деп атайды.
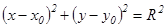(6.1)
(6.1) – теңдеуі центрі С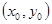 
нүктесінде жатқан радиусы R -ге тең шеңбердің теңдеуі.
Егер шеңбердің центрі С координаттардың бас нүктесінде жатса, яғни 
болса, онда (6.1) мына түрге келеді:
(6.2)
Эллипс
Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.
Анықтама бойынша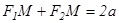 
, мұндағы 
және 
- фокустар деп аталатын берілген нүктелер, 
-эллипстің бойындағы кез келген нүкте, 
-тұрақты шама.
Егер 
десек, онда 
, 
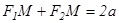. Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:
(6.3)
мұндағы 
эллипстің үлкен жарты өсі, 
оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан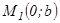 
нүктесін аламыз. 
болғандықтан 
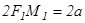немесе 
болады. Пифагор теоремасы бойынша 
. Осыдан 
деп белгілейміз. 
қатынасын эллипстің эксцентриситеті деп атайды. 
болғандықтан 
. 
эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.
Гипербола
\ Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасының абсолюттік шамасы тұрақты 2а -ға тең болатын жазықтықтағы нүктелердің геометриялық орындарын гипербола деп атайды.
Гиперболаның канондық теңдеуі былай жазылады:
(6.4)
Мұндағы 
, 
- гиперболаның нақты жарты өсі, жорымал жарты өсі, гиперболаның эксцентриситеті,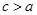 
болғандықтан 
. Егер гиперболаның 
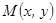нүктесі шексіздікке ұмтылғанда 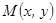нүктесінен түзуге дейінгі қашықтық нөлге ұмтылса, онда мұндай түзуді гиперболаның асиптотасы дейді. Гиперболаның асимптоталарының теңдеулері: 
және 
, мұндағы және гиперболаның жарты өстері. гиперболаның директрисаларының теңдеуі. Гиперболаның директрисалары оның төбелерінің арасында жатады.
Парабола
Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтағы нүктелердің геометриялық орындарын парабола дейді.
(6.5)
мұндағы 
берілген фокус пен директрисаның арасындағы қашықтық. Параболаның директрисасының теңдеуі: 
. параболасы 
өсіне симметриялы орналасады.
