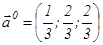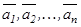векторлар жүйесі берілсін.
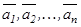векторлар жүйесі үшін бәрі бірдей нөлге тең емес және
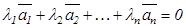
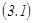
теңдігін қанағаттандыратын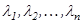 
сандары табылса, онда 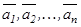векторларын сызықтық тәуелді векторлар деп атайды. Ал егер 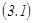теңдік тек 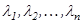сандарының барлығы бірдей нөлге тең болғанда ғана орындалса, онда 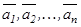векторлар жүйесі сызықтық тәуелсіз деп аталады.
Егер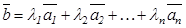 
теңдігі орындалатын 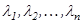сандары табылса, онда 
векторы вектор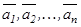ларының сызықтық комбинациясы деп аталады.
Теорема. Екі вектор сызықтық тәуелді болуы үшін олардың өзара коллинеар болуы қажетті және жеткілікті.
Бұл теоремадан кез келген коллинеар емес екі вектор сызықтық тәуелсіз болады деген қорытынды шығады.
Теорема. Үш вектор сызықтық тәуелді болуы үшін олардың компланар болуы қажетті және жеткілікті. Бұл теоремадан кез келген компланар емес үш вектор сызықтық тәуелсіз векторлар жүйесін құрайды деген қорытынды шығады. Егер жазықтықта кез келген 
векторы үшін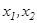 
нақты сандары табылып, мына теңдік 
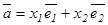орындалса, онда белгілі ретпен алынған 
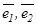сызықтық тәуелсіз векторлар жұбы жазықтықтағы базис деп аталады. Мұндағы 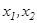сандары векторының 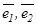базисіндегі координаттары деп аталады да былай белгіленеді: 
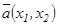. Егер кеңістікте кез келген 
векторы үшін 
нақты сандары табылып, мына теңдік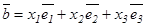 
орындалса, онда белгілі ретпен алынған сызықтық тәуелсіз 
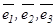векторлар үштігін кеңістіктегі базис деп атайды. Мұндағы сандары векторының 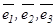базисіндегі координаттары деп аталады да былай белгіленеді: 
.
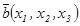Базисті құраушы векторлар базистік векторлар деп аталады. Осы анықтамалар мен теоремалардан кез келген коллинеар емес екі вектор жазықтықта, ал кез келген компланар емес үш вектор кеңістікте базистік векторлар жүйесі болады деген қорытынды шығады.
Векторды координат өстердің орттары арқылы жіктеу. Вектордың модулі. Кеңістіктегі тік бұрышты декарттық 
координаталар жүйесін қарастырайық. Ох, Оу, Oz координат өстерінің бойында жатқан бірлік (орт) векторларды сәйкесінше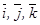 
деп белгілейік. Сонда реттелген үштік 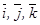кеңістікте базистік векторлар жүйесін құрайды. Мұндай, базистік векторлар жүйесін ортогональ базистік жүйе (базис) деп атайды 
. 
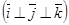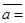
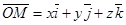, себебі үш вектордың қосындысы.
Бұл формула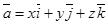 
вектордың координат өстерінің орттары арқылы жіктелген түрі деп аталады немесе қысқаша 
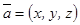деп жазады.
Екінші жағынан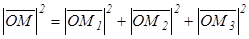 
= 
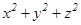, Осыдан 
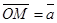болғандықтан 
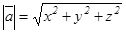- вектордың модулі (ұзындығы).
1-мысал. Егер 
, онда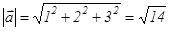 
Егер векторы Ох, Оу, Oz өстерімен сәйкесінше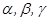 
бұрыштарын құрса, онда
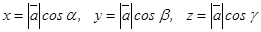, осыдан 
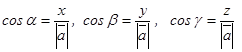болады.
Мұндағы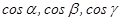 
сандары векторының бағыттаушы косинустары деп аталады. Алдыңғы өрнекті вектордың модулінің формуласына қойып,
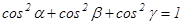теңдігін аламыз. 
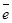бірлік векторының коодинаттары 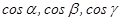екенін оңай байқауға болады. Сонымен, 
.
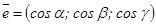2-мысал.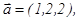 
векторы үшін 
