Взаимное положение прямых. Параллельные, пересекающиеся и скрещивающиеся прямые. Конкурирующие точки скрещивающихся прямых.

Как известно, прямые в пространстве могут быть пересекающимися, параллельными или скрещивающимися. Рассмотрим эти случаи.

Пересекающиеся прямые. Наглядное изображение двух прямых AB и CD, пересе-кающихся в точке К,приведено на рисунке 2.10, их чертеж в системе V, Н – на рисунке 2.11.

Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.

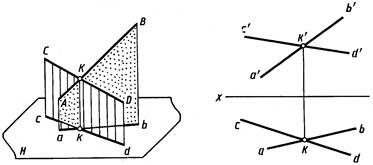
Рис.2.10 Рис.2.11

Для прямых, кроме профильных, в системе V, H справедливо и обратное утверждение:

если в системе V, H точки пересечения одноименных проекций прямых, кроме профильных, лежат на одной линии связи, то прямые пересекаются.

Если в системе V, H одна из рассматриваемых прямых профильная, то, чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.

Примеры чертежей пересекающихся и непересекающихся (скрещивающихся) прямых, из которых одна с проекциями а'b', ab, a"b"– профильная, показаны на рисунках 2.12 и 2.13.

На рисунке 2.12 все три проекции k', k, k" точки K прямой CD принадлежат и трем одноименным проекциям a'b', ab и a"b" прямой AB, т. е. прямые пересекаются.

На рисунке 2.13 профильная проекция l " точки L прямой CD не принадлежит профильной проекции a"b", следовательно, прямые AB и CD не пересекаются.

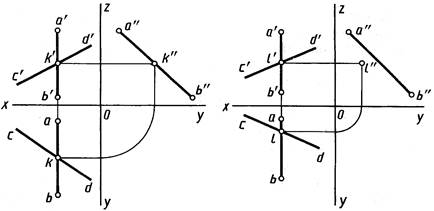
Рис.2.12 Рис.2.13

На рисунке 2.14 показаны прямые, две проекции которых пересекаются в одной точке, а две другие проекции сливаются в одну линию. Это означает, что обе прямые принадлежат плоскости P,перпендикулярной плоскости H (рис. 2.15).

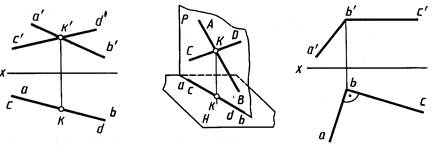
Рис. 2.14 Рис. 2.15 Рис. 2.16

Чертеж прямого угла ABC со стороной ВС,параллельной плоскости H,приведен на рисунке 2.16. Горизонтальная проекция ba стороны BA перпендикулярна горизонтальной проекции bc стороны ВС.

Эта особенность проецирования прямого угла упрощает решение ряда задач. Например, пусть требуется начертить перпендикуляр из точки с проекциями a', а к прямой с проекциями b'c', bc, параллельной плоскости V (рис. 2.17). Для этого из точки а' проводим перпендикуляр a'm' к b'c'. Построив проекцию m, проводим горизонтальную проекцию am перпендикуляра.

Это свойство будет широко использовано в дальнейшем.

Заметим, что проекция любого угла в зависимости от положения его плоскости может представлять собой острый, прямой или тупой угол (или прямую линию, если плоскость угла перпендикулярна плоскости проекций). Если угол не прямой и одна сторона его параллельна плоскости проекций, то на эту плоскость острый угол проецируется также в виде острого угла меньшей величины, тупой угол – в виде тупого угла большей величины.

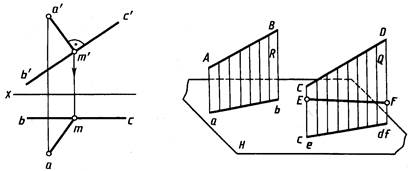
Рис. 2.17 Рис. 2.18

Параллельные прямые. Если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой. Действительно (рис.2.18), проецирующие плоскости P и Q, проведенные через параллельные прямые AB и CD, параллельны между собой. С плоскостью проекций Н онипересекаются по параллельным прямым ab и cd – проекциям прямых AB и CD на плоскости H. Однако из параллельности проекций не всегда следует параллельность прямых.

В примере на рисунке 2.19 проекции a'b', e'f', ab, еf профильных прямых AB и EF между собой параллельны. Однако из взаимного положения их профильных проекций видно, что сами прямые не параллельны.

Для прямых общего положения эти условия параллельности следующие:

если одноименные проекции прямых общего положения параллельны в системе двух плоскостей проекций, то прямые параллельны (рис. 2.20).

Для прямых частного положения:

если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые.

По рисунку 2.21 заключаем, что профильные прямые 5-6 и 7-8 параллельны, так как параллельны их профильные проекции 5"6" и 7"8".

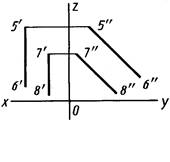
Рис. 2.19 Рис. 2.20 Рис.2.21

Скрещивающиеся прямые. Скрещивающиеся прямые не имеют общих точек. Наглядное изображение двух скрещивающихся прямых AB и CD общего положения дано на рисунке 2.22, их чертеж – на рисунке 2.23. С точкой пересечения одноименных проекций ab и cd (рис.2.22) совпадают проекции к и l двух точек К и L,принадлежащих различным прямым CD и AB.

Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи (рис. 2.23).

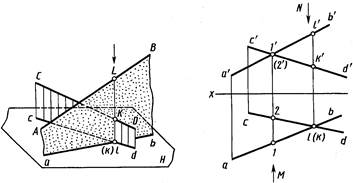
Рис.2.22 Рис.2.23

Интересен вопрос: какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю? Это определяют путем анализа положения определенных точек этих прямых.

На рисунке 2.22 видно, что при взгляде сверху по указанной стрелке точка L на прямой AB закрывает точку К (проекция точки К на плоскости H показана поэтому в скобках). Соответственно и на чертеже, приведенном на рисунке 2.23, видно, что фронтальная проекция l ' выше фронтальной проекции k', и при взгляде сверху по стрелке N при проецировании на плоскость H точка L закрывает точку K (горизонтальная проекция k показана в скобках). На плоскости V совпадают фронтальные проекции 1' и 2' точек прямых AB и CD. При взгляде спереди по стрелке M видно, что точка 1 прямой AB находится ближе к наблюдателю, и при проецировании на плоскость V точка 1 прямой AB закрывает точку 2 прямой CD (фронтальная проекция 2' точки 2показана в скобках).

Рассмотренные точки скрещивающихся прямых, проекции которых на одной из плоскостей совпадают, называют конкурирующими точками.