Ќе все конфликтные ситуации можно представить как игры с нулевой суммой, потому что интересы участников таких конфликтов не всегда противоположны. ќбобщением игр с нулевой суммой на случай не противоположных интересов участников €вл€ютс€ игры с ненулевой суммой.
–ассмотрим конечную игру с ненулевой суммой, т. е. такую, в которой множества стратегий игроков конечны: будем считать, что первый игрок может выбрать одну из m своих стратегий, обозначенных номерами 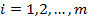 , а второй игрок Ц одну из n своих стратегий, обозначенных номерами
, а второй игрок Ц одну из n своих стратегий, обозначенных номерами  . ≈сли первый игрок выбрал свою i -ю стратегию, а второй игрок Ц свою
. ≈сли первый игрок выбрал свою i -ю стратегию, а второй игрок Ц свою  -ю стратегию, то в результате такого совместного выбора первый игрок получает выигрыш
-ю стратегию, то в результате такого совместного выбора первый игрок получает выигрыш 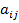 , а второй игрок Ц выигрыш
, а второй игрок Ц выигрыш 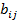 . ѕри этом не об€зательно, чтобы
. ѕри этом не об€зательно, чтобы 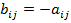 , как в матричных играх.
, как в матричных играх.
“аким образом, конечна€ игра с ненулевой суммой полностью определ€етс€ двум€ матрицами
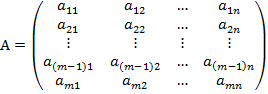 и
и 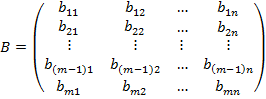 ,
,
поэтому называетс€ биматричной.
ƒопустим, матрицы игры выгл€д€т следующим образом:


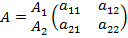 и
и 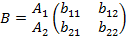 .
.
ѕрипишем стратеги€м 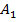 ,
, 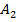 (
(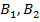 ) веро€тности
) веро€тности  ,
,  (
(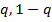 ) соответственно.
) соответственно.
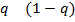
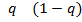
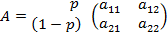 и
и 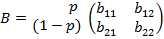 .
.
“огда средний выигрыш игрока 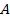 (первого игрока) равен:
(первого игрока) равен:
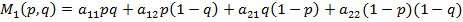 .
.
—редний выигрыш игрока  (второго игрока) равен:
(второго игрока) равен:
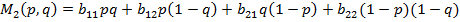 .
.
Ѕиматрична€ игра, как и матрична€, происходит парти€ми.
÷ель каждого игрока Ц выиграть как можно большую сумму в результате большого числа партий. ѕон€ти€ чистых и смешанных стратегий игроков в биматричных играх ввод€тс€ аналогично тому, как это было сделано в матричных играх.
≈сли матричные игры €вл€ютс€ играми со строгим соперничеством, поскольку выигрыш одного игрока в точности равен проигрышу другого, то в биматричных играх интересы игроков могут быть в большей или меньшей степени близки.
¬ зависимости от того, запрещено или разрешено сотрудничество игроков, различают некооперативные и кооперативные игры.
јнализ биматричной игры в некооперативном варианте сводитс€ к поиску максиминных стратегий игроков, т. е. стратегий, которые обеспечивают игрокам получение максимально возможного гарантированного выигрыша вне зависимости от действий противника.
ћножество всевозможных пар смешанных стратегий игроков обозначим
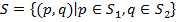 , где
, где
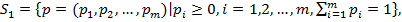
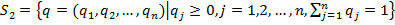 .
.
≈сли два игрока выбрали смешанные стратегии  и
и 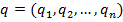 соответственно, то математические ожидани€ выигрышей игроков равны
соответственно, то математические ожидани€ выигрышей игроков равны
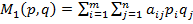
и
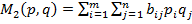 .
.
¬ажным в теории игр €вл€етс€ пон€тие равновеси€.
√овор€т, что стратегии игроков  и
и 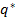 образуют равновесие Ќэша, если никому из игроков не выгодно от них отклон€тьс€ при условии, что другой игрок не следует своей равновесной стратегии, т. е. если дл€ любых стратегий
образуют равновесие Ќэша, если никому из игроков не выгодно от них отклон€тьс€ при условии, что другой игрок не следует своей равновесной стратегии, т. е. если дл€ любых стратегий 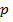 и
и  .
.
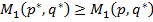 ,
,
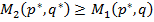 .
.
“еорема существовани€ равновесий. ¬ любой биматричной игре существует хот€ бы одно равновесие Ќэша.
Ќайти равновесные ситуации можно следующим образом.
ѕо матрице 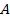 находим числа
находим числа 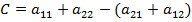 ,
, 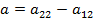 и решаем систему:
и решаем систему:
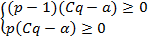 .
.
ѕо матрице  находим числа
находим числа 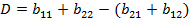 ,
, 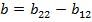 и решаем систему:
и решаем систему:
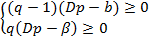 .
.
»зобразив обе полученные кривые в координатах 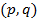 , найдем точки пересечени€ этих кривых, лежащие в квадрате
, найдем точки пересечени€ этих кривых, лежащие в квадрате 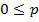 ,
, 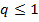 , которые определ€ют равновесные ситуации. ƒл€ каждой равновесной ситуации наход€т средние выигрыши
, которые определ€ют равновесные ситуации. ƒл€ каждой равновесной ситуации наход€т средние выигрыши 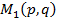 и
и 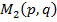 .
.
|
|
|
ритерий равновеси€. —тратегии игроков  и
и 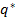 образуют равновесие Ќэша тогда и только тогда, когда при условии использовани€ первым игроком стратегии
образуют равновесие Ќэша тогда и только тогда, когда при условии использовани€ первым игроком стратегии  люба€ чиста€ стратеги€ второго игрока, соответствующа€
люба€ чиста€ стратеги€ второго игрока, соответствующа€ 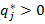 , приносит второму игроку один и тот же выигрыш
, приносит второму игроку один и тот же выигрыш  , а люба€ чиста€ стратеги€ второго игрока, соответствующа€
, а люба€ чиста€ стратеги€ второго игрока, соответствующа€ 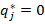 , приносит второму игроку выигрыш, не больший
, приносит второму игроку выигрыш, не больший  , а при условии использовани€ вторым игроком стратегии
, а при условии использовани€ вторым игроком стратегии 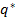 люба€ чиста€ стратеги€ первого игрока, соответствующа€
люба€ чиста€ стратеги€ первого игрока, соответствующа€ 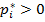 , приносит первому игроку один и тот же выигрыш
, приносит первому игроку один и тот же выигрыш  , а люба€ чиста€ стратеги€ первого игрока, соответствующа€
, а люба€ чиста€ стратеги€ первого игрока, соответствующа€ 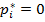 , приносит первому игроку выигрыш, не больший
, приносит первому игроку выигрыш, не больший  .
.
ƒоказательство. ѕусть пара стратегий первого и второго игрока 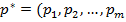 ),
), 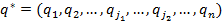 образуют равновесие Ќэша, и пусть первый игрок действует в соответствии со стратегией
образуют равновесие Ќэша, и пусть первый игрок действует в соответствии со стратегией  , не отклон€€сь от нее.
, не отклон€€сь от нее.
ѕредположим, что у второго игрока существуют такие чистые стратегии с номерами 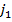 и
и 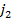 , что
, что
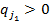
и
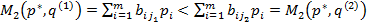 ,
,
где
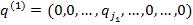
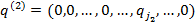 .
.
¬ этом случае второй игрок может отклонитьс€ от стратегии 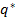 и выбрать стратегию
и выбрать стратегию 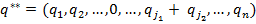 , котора€ обеспечит ему больший выигрыш, чем стратеги€
, котора€ обеспечит ему больший выигрыш, чем стратеги€ 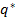 при условии, что первый игрок не будет отклон€тьс€ от стратегии
при условии, что первый игрок не будет отклон€тьс€ от стратегии  .
.
ƒействительно,
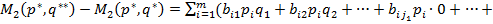
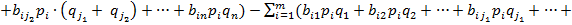
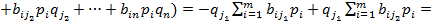
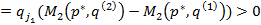
ѕолучили противоречие с предположением, что стратегии  и
и 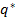 образуют равновесие Ќэша, которое доказывает теорему.
образуют равновесие Ќэша, которое доказывает теорему.
ћаксиминные смешанные стратегии первого и второго игроков обеспечивают им гарантированные выигрыши
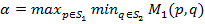 и
и 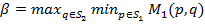
соответственно вне зависимости от поведени€ противника.
ѕо-другому максиминные стратегии называютс€ осторожными Ц смысл этого названи€ очевиден, и в некооперативном случае игрокам имеет смысл придерживатьс€ своих осторожных стратегий.
ѕример 3.1. (»гра Ђƒилемма заключенныхї). ƒвое преступников (первый и второй игроки), подозреваемые в совместном совершении т€жкого преступлени€, наход€тс€ изолированно друг от друга в предварительном заключении. ѕр€мые улики у следстви€ отсутствуют, поэтому успех обвинени€ зависит от того, признаютс€ ли заключенные. ” каждого из заключенных есть две стратегии: признатьс€ (перва€ стратеги€) или не признаватьс€ (втора€ стратеги€). ≈сли оба преступника признаютс€, то они будут признаны виновными и приговорены к восьми годам заключени€. ≈сли ни один из них не признаетс€, то по обвинению в основном преступлении они будут оправданы, но суд все-таки признает их вину в менее значительном преступлении (например, в ношении оружи€), в результате чего оба будут приговорены к одному году заключени€. ≈сли же признаетс€ только один и них, то признавшийс€ будет освобожден (за помощь следствию), а другой преступник будет приговорен к максимальному сроку заключени€ Ц к дес€ти годам. “ребуетс€ определить максиминные стратегии игроков и равновеси€ Ќэша, если такие есть.
–ешение 1. ћатрицы выигрышей игроков таковы:
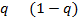
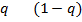
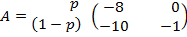 и
и 
—мешанные стратегии игроков представим в виде 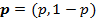 и
и 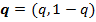 , где
, где 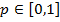 ,
, 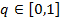 .
.
ѕри этом математическое ожидание выигрыша первого игрока равно
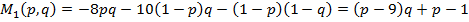 .
.
јналогично определ€етс€ математическое ожидание выигрыша второго игрока:
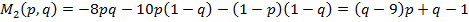 .
.
Ќаилучший гарантированный выигрыш первого игрока равен
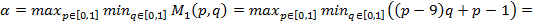
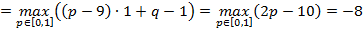
”чли, что 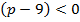 , так как
, так как 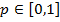 , поэтому вне зависимости от
, поэтому вне зависимости от 
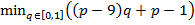 будет достигатьс€ при
будет достигатьс€ при 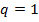 , а максиминна€ стратеги€ первого игрока, соответствующа€ этому наилучшему гарантированному выигрышу,
, а максиминна€ стратеги€ первого игрока, соответствующа€ этому наилучшему гарантированному выигрышу, 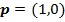 , т. е. максиминна€ стратеги€ первого игрока Ц признатьс€ и получить восемь лет заключени€.
, т. е. максиминна€ стратеги€ первого игрока Ц признатьс€ и получить восемь лет заключени€.
|
|
|
јналогично находим наилучший гарантированный выигрыш второго игрока
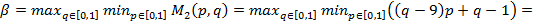
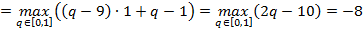
и его максиминную стратегию 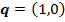 Ц признатьс€.
Ц признатьс€.
ќчевидно, максиминные стратегии образуют равновесие Ќэша.
–ешение 2. ѕо матрице 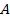 находим числа
находим числа 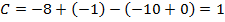 ,
, 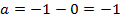 и решаем систему:
и решаем систему:
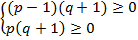 .
.
где получим 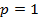 .
.
ѕо матрице  находим числа
находим числа 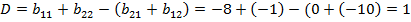 ,
,  и решаем систему:
и решаем систему:
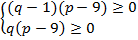 .
.
где получим 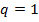 .
.
“огда средний выигрыш игрока 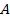 (первого игрока) равен:
(первого игрока) равен:
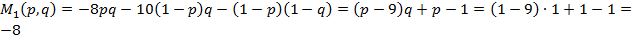 .
.
—редний выигрыш игрока  (второго игрока) равен:
(второго игрока) равен:
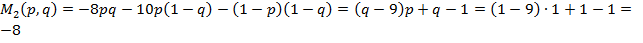 .
.
ќчевидно, максиминные стратегии образуют равновесие Ќэша.
ѕример 3.2 (»гра Ђсемейный спорї). ƒва игрока (муж и жена) выбирают, где провести вечер. ” каждого из них есть две стратегии: выбрать посещение футбольного матча (перва€ стратеги€) или оперного спектакл€ (втора€ стратеги€). ѕолезность совместного похода в театр муж оценивает в одну единицу, а жена в две, полезность совместного похода на футбол, наоборот, жена оценивает в одну единицу, а муж в две. ≈сли же супруги идут в разные места, вечер оказываетс€ испорченным, что соответствует нулевым полезност€м дл€ обоих игроков. “ребуетс€ определить макси-минные стратегии игроков и равновеси€ Ќэша, если такие есть.
–ешение. —оставим матрицы выигрышей игроков:
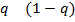
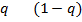
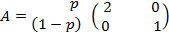 и
и 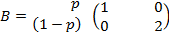
—мешанные стратегии игроков представим в виде 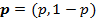 и
и 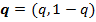 , где
, где 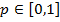 ,
, 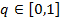 .
.
ѕри этом математические ожидани€ выигрышей игроков равны
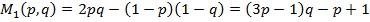 .
.
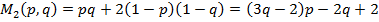 .
.
Ќаилучшие гарантированные выигрыши игроков
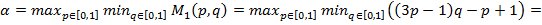
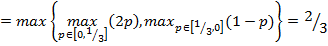 ;
;
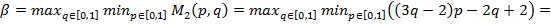
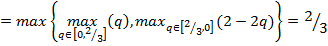 ,
,
а соответствующие максиминные стратегии таковы: 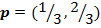 и
и 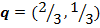 .
.
»ным способом:
ѕо матрице 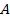 находим числа
находим числа 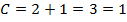 ,
, 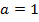 и решаем систему:
и решаем систему:
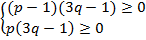 .
.
где получим 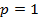 ;
; 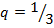 .
.
ѕо матрице  находим числа
находим числа 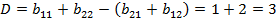 ,
, 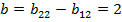 и решаем систему:
и решаем систему:
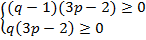 .
.
где получим 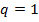 ;
; 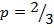
“огда средний выигрыш игрока 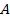 (первого игрока) равен:
(первого игрока) равен:
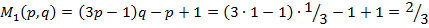 .
.
—редний выигрыш игрока  (второго игрока) равен:
(второго игрока) равен:
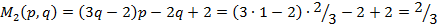 .
.
Ёто означает, что муж должен в 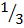 вечеров выбирать футбол и в
вечеров выбирать футбол и в 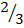 вечеров театр, а жена должна в
вечеров театр, а жена должна в 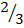 вечеров выбирать футбол и в
вечеров выбирать футбол и в 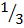 вечеров театр, тогда в среднем и муж, и жена будут выигрывать по
вечеров театр, тогда в среднем и муж, и жена будут выигрывать по 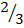 за одну партию.
за одну партию.
–авновесий Ќэша в данной игре целых три:
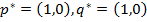 ;
;
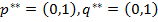 ;
;
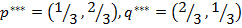 .
.
¬ отличие от матричных игр, в биматричных играх может оказатьс€ так, что совместное отклонение двум€ игроками от равновесий Ќэша (или от максиминных стратегий) приводит к увеличению выигрыша обоих игроков. Ёто иллюстрируетс€ следующими примерами.
≈сли в примере 3.1 один из игроков будет придерживатьс€ максиминной стратегии и признаетс€, а другой игрок отклонитс€ от своей максиминной стратегии и признаватьс€ не будет, то тот, кто не признаетс€, получит дес€ть лет заключени€ вместо восьми (в результате его положение ухудшитс€, а положение его соучастника улучшитс€).
—ущественным отличием биматричных игр от матричных €вл€ютс€ то, что возможны ситуации, когда отклонение обоих игроков от максиминных стратегий приводит к увеличению их выигрышей: если в примере 3.1 оба преступника не признаютс€, то оба получат всего по одному году. Ёто и €вл€етс€ основой дилеммы, котора€ стоит перед каждым из заключенных: поскольку переговоры друг с другом невозможны, каждый из двух заключенных делает выбор, признаватьс€ или нет, не зна€, созналс€ ли его соучастник.
¬ примере 3.2 ситуаци€ еще сложнее: участники могут увеличить свои выигрыши, совместно отклонившись от максиминных стратегий, в нескольких ситуаци€х. Ќапример, если вместо максиминных стратегий 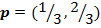 и
и 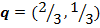 игроки выберут соответственно стратегии
игроки выберут соответственно стратегии 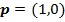 и
и 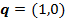 , то их выигрыши состав€т 2 дл€ мужа и 1 дл€ жены (оба эти выигрыша больше
, то их выигрыши состав€т 2 дл€ мужа и 1 дл€ жены (оба эти выигрыша больше 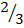 ). Ќо есть и друга€ ситуаци€: если вместо максиминных стратегий игроки выберут стратегии
). Ќо есть и друга€ ситуаци€: если вместо максиминных стратегий игроки выберут стратегии 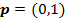 и
и 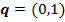 , то их выигрыши состав€т 1 дл€ мужа и 2 дл€ жены (что оп€ть превышает максиминные выигрыши). ≈сли переговоры между участниками невозможны, отклон€тьс€ от максиминных стратегий опасно, так как даже если есть возможность выиграть больше, эта возможность сопр€жена с риском уменьшени€ выигрыша. Ќапример, если муж выберет театр Ц
, то их выигрыши состав€т 1 дл€ мужа и 2 дл€ жены (что оп€ть превышает максиминные выигрыши). ≈сли переговоры между участниками невозможны, отклон€тьс€ от максиминных стратегий опасно, так как даже если есть возможность выиграть больше, эта возможность сопр€жена с риском уменьшени€ выигрыша. Ќапример, если муж выберет театр Ц 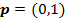 , а жена футбол Ц
, а жена футбол Ц 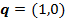 , или наоборот, то выигрыши обоих игроков будут равны нулю.
, или наоборот, то выигрыши обоих игроков будут равны нулю.
¬ыходом в таких ситуаци€х €вл€етс€ коопераци€ игроков, т. е. сотрудничество, состо€щее в том, что игроки могут договоритьс€ о совместном выборе стратегий.
|
|
|
ѕерейдем к обсуждению возможностей кооперативного поведени€ игроков.
–анее предполагалось, что в процессе игры отсутствует €вный обмен информацией между участниками. аждый игрок определ€л свою линию поведени€, исход€ из своей функции выигрыша, и, безусловно, основыва€сь на том, что другие игроки действуют аналогично. ѕри этом считалось, что игроки знают функции выигрыша друг друга, но в непосредственный контакт не вступают.
ћежду тем в реальных экономических ситуаци€х участники конфликтов активно взаимодействуют друг с другом: вступают в переговоры, заключают соглашени€, создают коалиции, примен€ют угрозы и подкупы и т. д. ¬се эти процессы могут в различной степени получать отражени€ в игровых модел€х.
»гры, в которых возможны непосредственные контакты между участниками, называютс€ кооперативными. ≈сли игроки могут вступать в переговоры и образовывать коалиции, то какие исходы могут стать результатом переговоров.
–ассмотрим биматричную игру, в которой выигрыши первого и второго игроков заданы матрицами 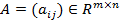 и
и 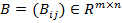 .
.
ѕусть  и
и  Ц смешанные стратегии игроков. “ак как
Ц смешанные стратегии игроков. “ак как 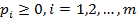 ,
,  ,
, 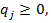
 ,
,  , множество всех возможных вариантов пар выигрышей
, множество всех возможных вариантов пар выигрышей
(
представл€ет собой выпуклую оболочку точек плоскости с координатами (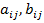 ),
), 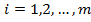 и
и  ; эти точки (
; эти точки (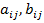 ) соответствуют парам выигрышей игроков в случае выбора ими своих чистых стратегий.
) соответствуют парам выигрышей игроков в случае выбора ими своих чистых стратегий.
ѕри этом точка (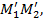 ) доминирует точку (
) доминирует точку ( ), если
), если
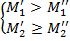 или
или 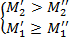
это означает, что при переходе от первой точки ко второй выигрыш каждого из игроков не уменьшитс€, и при этом хот€ бы у одного из игроков выигрыш увеличитс€.
ћножество точек, оптимальных по ѕарето (т. е. не доминируемых другими), описываетс€ так:
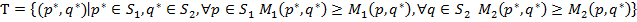 .
.
≈сли выбрать из множества точек, оптимальных по ѕарето, те точки, в которых выигрыши первого и второго игроков окажутс€ не меньше их максиминных выигрышей α и β, то получитс€ переговорное множество
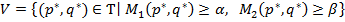 .
.
»грокам, естественно, имеет смысл выбирать свои оптимальные стратегии, соответствующие точкам из переговорного множества.
—уществуют различные способы достижени€ игроками договоренности о совместном выборе точки из переговорного множества. —амый простой из них заключаетс€ в выборе таких чистых стратегий, которые принос€т игрокам наибольший суммарный доход, из которого один из игроков платит другому оговоренную сумму. Ётот способ, конечно же, предполагает полностью доверительные отношени€ между игроками.
≈сли же договоритьс€ о выборе точки из переговорного множества игрокам не удаетс€, то можно предложить им применить одну из так называемых арбитражных схем. Ќапример, арбитражна€ схема Ќэша предлагает игрокам выбрать из переговорного множества решение Ќэша Ч такую пару смешанных стратегий, котора€ доставл€ет максимум функции Ќэша, котора€ равна произведению превышений выигрышей игроков над гарантированными (минимаксными) выигрышами.
–еализаци€ алгоритма Ќэша предполагает решение задачи математического программировани€
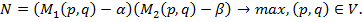
÷елева€ функци€ этой задачи называетс€ функцией Ќэша, а оптимальное решение данной Ч решением Ќэша.
–ешение этой задачи всегда существует, и если в переговорном множестве V есть хот€ бы одна точка  , така€ что
, така€ что 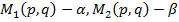 , то решение задачи единственно.
, то решение задачи единственно.
ѕример 3.3 (»гра Ђƒилемма заключенныхї в кооперативном варианте). “ребуетс€ найти переговорное множество и решение Ќэша в игре, описанной в примере 3.1 (ƒвое преступников (первый и второй игроки), подозреваемые в совместном совершении т€жкого преступлени€, наход€тс€ изолированно друг от друга в предварительном заключении. ѕр€мые улики у следстви€ отсутствуют, поэтому успех обвинени€ зависит от того, признаютс€ ли заключенные. ” каждого из заключенных есть две стратегии: признатьс€ (перва€ стратеги€) или не признаватьс€ (втора€ стратеги€). ≈сли оба преступника признаютс€, то они будут признаны виновными и приговорены к восьми годам заключени€. ≈сли ни один из них не признаетс€, то по обвинению в основном преступлении они будут оправданы, но суд все-таки признает их вину в менее значительном преступлении (например, в ношении оружи€), в результате чего оба будут приговорены к одному году заключени€. ≈сли же признаетс€ только один и них, то признавшийс€ будет освобожден (за помощь следствию), а другой преступник будет приговорен к максимальному сроку заключени€ Ц к дес€ти годам. “ребуетс€ определить максиминные стратегии игроков и равновеси€ Ќэша, если такие есть) при условии, что заключенные могут обмениватьс€ информацией.
|
|
|
–ешение. ћножество всех возможных пар выигрышей игроков представлено четырехугольником ABCD на рис. 3.1.
| — |
| F |
| D |
| ¬ |
| ≈ |
| β=-8 |
| α=-8 |
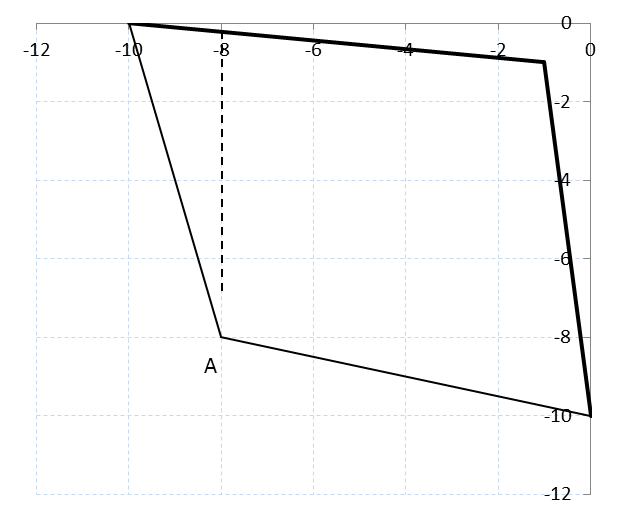
–ис. 3.1 - ћножество ожидаемых выигрышей, множество ѕарето и переговорное множество в кооперативном варианте игры Ђƒилемма заключенныхї
ќчевидно, множество ѕарето соответствует ломаной BCD, а переговорное множество Ч ломаной ECF.
ѕр€ма€, проход€ща€ через точки B(-10, 0) и C(-1, -1), задаетс€ уравнением M2 = (‑M1‑10)/9, а пр€ма€, проход€ща€ через точки C(-1, -1) и D(0, -10), Ч уравнением M2 = ‑9M1 - 10, поэтому функци€ Ќэша
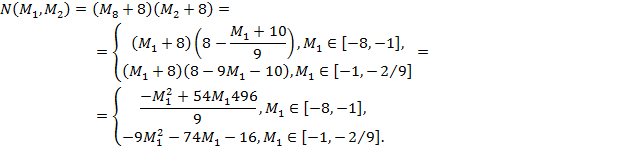
‘ункцию Ќэша мы рассматриваем на переговорном множестве, т. е. на ломаной ECF, при этом отрезок EC задаетс€ уравнением M2 = (-M1 -10)/ 9 при M1  [-8, -1], а отрезок CF задаетс€ уравнением M2 = -9M1 -10 при M2 = -9M1 -10
[-8, -1], а отрезок CF задаетс€ уравнением M2 = -9M1 -10 при M2 = -9M1 -10  [-8, -1] (или, что эквивалентно, при M1
[-8, -1] (или, что эквивалентно, при M1 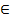 [-1, -2/9]).
[-1, -2/9]).
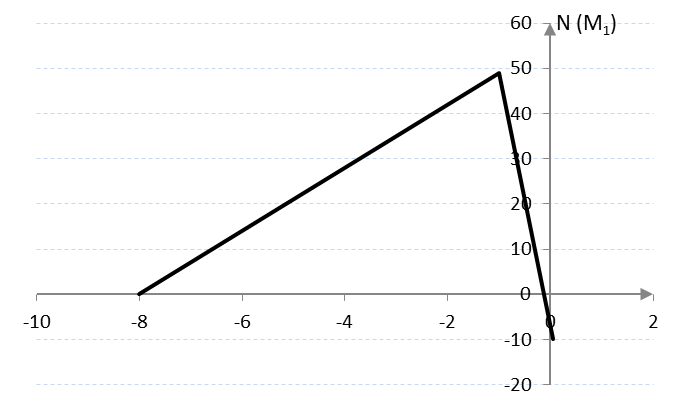
ћаксимум функции Ќэша на переговорном множестве достигаетс€ в точке 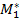 = -1 (график функции Ќэша представлен на рис. 3.2).
= -1 (график функции Ќэша представлен на рис. 3.2).
ѕри этом 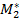 = -9
= -9 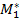 -10 = -1.
-10 = -1.
Ќа рис. 3.1 решение Ќэша соответствует точке C, поэтому если заключенные имеют возможность переговариватьс€, то они могут договоритьс€ не признаватьс€ вдвоем, и тогда получат всего по одному году заключени€.
| M1 |
–ис. 3.2 Ц √рафик функции Ќэша в кооперативном варианте игры Ђƒилемма заключенныхї
ѕример 3.4 (»гра Ђ—емейный спорї в кооперативном варианте). “ребуетс€ найти переговорное множество и решение Ќэша в игре, описанной в примере 3.2 (ƒва игрока (муж и жена) выбирают, где провести вечер. ” каждого из них есть две стратегии: выбрать посещение футбольного матча (перва€ стратеги€) или оперного спектакл€ (втора€ стратеги€). ѕолезность совместного похода в театр муж оценивает в одну единицу, а жена в две, полезность совместного похода на футбол, наоборот, жена оценивает в одну единицу, а муж в две. ≈сли же супруги идут в разные места, вечер оказываетс€ испорченным, что соответствует нулевым полезност€м дл€ обоих игроков. “ребуетс€ определить макси-минные стратегии игроков и равновеси€ Ќэша, если такие есть) при условии, что игроки могут обмениватьс€ информацией.
–ешение. ћножество всех возможных пар выигрышей игроков представлено треугольником OAB на рис. 3.3. ќчевидно, и множество ѕарето, и переговорное множество соответствуют отрезку AB.
|
|
|
ѕр€ма€, проход€ща€ через точки A (1, 2) и B (2, 1), задаетс€ уравнением M2 = 3 - M1, поэтому функци€ Ќэша
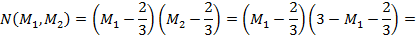
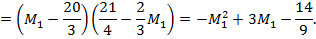
Ёта функци€ достигает максимума при 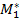 = (-3)/[2×(-1)]=1,5. ѕри этом
= (-3)/[2×(-1)]=1,5. ѕри этом 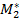 = 3 ‑
= 3 ‑ 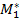 = 1,5.
= 1,5.
“очка (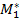 ,
, 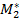 ) на рис. 3.3 обозначена D. ќна находитс€ ровно посередине отрезка AB, поэтому решение Ќэша таково:
) на рис. 3.3 обозначена D. ќна находитс€ ровно посередине отрезка AB, поэтому решение Ќэша таково:  = (1/2,1/2) и
= (1/2,1/2) и 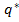 = (1/2,1/2).
= (1/2,1/2).
Ёто означает, что игроки могут договоритьс€ выбирать (случайным образом и независимо друг от друга) в половине случаев театр, и в другой половине Ч футбол, тогда выигрыш каждого составит в среднем 1,5 единицы за один вечер.
| M2 |
| α=2/3 |
| β=2/3 |
| D |
| B |
| A |
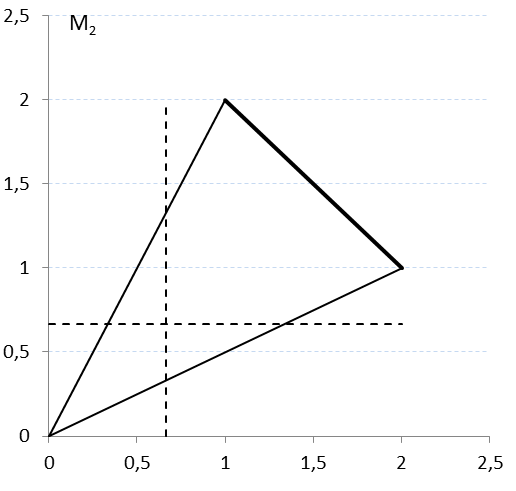
–ис 3.3 Ц ћножество ожидаемых выигрышей, множество ѕарето и переговорное множество в кооперативном варианте игры Ђ—емейный спорї
ѕример 3.5. “ребуетс€ провести анализ биматричной игры, заданной матрицами
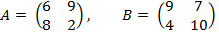
–ешение. ѕусть р = (р,1 - р) и q = (q,1 - q), где р 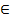 [0,1], q
[0,1], q 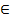 [0,1], - смешанные стратегии игроков. “огда математические ожидани€ выигрышей игроков равны соответственно
[0,1], - смешанные стратегии игроков. “огда математические ожидани€ выигрышей игроков равны соответственно
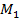 (р,q) = 6pq + 9р(1 - q) + 8(1 - p)q + 2(1 - р)(1 - q) = (6-9p)q + 7р + 2,
(р,q) = 6pq + 9р(1 - q) + 8(1 - p)q + 2(1 - р)(1 - q) = (6-9p)q + 7р + 2,
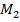 (р,q) = 9pq + 7р(1 - q) + 4(1 - p)q +10(1 - р)(1 - q) = (8q - 3)р - 6q +10.
(р,q) = 9pq + 7р(1 - q) + 4(1 - p)q +10(1 - р)(1 - q) = (8q - 3)р - 6q +10.
ћаксиминные стратегии игроков определ€ютс€ из условий
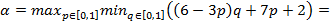
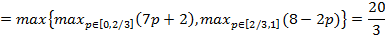
(где максимум достигаетс€ при  = 2/3),
= 2/3),
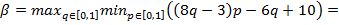
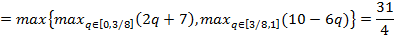
(где максимум достигаетс€ при 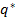 = 3/8).
= 3/8).
“аким образом, максиминные стратегии первого и второго игрока равны р = (2/3,1/3) и q = (3/8,5/8), а их гарантированные выигрыши составл€ют 20/3 и 31/4 соответственно.
ћножество всех возможных пар выигрышей игроков представлено четырехугольником ABCD на рис. 3.4. ќчевидно, множество ѕарето соответствует отрезку BC, а переговорное множество Ч отрезку EF.
ѕр€ма€, проход€ща€ через точки B(6, 9) и C(9, 7), задаетс€ уравнением M2 = 13 ‑ 2M1/3, поэтому функци€ Ќэша
N (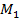 ,
, 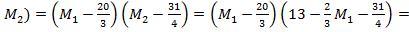
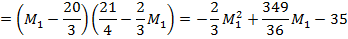
на отрезке M1  [20/3,63/8] (т. е. на отрезке EF; при M2 = 31/4 значение M1 = 3(13 ‑ 31 / 4) / 2 = 63/8) достигает максимума в точке
[20/3,63/8] (т. е. на отрезке EF; при M2 = 31/4 значение M1 = 3(13 ‑ 31 / 4) / 2 = 63/8) достигает максимума в точке 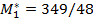 . ѕри этом
. ѕри этом
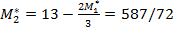 . Ёта точка на рис. 3.4 обозначена G.
. Ёта точка на рис. 3.4 обозначена G.
“очка G( 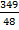 ,
, 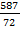 ) €вл€етс€ выпуклой комбинацией точек B (6, 9) и C (9, 7), т. е.
) €вл€етс€ выпуклой комбинацией точек B (6, 9) и C (9, 7), т. е.
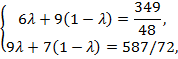
откуда λ = 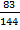 .
.
“очка ¬ соответствует выбору обоими игроками своих первых чистых стратегий, точка C соответствует выбору первым игроком своей первой чистой стратегии, а вторым игроком Ч своей второй чистой стратегии, поэтому точка G соответствует тому, что первый игрок выбирает свою первую чистую стратегию, а второй игрок с веро€тностью
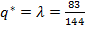 выбирает первую чистую стратегию, и с веро€тностью
выбирает первую чистую стратегию, и с веро€тностью
1 - 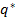 =
= 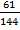 Ч вторую чистую стратегию.
Ч вторую чистую стратегию.
“аким образом, решение Ќэша таково:  =(1,0),
=(1,0), 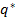 =(83/144,61/144). ѕри этом средний выигрыш первого игрока равен
=(83/144,61/144). ѕри этом средний выигрыш первого игрока равен 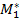 = 349/48, а средний выигрыш второго игрока Ч
= 349/48, а средний выигрыш второго игрока Ч 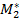 = 587/72.
= 587/72.
| α=20/3 |
| β=31/4 |
| M1 |
| M2 |
| F |
| G |
| E |
| C |
| D |
| ¬ |
–ис. 3.4 Ц ћножество ожидаемых выигрышей, множество ѕарето и переговорное множество в примере 3.5
Ќепрерывные игры
»гра с нулевой или ненулевой суммой называетс€ непрерывной, если множества стратегий участников игры целиком заполн€ют некоторые отрезки.
—мешанные стратегии в непрерывных играх задаютс€ уже не наборами веро€тностей, а функци€ми (или плотност€ми) распределени€ непрерывных случайных величин на соответствующих отрезках. ѕри этом математические ожидани€ выигрышей из сумм превращаютс€ в интегралы.
ћожно доказать, что если в непрерывной игре с нулевой суммой функци€ выигрыша первого игрока непрерывна по всем переменным, то у игроков есть оптимальные смешанные стратегии.
–ассмотрим пример непрерывной игры с нулевой суммой.
ѕример 4.1 (»гра ЂЎумна€ дуэльї). ¬ дуэли принимают участие двое. ¬ начальный момент дуэл€нты наход€тс€ на рассто€нии d0 и по команде начинают сближатьс€. ¬ распор€жении каждого дуэл€нта имеетс€ один выстрел, который он может произвести в противника с любого рассто€ни€ (конечно при условии, что дуэл€нт жив), он может даже подойти к противнику вплотную. ѕусть функции pk(d) задают веро€тности поражени€ противника k -м игроком (k = 1, 2) с рассто€ни€ d. ѕредположим, что эти функции непрерывны и убывают на отрезке [0, d 0]. –ассматриваетс€ шумна€ дуэль, когда противники слышат выстрелы друг друга. “ребуетс€ формализовать поведение игроков в виде непрерывной игры с нулевой суммой и определить оптимальные чистые стратегии игроков (если такие стратегии существуют).
–ешение. —тратегии первого и второго игроков определ€ютс€ выбором чисел
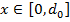 ,
, 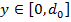 Ч рассто€ний, с которых дуэл€нты намечают произвести свои выстрелы.
Ч рассто€ний, с которых дуэл€нты намечают произвести свои выстрелы.
¬ыигрышем F(x, y) первого дуэл€нта, если он стрел€ет с рассто€ни€ x, а его противник Ч с рассто€ни€ y, удобно считать веро€тность того, что первый дуэл€нт поразит второго. ќчевидно,

(«десь мы учли, что если x < у, и второй игрок промахнетс€, то первый, услышав выстрел противника, стрел€ет в него с рассто€ни€ 0 вместо x.)
ѕокажем, что шумна€ дуэль имеет решение в чистых стратеги€х: эти стратегии таковы: 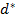 дл€ первого дуэл€нта,
дл€ первого дуэл€нта, 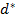 дл€ второго, при этом цена игры равна
дл€ второго, при этом цена игры равна 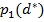 [здесь
[здесь 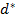 Ч единственный корень уравнени€
Ч единственный корень уравнени€ 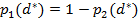 ]. ƒействительно,
]. ƒействительно,
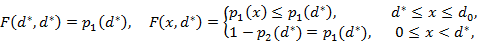
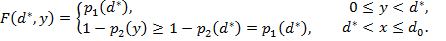
“аким образом, 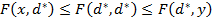 дл€ любых
дл€ любых 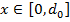 ,
, 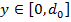 , откуда и следует, что (
, откуда и следует, что (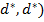 Ч седлова€ точка данной игры.
Ч седлова€ точка данной игры.
¬ частности, если меткость игроков одинакова [т. е. 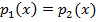 ], то цена игры, очевидно, равна 1/2, а
], то цена игры, очевидно, равна 1/2, а 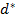 €вл€етс€ корнем уравнени€
€вл€етс€ корнем уравнени€ 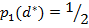 .
.
¬ бесшумной дуэли игроки не слышат выстрелов друг друга, поэтому
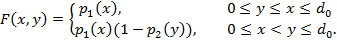
„итателю предлагаетс€ доказать, что бесшумна€ дуэль не имеет решений в чистых стратеги€х.
ѕереход€ к рассмотрению непрерывных игр с непротивоположными интересами, отметим, что решение Ќэша (и в конечных играх, и в непрерывных) имеет серьезный недостаток, который заключаетс€ в том, что оно не принимает в расчет угрозы. Ёто иллюстрирует пример игры Ђ–аботодатель Ч работникї, в которой работник имеет возможность установить интенсивность своей работы от 100% (полезность этой ситуации дл€ работника оцениваетс€ нулем, а дл€ работодател€ прибылью 1 млн. руб.) до 0% (в этом случае работник будет голодать, и полезность этой ситуации дл€ работника оцениваетс€ в ‑500 000 руб., а работодатель получит нулевую прибыль). –аботодатель может поделитьс€ с работником частью прибыли (если захочет). ћинимаксные выигрыши игроков равны нулю, а решение Ќэша (в чем мы предлагаем убедитьс€ читателю) состоит в том, что работодатель и работник дел€т прибыль поровну Ч по 500 тыс. руб. ќднако при этом игнорируетс€ тот факт, что работодатель находитс€ в гораздо более выгодном положении, чем работник. ƒействительно, работник может воспреп€тствовать работодателю, только решившись на очень трудный шаг; угроза прекратить работу с его стороны не очень правдоподобна, и в результате работник, скорее всего, будет продолжать работать за зарплату даже в том случае, если работодатель не будет делитьс€ с ним прибылью. ”гроза же работодател€ уменьшить сумму, которой он делитс€ с работником, вполне реальна.
ѕозиционные игры
¬се игры, которые рассматривались до сих пор, были заданы в так называемой нормальной форме, котора€ предполагает, что:
1) задано множество игроков I (не ограничива€ общности, можно считать, что k игроков заданы своими номерами, т. е. I = {1, 2, Е, k };
2) дл€ каждого игрока 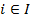 задано множество возможных стратегий
задано множество возможных стратегий 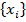 ;
;
3) дл€ каждой ситуации (т. е. совместного выбора игроками своих стратегий:  Ч первым игроком,
Ч первым игроком, 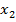 Ч вторым, Е,
Ч вторым, Е, 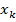 Ч k -м игроком) заданы выигрыши игроков:
Ч k -м игроком) заданы выигрыши игроков: 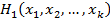 Ч первого,
Ч первого, 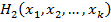 Ч второго, Е,
Ч второго, Е, 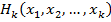 Ч k -го, т. е. заданы функции выигрышей.
Ч k -го, т. е. заданы функции выигрышей.






