≈сли матрица игры содержит несколько одинаковых строк (столбцов), то из них оставл€ют только одну строку (один столбец), а остальные строки (столбцы) отбрасываютс€. ќтброшенным стратеги€м приписываютс€ нулевые веро€тности. Ёто Ц дублирование стратегий.
≈сли i -€ строка поэлементно не меньше ( ) j -й строки, то говор€т, что i -€ строка доминирует на j -й строкой. ѕоэтому игрок
) j -й строки, то говор€т, что i -€ строка доминирует на j -й строкой. ѕоэтому игрок 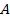 не использует j -ю стратегию, так как его выигрыш при i -й стратегии не меньше, чем при j -й стратегии. ¬не зависимости от того, как играет игрок
не использует j -ю стратегию, так как его выигрыш при i -й стратегии не меньше, чем при j -й стратегии. ¬не зависимости от того, как играет игрок  .
.
јналогично, если i -й столбец поэлементно не меньше  j -го столбца, то говор€т, что j -й столбец доминирует над i -м столбцом. ѕоэтому игрок
j -го столбца, то говор€т, что j -й столбец доминирует над i -м столбцом. ѕоэтому игрок  не использует i -ю стратегию. “ак как его проигрыш (равный выигрышу игрока
не использует i -ю стратегию. “ак как его проигрыш (равный выигрышу игрока 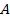 ) при j -й стратегии не больше (
) при j -й стратегии не больше ( ), чем при i -й стратегии, вне зависимости от того, как играет игрок
), чем при i -й стратегии, вне зависимости от того, как играет игрок 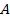 . Ёто Ц доминирование стратегий.
. Ёто Ц доминирование стратегий.
≈сли игра  имеет седловую точку, то после упрощени€ получитс€ игра 1
имеет седловую точку, то после упрощени€ получитс€ игра 1  1.
1.
ѕример 1.3. —ледует упростить матрицу игры:
 .
.
ѕерва€ и четверта€ строки равны, поэтому отбросим четвертую строку, а веро€тность будет  .
.
ѕолучим матрицу  .
.
¬тора€ строка доминирует на третьей строкой ( ). ѕоэтому отбросим третью строку, а веро€тность будет
). ѕоэтому отбросим третью строку, а веро€тность будет  .
.
ѕолучим матрицу  .
.
¬торой столбец доминирует на третьим ( . ѕоэтому отбросим третий столбец, а веро€тность будет
. ѕоэтому отбросим третий столбец, а веро€тность будет 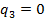 .
.
ѕолучим матрицу  .
.
—троки между собой несравнимы ( ), столбцы тоже (
), столбцы тоже ( ). ƒальнейшее упрощение невозможно. »гра сведена от
). ƒальнейшее упрощение невозможно. »гра сведена от  к игре
к игре 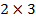 .
.
–ешение игры 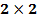
ѕример 1.4. Ќайдем решение матричной игры 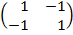
ѕрипишем строкам веро€тности  и
и 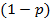 соответственно.
соответственно.
 .
.
”множив столбец  поэлементно на первый столбец и сложив произведени€, получим линейную зависимость
поэлементно на первый столбец и сложив произведени€, получим линейную зависимость  . Ёто средний выигрыш игрока
. Ёто средний выигрыш игрока 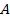 при применении игроком
при применении игроком  своей первой стратегии.
своей первой стратегии.
”множив столбец  поэлементно на второй столбец и сложив произведени€, получим линейную зависимость
поэлементно на второй столбец и сложив произведени€, получим линейную зависимость 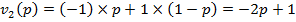 . Ёто средний выигрыш игрока
. Ёто средний выигрыш игрока 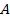 при применении игроком
при применении игроком  своей второй стратегии.
своей второй стратегии.
ѕриравн€ем полученные зависимости:  . ѕолучим
. ѕолучим  ,
,
 , т.е. оптимальна€ смешанна€ стратеги€ игрока
, т.е. оптимальна€ смешанна€ стратеги€ игрока 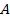
 . ѕодставив
. ѕодставив  в любую из зависимостей, получим цену игры
в любую из зависимостей, получим цену игры  .
.
ѕрипишем столбцам веро€тности  и
и  соответственно.
соответственно.


 .
.
”множив строку ( ,
,  ) на первую строку и сложив произведени€, получим линейную зависимость
) на первую строку и сложив произведени€, получим линейную зависимость  . Ёто средний выигрыш игрока
. Ёто средний выигрыш игрока 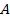 (проигрыш игрока
(проигрыш игрока  ) при применении игроком
) при применении игроком 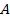 своей первой стратегии.
своей первой стратегии.
”множив строку ( ,
,  ) на вторую строку и сложив произведени€, получим линейную зависимость
) на вторую строку и сложив произведени€, получим линейную зависимость 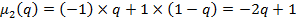 . Ёто средний выигрыш игрока
. Ёто средний выигрыш игрока 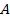 (проигрыш игрока
(проигрыш игрока  ) при применении игроком
) при применении игроком  своей второй стратегии.
своей второй стратегии.
ѕриравн€ем полученные зависимости:  . »меем
. »меем  ,
,  , т.е. оптимальна€ смешанна€ стратеги€ игрока
, т.е. оптимальна€ смешанна€ стратеги€ игрока 
 .
.
“аким образом, каждую стратегию необходимо примен€ть с частотой  .
.
ѕример 1.5. Ќайти решение игры из примера 1.2 в смешанных стратеги€х.
–ешение. ѕлатежна€ матрица, построенна€ ранее:

ѕусть первый игрок выбирает свою первую стратегию с веро€тностью  , а вторую Ц с веро€тностью
, а вторую Ц с веро€тностью 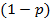 , т.е. первый игрок играет со смешанной стратегией
, т.е. первый игрок играет со смешанной стратегией  .
.
ќбозначим  ожидаемый выигрыш, т.е. математическое ожидание выигрыша, первого игрока, если второй игрок при этом выберет свою j -ю стратегию. ¬ рассматриваемом примере
ожидаемый выигрыш, т.е. математическое ожидание выигрыша, первого игрока, если второй игрок при этом выберет свою j -ю стратегию. ¬ рассматриваемом примере  ,
,  . ѕостроим графики этих функций, представленные на рисунке 1.1.
. ѕостроим графики этих функций, представленные на рисунке 1.1.
|
|
|
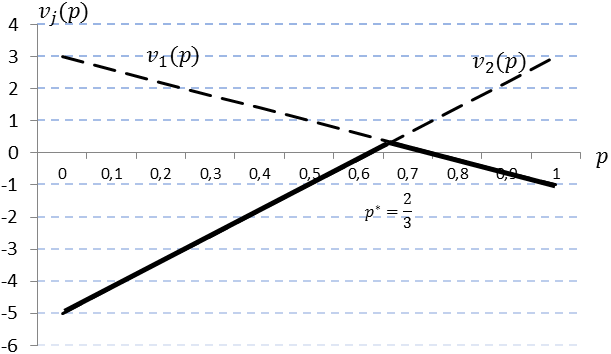
а) гарантированный выигрыш первого игрока в зависимости от его смешанной стратегии

б) верхн€€ граница проигрыша второго игрока в зависимости от его смешанной стратегии
–ис. 1.1. Ц √арантированный выигрыш первого игрока и верхн€€ граница проигрыша второго игрока в игре Ђ”гадывание монетыї в зависимости от их смешанных стратегийї
¬торой игрок так выбирает свои стратегии, чтобы обеспечить первому минимальный выигрыш:  . Ёта функци€ отмечена на рисунке 1.1. а) жирной линией.
. Ёта функци€ отмечена на рисунке 1.1. а) жирной линией.
¬торой игрок в любом случае заставит первого выиграть как можно меньше, т. е. в рассматриваемой игре:
- при  где
где  соответствует максимуму функции
соответствует максимуму функции 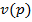 , второй игрок будет выбирать свою вторую стратегию, и первый игрок будет выигрывать
, второй игрок будет выбирать свою вторую стратегию, и первый игрок будет выигрывать 
- при  второй игрок будет выбирать первую стратегию, и первый игрок будет выигрывать
второй игрок будет выбирать первую стратегию, и первый игрок будет выигрывать  .
.
Ќаилучший дл€ первого игрока выбор соответствует 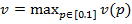 , т. е.
, т. е.  , при этом цена игры равна
, при этом цена игры равна  .
.
¬ рассматриваемом примере  , определ€ема€ из услови€
, определ€ема€ из услови€  или
или  .
.
“аким образом, оптимальной смешанной стратегией первого игрока €вл€етс€ стратеги€  , при этом цена игры равна
, при этом цена игры равна  . ¬не зависимости от того, какую стратегию выберет второй игрок, первый игрок будет выигрывать в среднем за большое число партий по
. ¬не зависимости от того, какую стратегию выберет второй игрок, первый игрок будет выигрывать в среднем за большое число партий по  руб. за одну партию.
руб. за одну партию.
Ќайдем оптимальную смешанную стратегию второго игрока.
ѕусть второй игрок выбирает первую стратегию с веро€тностью  , а вторую Ц с веро€тностью
, а вторую Ц с веро€тностью  , т. е. вектор смешанной стратегии второго игрока имеет вид
, т. е. вектор смешанной стратегии второго игрока имеет вид  .
.
“огда проигрыш второго игрока, представленный на рисунке 1.1 б), равен:
 , если первый игрок выбирает свою первую стратегию,
, если первый игрок выбирает свою первую стратегию,
 , если первый игрок выбирает свою вторую стратегию.
, если первый игрок выбирает свою вторую стратегию.
Ќаилучшее с точки зрени€ второго игрока значение  определ€етс€ из услови€
определ€етс€ из услови€ 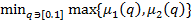 .
.
ак видно из рис. 1.1, б, в данном случае  , откуда
, откуда  .
.
ѕоэтому оптимальна€ смешанна€ стратеги€ второго игрока равна  .
.
–ешение игры 
ѕриписав первой строке веро€тность  , а второй строке Ц веро€тность
, а второй строке Ц веро€тность  , получим n линейных зависимостей. »зобразим их графики.
, получим n линейных зависимостей. »зобразим их графики.
¬озьмем нижнюю огибающую, т.е. такую ломаную из отрезков построенных пр€мых, что вс€ картинка лежит выше этой ломаной. “очка с наибольшей координатой  дает нам
дает нам  (перва€ координата) и цену игры
(перва€ координата) и цену игры  (втора€ координата).
(втора€ координата).
ѕусть это точка пересечени€ i -й и j -й пр€мых. “огда припишем i -му столбцу веро€тность  , а j -му столбцу Ц веро€тность
, а j -му столбцу Ц веро€тность  . ¬сем остальным столбцам припишем нулевые веро€тности. Ќаходим
. ¬сем остальным столбцам припишем нулевые веро€тности. Ќаходим  и
и  .
.
ѕример 1.6. Ќайдем решение матричной игры:
 .
.
ѕервый столбец доминирует над третьим столбцом. ѕоэтому отбросим третий столбец. ¬еро€тность 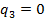 . ѕолучим матрицу
. ѕолучим матрицу  .
.
ѕрипишем строка веро€тности  и
и 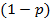 соответственно.
соответственно.
 .
.
ѕолучим линейные зависимости  ;
; 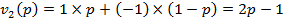 ;
;  .
.
»зобразим их графики.  .
.

–ис. 1.2 Ц √рафики функций линейных зависимостей  ,
,  ,
,  и нижней огибающей ломаной пр€мой
и нижней огибающей ломаной пр€мой
¬озьмем нижнюю огибающую. Ёто ломана€ ABC. “очка B Ц это точка пересечени€ пр€мых (1) и (3). ѕоэтому припишем первому столбцу веро€тность  , а третьему столбцу Ц веро€тность
, а третьему столбцу Ц веро€тность  . ¬сем остальным столбцам припишем нулевые веро€тности. Ќайдем координаты точки B.
. ¬сем остальным столбцам припишем нулевые веро€тности. Ќайдем координаты точки B.
 ,
,  (веро€тность применени€ игроком ј своей первой стратегии),
(веро€тность применени€ игроком ј своей первой стратегии),
 (веро€тность применени€ игроком ј своей второй стратегии).
(веро€тность применени€ игроком ј своей второй стратегии).
|
|
|
¬се цифры игрок ј делит на полноценные Ђп€теркиї. ѕервые две цифры относ€тс€ к первой стратегии, а три последние Ц ко второй стратегии: перва€ стратеги€ (1,2,6,7) и втора€ стратеги€ (3,4,5,8,9,0). ѕеред своим очередным ходом игрок ј смотрит в таблицу случайных чисел. ≈сли Ђвыпадаетї 1,2,6,7, то он играет первую стратегию; если Ђвыпадаетї 3,4,5,8,9,0, то он играет вторую стратеги. ÷ена игры 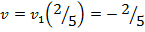 .
.
ѕримечание. ћатематическа€ функци€ —Ћ„»— мастера формул  пакета Excel возвращает случайное число;
пакета Excel возвращает случайное число;  математические
математические  —Ћ„»—
—Ћ„»—  ќ . ” этой функции не оргументов. ќ . ѕосле этого в €чейке по€витс€ дес€тична€ дробь из интервала (0,1). »сследователь берет нужное число знаков после зап€той. ѕосле нажати€ клавиши F9 дес€тична€ дробь в €чейке изменитс€.
ќ . ” этой функции не оргументов. ќ . ѕосле этого в €чейке по€витс€ дес€тична€ дробь из интервала (0,1). »сследователь берет нужное число знаков после зап€той. ѕосле нажати€ клавиши F9 дес€тична€ дробь в €чейке изменитс€.
Ќайдем ненулевые веро€тности выбора стратегий игроком B.
»спользуем матрицу
 0
0 
 .
.
»меем 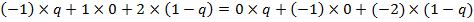 , т.е.
, т.е.  ,
,  .
.
ƒл€ игрока ј  ; дл€ игрока B
; дл€ игрока B  .
.
«адача: Ќайти решение матричной игры  ќтвет: v=4/11,
ќтвет: v=4/11,

ѕример 1.7. –ассмотрим игру с платежной матрицей

“ребуетс€ найти оптимальные смешанные стратегии игроков.
–ешение. ѕ роверим, имеет ли данна€ игра седловую точку в чистых стратеги€х.
Ќижн€€ цена игры 
¬ерхн€€ цена игры 
т. е.  , значит, седловой точки в чистых стратеги€х в игре нет.
, значит, седловой точки в чистых стратеги€х в игре нет.
ѕусть первый игрок играет со смешанной стратегией  . ќбозначим
. ќбозначим  ожидаемый выигрыш первого игрока, если второй игрок при этом выберет свою j -ю стратегию.
ожидаемый выигрыш первого игрока, если второй игрок при этом выберет свою j -ю стратегию.
¬ рассматриваемом примере
 ,
,
 ,
,
 ,
,
 .
.
√рафики этих функций построены на рис.1.3.
¬торой игрок так выбирает свои стратегии, чтобы обеспечить первому минимальный выигрыш:  . Ёта функци€ отмечена на рис. 1.3 жирной линией.
. Ёта функци€ отмечена на рис. 1.3 жирной линией.
ѕри  , где
, где  определ€етс€ из услови€
определ€етс€ из услови€  второй игрок будет выбирать свою вторую стратегию, и первый игрок будет выигрывать
второй игрок будет выбирать свою вторую стратегию, и первый игрок будет выигрывать 
ѕри  , второй игрок будет выбирать первую стратегию, и первый игрок будет выигрывать
, второй игрок будет выбирать первую стратегию, и первый игрок будет выигрывать  .
.
Ќаилучший дл€ первого игрока выбор при этом соответствует 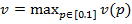 .
.
–ис. 1.3. √арантированный выигрыш первого игрока в примере 1.4 при различном выборе смешанной стратегии
“аким образом, оптимальной смешанной стратегией первого игрока €вл€етс€ стратеги€  при этом цена игры равна
при этом цена игры равна  . ¬еличина
. ¬еличина  получаетс€ путем подстановки величины
получаетс€ путем подстановки величины  в уравнени€
в уравнени€  ,
,  ,
,
¬торой игрок, действу€ разумно, никогда не будет выбирать третью и четвертую стратегии, увеличивающие выигрыш первого игрока, поэтому вектор оптимальной смешанной стратегии второго игрока имеет вид  .
.
“огда проигрыш второго игрока равен:
 , если первый игрок выбирает свою первую стратегию,
, если первый игрок выбирает свою первую стратегию,
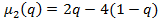 , если первый игрок выбирает свою вторую стратегию.
, если первый игрок выбирает свою вторую стратегию.
«начение 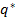 определ€етс€ из услови€
определ€етс€ из услови€  , оно равно
, оно равно  .
.
—ледовательно, оптимальна€ смешанна€ стратеги€ второго игрока равна  . ≈сли подставить
. ≈сли подставить  в уравнени€
в уравнени€  ,
, 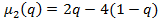 , получим цену игры
, получим цену игры  .
.
–ешение игры 
ѕриписав первому столбцу веро€тность  , а второму столбцу Ц веро€тность
, а второму столбцу Ц веро€тность  , получим
, получим  линейных зависимостей. »зобразим их графики.
линейных зависимостей. »зобразим их графики.
¬озьмем верхнюю огибающую, т.е. такую ломаную из отрезков построенных пр€мых, что вс€ картинка лежит ниже этой ломаной. “очка с наименьшей координатой  дает нам
дает нам  (перва€ координата) и цену игры
(перва€ координата) и цену игры  (втора€ координата).
(втора€ координата).
ѕусть это точка пересечени€ i -й и j -й пр€мых. “огда припишем i -й строке веро€тность  , а j -й строка веро€тность
, а j -й строка веро€тность 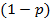 . ¬сем остальным строкам припишем нулевые веро€тности. Ќаходим
. ¬сем остальным строкам припишем нулевые веро€тности. Ќаходим  и
и 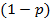 .
.
ѕример 1.8. Ќайти решение матричной игры
 .
.
ѕрипишем столбцам веро€тности  и
и  соответственно:
соответственно:


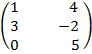
ѕолучим линейные зависимости  (1),
(1),  (2),
(2),  (3).
(3).
»зобразим их графики.  .
.
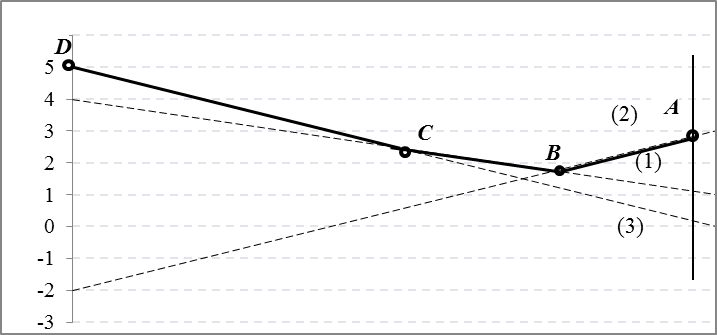
¬озьмем верхнюю огибающую. Ёто ломана€ ABCD. “очка ¬ Ц это точка с наименьшей второй координатой на этой огибающей. “очка ¬ Ц это точка пересечени€ пр€мых (1) и (2). ѕоэтому припишем первой строке веро€тность p, а второй строке Ц веро€тность 1 Ц p. ¬сем остальным строкам припишем нулевые веро€тности. Ќайдем координаты точки ¬.
4 Ц 3 q = 5 q Ц 2, q =  (веро€тность применени€ игроком ¬ своей первой стратегии), 1 Ц q =
(веро€тность применени€ игроком ¬ своей первой стратегии), 1 Ц q =  (веро€тность применени€ игроком ¬ своей второй стратегии). ¬се цифры игрок ¬ делит на полноценные Ђчетверкиї. ѕервые три цифры относ€тс€ к первой стратегии, а последн€€ Ц ко второй стратегии: перва€ стратеги€ (1, 2, 3, 5, 6, 7) и втора€ стратеги€ (4, 8). ѕеред своим очередным ходом игрок ј смотрит в таблицу случайных чисел. ≈сли Ђвыпадаетї 4, 8, то он играет вторую стратегию. ÷ена игры v = w
(веро€тность применени€ игроком ¬ своей второй стратегии). ¬се цифры игрок ¬ делит на полноценные Ђчетверкиї. ѕервые три цифры относ€тс€ к первой стратегии, а последн€€ Ц ко второй стратегии: перва€ стратеги€ (1, 2, 3, 5, 6, 7) и втора€ стратеги€ (4, 8). ѕеред своим очередным ходом игрок ј смотрит в таблицу случайных чисел. ≈сли Ђвыпадаетї 4, 8, то он играет вторую стратегию. ÷ена игры v = w  =
=  . ÷ифры 0 и 9 игнорируютс€.
. ÷ифры 0 и 9 игнорируютс€.
|
|
|
Ќайдем решение дл€ игрока ј: 
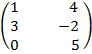 .
.
 , то есть p =
, то есть p =  , 1 ‑ p =
, 1 ‑ p =  . ƒл€ игрока ј p * = (
. ƒл€ игрока ј p * = ( дл€ игрока ¬ q* = (
дл€ игрока ¬ q* = (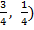 .
.
«адача: Ќайти решение матричной игры 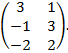 ќтвет:
ќтвет:  ,
, 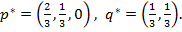
¬ данной лекции были рассмотрены два примера матричных игр, в которых у первого игрока ровно две стратегии, а у второго игрока произвольное количество стратегий. “акие игры можно решить графическим способом.
–азберем теорему, дающую способ решени€ матричных игр, в которых и у первого, и у второго игрока произвольное количество стратегий. ¬ общем случае люба€ матрична€ игра с произвольным числом стратегий у игроков может быть сведена к паре взаимно двойственных задач линейного программировани€, и эти задачи имеют оптимальные решени€.
“еорема. ¬ любой матричной игре у игроков есть оптимальные смешанные стратегии.
ƒоказательство. ѕусть рассматриваетс€ игра с платежной матрицей A (1.1), все элементы которой строго положительны;  и
и  Ч смешанные стратегии первого и второго игрока.
Ч смешанные стратегии первого и второго игрока.
ћатематическое ожидание выигрыша первого игрока  при любом выборе игроками своих смешанных стратегий р и q будет положительным, так как все элементы платежной матрицы положительны, среди неотрицательных
при любом выборе игроками своих смешанных стратегий р и q будет положительным, так как все элементы платежной матрицы положительны, среди неотрицательных  есть хот€ бы одно строго положительное число и среди неотрицательных
есть хот€ бы одно строго положительное число и среди неотрицательных 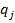 также есть хот€ бы одно строго положительное.
также есть хот€ бы одно строго положительное.
ѕусть первый игрок выбирает такую стратегию р, чтобы математическое ожидание его выигрыша независимо от того, какую стратегию выберет второй игрок, было не меньше некоторой гарантированной величины r (нижн€€ цена игры  , поскольку все платежи
, поскольку все платежи  , r не меньше
, r не меньше  , поэтому
, поэтому  ):
):
 (1.2)
(1.2)
ѕри этом  ;
; 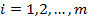 ;
; 
¬ведем новые обозначени€
 ,
, 
и разделим все неравенства системы (1.2) на положительное число r, получим следующую систему:
 (1.3)
(1.3)
ѕри этом  ;
; 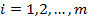 ;
; 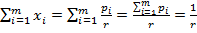 .
.
≈сли бы  , то переход от (1.2) к (1.3) был бы невозможен, т.к. при делении неравенства на отрицательное число знак мен€етс€ на противоположный, а на нуль делить нельз€.
, то переход от (1.2) к (1.3) был бы невозможен, т.к. при делении неравенства на отрицательное число знак мен€етс€ на противоположный, а на нуль делить нельз€.
÷ель первого игрока Ц максимизировать свой гарантированный выигрыш r или, соответственно, минимизировать величину  .
.
—ледовательно, приходим к задаче линейного программировани€ дл€ первого игрока:
 ,
,
 ,
,  (1.4)
(1.4)
 ;
; 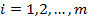
јналогичные рассуждени€ с позиции второго игрока привод€т к задаче линейного программировани€, двойственной к задаче дл€ первого игрока:
 ,
,
 ,
, 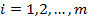 (1.5)
(1.5)
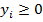 ;
; 
ѕоскольку все  , можно подобрать такие достаточно большие положительные числа
, можно подобрать такие достаточно большие положительные числа  , чтобы дл€ всех
, чтобы дл€ всех  выполн€лись неравенства
выполн€лись неравенства  .
.
Ќапример,  ,
, 
—ледовательно, задача (1.4) имеет допустимое решение.
ƒопустимым решением задачи (1.5) €вл€етс€, очевидно, нулевой вектор.
Ћекци€ 3. ћатричные игры (продолжение)
“ак как кажда€ из пары двойственных задач (1.4) и (1.5) имеет допустимое решение, то согласно теории двойственных задач линейного программировани€ обе эти задачи имеют некоторые оптимальные решени€  и
и 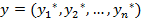 при этом оптимальные значени€ целевых функций данных задач равны:
при этом оптимальные значени€ целевых функций данных задач равны:
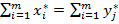 .
.
ѕокажем, что цена игры  , а оптимальные смешанные стратегии игроков равны соответственно:
, а оптимальные смешанные стратегии игроков равны соответственно:


ƒействительно, пусть  и
и  Ц произвольные смешанные стратегии игроков, тогда
Ц произвольные смешанные стратегии игроков, тогда

 (1.6)
(1.6)

=  (1.7)
(1.7)

 (1.8)
(1.8)
»з (1.6) следует, что  , из (1.7) следует, что
, из (1.7) следует, что  , а из (1.8) следует, что одновременно
, а из (1.8) следует, что одновременно
|
|
|
 (так как
(так как  )
)
и
 (так как
(так как  ),
),
«начит  .
.
»так,  ,
,  ,
,  , поэтому
, поэтому
 .
.
“аким образом, пара  образует седловую точку данной игры в смешанных стратеги€х, и
образует седловую точку данной игры в смешанных стратеги€х, и  Ц цена данной игры.
Ц цена данной игры.
≈сли же в платежной матрице 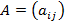 есть отрицательные элементы или нули, то можно добавить ко всем элементам матрицы одно и то же достаточно большое положительное число b, так чтобы все элементы матрицы
есть отрицательные элементы или нули, то можно добавить ко всем элементам матрицы одно и то же достаточно большое положительное число b, так чтобы все элементы матрицы 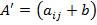 были положительными.
были положительными.
ќбозначим  математическое ожидание выигрыша первого игрока в игре с платежной матрицей
математическое ожидание выигрыша первого игрока в игре с платежной матрицей 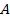 , а
, а  Ц математическое ожидание выигрыша первого игрока в игре с платежной матрицей
Ц математическое ожидание выигрыша первого игрока в игре с платежной матрицей  .
.
ѕри этом
 ,
,
игра с платежной матрицей  имеет седловую точку
имеет седловую точку  в смешанных стратеги€х:
в смешанных стратеги€х:

или
 ,
,
откуда
 ,
,
т. е. игра с платежной матрицей 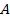 также имеет седловую точку
также имеет седловую точку  в смешанных стратеги€х, а цена игры с матрицей
в смешанных стратеги€х, а цена игры с матрицей  равна
равна
 .
.
ѕример 1.8. “ребуетс€ найти оптимальные смешанные стратегии в игре из примера 1.7, свед€ эту игру к паре взаимно двойственных задач линейного программировани€.
–ешение. ќт платежной матрицы

путем добавлени€ положительного числа  перейдем к матрице,
перейдем к матрице,

все элементы которой положительны.
—ведем данную матричную игру к паре двойственных задач линейного программировани€ (согласно теореме 1.2):


 ,
, 


 ,
,  ,
,  ,
,  .
.
–ешаем уравнени€ из первой системы уравнений первое и второе, так как третье и четвертое дает отрицательные значени€ х, получаем:
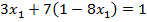


 .
.
“ак как выбрали в системе x первые два уравнени€, то в системе y занул€ютс€  и
и  .
.



 .
.
ѕоскольку оптимальные решени€ этих задач равны  и
и  , оптимальные смешанные стратегии игроков
, оптимальные смешанные стратегии игроков
 (
(
и
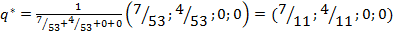 ,
,
а цена игры
 .
.






