Решения в условиях определенности, риска и неопределенности

Введение

Решение – выбор альтернативы.

В управлении принятие решений является систематизированным процессом.

Решения, принимаемые руководителем для выполнения обязанностей, обусловленных занимаемой должностью называют организационными решениями. Организационные решения квалифицируют как запрограммированные и незапрограммированные.

Запрограммированным решением называют решение, принятое как результат реализации определенной последовательности действий или шагов. Как правило, число возможных альтернатив ограничено, и выбор должен быть сделан в пределах направлений, заданных предприятием.

Незапрограммированные решения – решения, принимаемые в ситуациях, которые в определенной степени новы, внутренне не структурированы или сопряжены с неизвестными факторами.

Очень редко решения, принимаемые руководителем, могут рассматриваться как запрограммированные или незапрограммированные в чистом виде. Даже самое структурированное решение подразумевает некоторую личную инициативу лица, принимающего решение, а для принятия незапрограммированного решения почти всегда могут быть использованы моменты методологии принятия запрограммированных решений.

Процесс принятия решений – процесс психологический. Решения варьируются от спонтанных до высокологичных. Поэтому процессы принятия решений делятся на имеющий интуитивный, основанный на суждениях и рациональный характер, хотя решение редко относится к какой либо одной категории.

Интуитивное решение – это решение, принятое только на основе того, что руководитель имеет ощущение того, что оно правильно.

Рациональное решение – это решение, обоснованное с помощью объективного аналитического процесса. Кроме всего вышеперечисленного на процесс принятия решений влияют такие факторы как личностные оценки руководителя, среда принятия решений, информационные ограничения, поведенческие ограничения и т.д.

Решение принимается в условиях определенности, когда руководитель может с точностью определить результат каждого альтернативного решения, возможного в данной ситуации. Уровень определенности при принятии решений зависит от внешней среды. Он увеличивается при наличии твердой правовой базы, ограничивающей количество альтернатив и снижающей уровень риска.

К решениям, принимаемым в условиях риска, относятся такие решения, результаты которых не являются определенными, но вероятность каждого возможного результата можно определить. Вероятность определяется в промежутке от 0 до 1 и представляет собой степень возможности совершения данного события. Сумма вероятностей всех альтернатив должна быть равна единице.

Риск при принятии решений может быть различным. В экономике различают несколько типов риска: страховой, валютный, кредитный и т.д. В зависимости от типа риска, вероятность его можно определить математическими и статистическими методами.

Наиболее желательный способ определения вероятности – объективность. Вероятность объективна, когда ее можно определить математическими методами или путем статистического анализа накопленного опыта. Вероятность может быть объективно определена, если поступит достаточно релевантной информации для того, чтобы прогноз оказался статистически достоверным.

Во многих случаях предприятие не располагает достаточной информацией для объективной оценки вероятности. В таком случае часто руководители используют суждения о возможности совершения альтернатив с той или иной субъективной или предполагаемой вероятностью.

Решение принимается в условиях неопределенности, когда невозможно оценить вероятность потенциальных результатов. Это имеет место, когда требующие учета факторы настолько новы и сложны, что невозможно получить достаточно релевантной информации, позволяющей объективно определить вероятность, либо имеющаяся ситуация не подчиняется известным закономерностям. Поэтому вероятность определенного последствия невозможно предсказать с достаточной степенью достоверности. Неопределенность характерна для некоторых решений, принимаемых в быстро меняющихся условиях.

Для принятия оптимальных решений необходимо использовать научный метод. В науке управления научный метод подразумевает наличие определенной структуры процесса принятия решений и использование различных методов и моделей принятия решений.

Модель – это представление объекта, системы или процесса в форме отличной от оригинала, но сохраняющей основные его характеристики. В науке управления используются следующие модели принятия решений:

- теория игр;

- модели теории очередей;

- модели управления запасами;

- модель линейного программирования;

- транспортные задачи;

- имитационное моделирование;

- сетевой анализ;

- экономический анализ.

Теория игр. Данный метод служит для моделирования оценки воздействия принятого решения на конкурентов. Изначально была разработана военными с тем, чтобы в стратегии учесть возможные действия противника. В бизнесе игровые модели используются для прогнозирования реакции конкурентов на изменение цен, модификацию и освоение новой продукции, предложения дополнительного обслуживания и т.д. Теория игр используется реже, чем другие модели, так как ситуации в реальном мире очень сложны и часто меняются.

Модели теории очередей, или модели оптимального обслуживания используются для определения оптимального числа каналов обслуживания по отношению к потребности в них. Применяется в различных ситуациях, где есть клиенты и пункты их обслуживания (резервирование билетов по телефону, обслуживание клиентов в банке, количество разгрузочных площадок на складах и т.д.). Используются для уравновешивания расходов на дополнительные каналы обслуживания и потерь от обслуживания на уровне ниже оптимального.

Модели управления запасами используются для определения времени размещения заказов на ресурсы и их количества, а также массы готовой продукции на складах. Цель данной модели оптимизация запасов на предприятии. Чрезмерное их накопление хотя помогает избежать потерь, обусловленных их нехваткой, во многих случаях сводит к минимуму издержки на размещение заказов, так как они размещаются в больших количествах, но также ведет к дополнительным издержкам на хранение, перегрузку, потери от порчи, уменьшение оборотных средств, что уменьшает мобильность предприятия в принятии решений при возникновении новой ситуации на рынке.

Модели линейного программирования применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Данный вид модели наиболее распространен на промышленных предприятиях. Он заключается в том, что помогает максимизировать прибыль при наличии одного нескольких ресурсов, каждый из которых используется для производства нескольких видов товара. Обычно при решении оптимизации данного типа моделей обычно используется Симплекс-метод.

Транспортные задачи – это задачи, с помощью которых оптимизируется доставка ресурсов при наличии нескольких пунктов отправки и нескольких пунктов получения при различной стоимости доставки в различные пункты. Является частным видом задач линейного программирования.

Имитационное моделирование означает процесс создания модели и ее экспериментальное использование для определения изменений реальной ситуации. Имитация используется в ситуациях, слишком сложных для математических методов типа линейного программирования. Экспериментируя на модели системы, можно установить, как она будет реагировать на определенные изменения или события, в то время, когда отсутствует возможность наблюдать эту систему в реальности.

Сетевой анализ. Из сетевого анализа в основном используется теория графов. Теория графов позволяет составлять оптимальные графики осуществления различных проектов. Это позволяет минимизировать как время осуществления проекта, так и затраты по нему.

Экономический анализ один из самых распространенных методов моделирования, хотя он и не воспринимается как моделирование. Экономический анализ вбирает в себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Экономический анализ включает в себя анализ безубыточности, определение прибыли на инвестированный капитал, величину чистой прибыли на данный момент времени и т.д. эти модели широко применяются в бухгалтерском и финансовом учете.

При принятии решения вне зависимости от применяемых моделей существуют некоторые правила принятия решений. Правило принятия решения – это критерий, по которому выносится суждение об оптимальности данного конкретного исхода. Существует два типа правил. Один не использует численные значения вероятных исходов, второй – использует данные значения.

Методы принятия решений:

- платежная матрица;

- дерево решений;

- методы прогнозирования.

Платежная матрица – один из методов статистической теории решений, оказывающий помощь руководителю в выборе одного из нескольких вариантов. В самом общем виде матрица означает, что платеж зависит от определенных событий, которые фактически совершаются. Если событие или состояние природы не случается на деле, платеж неизменно будет другим.

Руководитель должен иметь возможность объективно оценить вероятность релевантных событий и рассчитать ожидаемое значение такой вероятности.

Вероятность прямо влияет на определение ожидаемого значения – основного понятия платежной матрицы. Ожидаемое значение альтернативы или варианта – это сумма возможных значений, умноженных на соответствующие вероятности.

Дерево решений – метод науки управления – схематичное представление проблемы принятия решений – используется для выбора наилучшего направления действий из имеющихся вариантов.

Метод дерева решений может применяться как в ситуациях, в которых применяется платежная матрица, так и в более сложных ситуациях, в которых результаты одного решения влияют на последующие решения. То есть дерево решений – удобный метод для принятия последовательных решений.

Методы прогнозирования. Прогнозирование – метод, в котором используется как накопленный в прошлом опыт, так и текущие допущения насчет будущего с целью его определения. Результат качественного прогнозирования может служить основой планирования. Существуют различные разновидности прогнозов: экономические прогнозы, прогнозы развития технологии, прогнозы развития конкуренции, прогнозы на основе опросов и исследований, социальное прогнозирование.

Все типы прогнозов используют различные методы прогнозирования.

Методы прогнозирования включают в себя:

- неформальные методы;

- количественные методы;

- качественные методы.

Неформальные методы включают в себя следующие виды информации:

1. Вербальная информация – это наиболее часто используемая информация для анализа внешней среды. Сюда относят информацию из радио- и телепередач, от поставщиков, от потребителей, от конкурентов, на различных совещаниях и конференциях, от юристов, бухгалтеров и консультантов. Данная информация легко доступна, затрагивает все основные факторы внешнего окружения, представляющие интерес для предприятия. Однако она очень изменчива и нередко неточна.

2. Письменная информация – это информация из газет, журналов, информационных бюллетеней, годовых отчетов. Эта информация обладает теми же достоинствами и недостатками, что и вербальная информация.

3. Промышленный шпионаж.

Количественные методы прогнозирования используются исходя из предположения, что деятельность в прошлом имела определенную тенденцию, которая может продолжиться и в будущем, и когда достаточно информации для выявления таких тенденций. К количественным методам относятся:

1. Анализ временных рядов. Он основан на допущении, согласно которому случившееся в прошлом дает достаточно хорошее приближение к оценке будущего. Проводится с помощью таблицы или графика.

2. Причинно-следственное (казуальное) моделирование. Наиболее математически сложный количественный метод прогнозирования. Используется в ситуациях с более чем одной переменной. Казуальное моделирование – прогнозирование путем исследования статистической зависимости между рассматриваемым фактором и другими переменными. Из казуальных прогностических моделей самыми сложными являются эконометрические модели, разработанные с целью прогнозирования динамики экономики.

Качественные методы прогнозирования подразумевает прогнозирование будущего экспертами. Существует четыре наиболее распространенных метода качественного прогнозирования:

1. Мнение жюри – соединение и усреднение мнений экспертов в релевантных сферах. Неформальная разновидность данного метода – «мозговой штурм».

2. Совокупное мнение сбытовиков. Мнение дилеров или предприятий сбыта очень ценно, так как они имеют дело непосредственно с конечными потребителями и знают их потребности.

3. Модель ожидания потребителя – прогноз, основанный на результатах опроса клиентов предприятия.

4. Метод экспертных оценок. Он представляет собой процедуру, позволяющую группу экспертов приходить к согласию. По данному методу эксперты из различных областей заполняют опросник по данной проблеме. Затем им дают опросники, заполненные другими экспертами, и просят пересмотреть свое мнение либо аргументировать первоначальное. Процедура проходит 3-4 раза, пока в результате не будет выработано общее решение. Причем все опросники анонимны, как и анонимны сами эксперты, то есть эксперты не знают, кто еще входит в группу.

 

ТЕМА 1. МАТРИЧНЫЕ ИГРЫ

Лекция 1. Матричные игры

В экономике и управлении встречаются ситуации, когда сталкиваются две и более стороны, преследующие различные цели. Причем результат, полученный каждой из сторон при реализации определенной стратегии, зависит от действий других сторон. Такие ситуации называются конфликтными.

Примеры: борьба фирм за рынок сбыта, аукцион, спортивные состязания, военные операции, парламентские выборы при наличии нескольких кандидатов, карточные игры.

Простейшим примером конфликтной ситуации является игра с нулевой суммой или антагонистическая игра, в которой выигрыш одной стороны конфликта в точности совпадает с проигрышем другой стороны.

Рассмотрим конфликт двух участников с противоположными интересами, математической моделью которого является игра с нулевой суммой. Участники игры – лица, принимающие решения, - называются игроками. Стратегия игрока – осознанный выбор одного из множества возможных вариантов его действий. Рассмотрим конечные игры, в которых множества стратегий игроков конечны: стратегии первого игрока пронумеруем числами от 1 до m, стратегии второго игрока – от 1 до n.

Если первый игрок выбрал свою i -ую стратегию, а второй игрок – свою j -тую стратегию, то результатом такого совместного выбора будет платеж 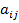второго игрока первому. В качестве платежа может выступать не только денежная сумма, но и оценка полезности результата выбора игроками своих стратегий i и j. Таким образом, конечная игра с нулевой суммой однозначно определяется матрицей

, (1.1)

которая называется платежной матрицей или матрицей выигрышей. Строки этой матрицы соответствуют стратегиям первого игрока, а столбцы – стратегиям второго игрока. Конечные игры с нулевой суммой называются матричными, т.к. целиком определяются своими платежными матрицами.

Игра происходит партиями. Партия игры состоит в том, что игроки одновременно называют свой выбор: первый игрок называет некоторый номер строки матрицы А, а второй игрок - некоторый номер столбца этой матрицы (по своему выбору или случайно). После этого происходит «расплата». Пусть первый игрок назвал номер i, а второй – j. Тогда второй игрок платит первому сумму 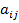, и партия игры заканчивается. Если , то это означает, что при выборе первым игроком i -й стратегии, а вторым – j -й, выигрывает первый игрок; если , то выигрывает второй игрок. Цель каждого игрока – выиграть как можно большую сумму в результате большого числа партий.

Смысл названий «конфликт с противоположными интересами» и «игра с нулевой суммой» состоит в том, что выигрыш каждого из игроков противоположен выигрышу противника, т.е. сумма выигрышей игроков равна нулю.

Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистый стратегий, у второго – n.

При анализе игр противник считается сильным, т.е. разумным.

Рассмотрим описанную конфликтную ситуацию с точки зрения первого игрока. Если первый игрок выбирает свою i -ую стратегию или i -ую строку матрицы А, то второй игрок, будучи разумным, выберет такую стратегию j, которая обеспечит ему наибольший выигрыш, а первому игроку соответственно наименьший, т.е. второй игрок выберет такой столбец j матрицы А, в котором платеж 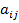второго игрока первому минимален. Перебирая все свои стратегии i =1, 2, … m и первый игрок выбирает ту из них, при которой второй игрок, действуя максимально разумно, заплатит ему наибольшую сумму.

Величина называется нижней ценой игры, а соответствующая ей стратегия первого игрока – максиминной.

Аналогичные рассуждения с точки зрения второго игрока определяют верхнюю цену игры и соответствующую ей минимаксную стратегию второго игрока.

Нижняя цена игры представляет собой максимальный гарантированный выигрыш первого игрока, т.е. первый игрок обеспечивает себе выигрыш не меньше , а верхняя цена игры – минимальный гарантированный проигрыш второго игрока, т.е. второй игрок обеспечивает себе проигрыш не больше или выигрыш не меньше (- .

Если , то говорят, что игра имеет седловую точку в чистых стратегиях, общее значение и называется ценой игры и обозначается . При этом стратегии игроков, соответствующие седловой точке, называются оптимальными чистыми стратегиями, т.к. эти стратегии являются наиболее выгодными сразу для обоих игроков, обеспечивая первому – гарантированный выигрыш не менее v, а второму – гарантированный проигрыш не более – v, Отклонение от этих стратегий не выгодно.

Пример 1.1. В платежной матрице

Указано, какую долю рынка выиграет предприятие у своего единственного конкурента, если оно будет действовать согласно каждой из возможных трех стратегий, а конкурент – согласно каждой из своих возможных трех стратегий. Определить, имеет ли данная игра седловую точку в чистых стратегиях.

Решение. Припишем справа от строк платежной матрицы минимальные элементы этих строк (соответствующие выигрышу первого игрока в том случае, когда он выберет стратегию, соответствующую данной строке, а второй игрок при этом выберет стратегию, соответствующую наилучшему для него выигрышу); под столбцами платежной матрицы напишем максимальные элементы этих столбцов (соответствующие проигрышу второго игрока в том случае, когда он выберет стратегию, соответствующую данному столбцу, а первый игрок при этом выберет стратегию соответствующую наилучшему для него выигрышу):

||

Нижняя цена игры , соответствует второй стратегии первого игрока.

Верхняя цена игры , соответствует третьей стратегии второго игрока, поэтому если первый игрок будет действовать со второй стратегией, а второй игрок – с третьей, то игроки могут гарантировать себе: первый – выигрыш не менее рынка, а второй – что первый выиграет не более рынка.

Таким образом, данная игра имеет седловую точку в чистых стратегиях (в платежной матрице седловая точка обведена рамкой), при этом оптимальная чистая стратегия первого игрока – вторая, оптимальная чистая стратегия второго игрока – третья, а цена игры равна .

Если первый игрок будет следовать своей оптимальной чистой стратегии (второй), а второй игрок отклонится от своей оптимальной чистой стратегии (третьей), то он ухудшит свое положение и будет проигрывать не 30%, а 50% или 40% рынка. Первому игроку также невыгодно отклоняться от своей второй стратегии, если второй игрок будет придерживаться третьей.

Матричная игра не всегда имеет седловую точку в чистых стратегиях.

Пример 1.2 Игра «Угадывание монеты». Правила игры следующие: первый игрок прячет в кулаке одну из двух монет – 1 руб. или 5 руб. – по своему выбору и незаметно от второго игрока, а второй игрок пытается угадать, какая монета спрятана. Если угадывает, то получает эту монету, если нет, то платит первому игроку 3 руб. Доказать, что данная игра не имеет седловой точки в чистых стратегиях.

Решение. Платежная матрица имеет вид:

Нижняя цена игры .

Верхняя цена игры .

Таким образом, и седловой точки в чистых стратегиях в игре нет.

Теорема. В любой матричной игре нижняя цена не превосходит верхнюю цену игры: .

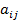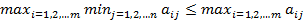Доказательство. Любой элемент платежной матрицы не меньше минимального элемента i -й строки: и не больше максимального элемента j -го столбца: . Таким образом, , откуда . Левая часть этого неравенства зависит от номера строки i, а правая часть не зависит, поэтому для любого столбца j или (одновременно для всех j). Но это означает, что или , что и требовалось доказать.

Рассмотрим ситуацию, когда нижняя цена игры строго меньше верхней, т.е. когда в игре отсутствует седловая точка.

Смешанной стратегией первого игрока называется вектор , где все (), а . При этом – вероятность, с которой первый игрок выбирает свою i -ую стратегию. Аналогично определяется смешанная стратегия

второго игрока. Чистая стратегия также подпадает под определение смешанной – в этом случае все вероятности равны нулю, кроме одной, равной единице.

Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений, причем в качестве весового коэффициента берется вероятность соответствующего исхода, т.е. сумма произведений всех возможных значений случайной величины на их вероятности.

Предположим, что х может принимать n конкретных значений () и что вероятность получения х_i равна p_i. Тогда =

Пример. Число очков, выпадающее при бросании одной игральной кости. В данном случае возможны шесть исходов, каждый из которых имеет вероятность 1/6, поэтому

Математическое ожидание случайной величины часто называют ее средним по генеральной совокупности. Для случайной величины х это значение часто обозначается как µ.

Если игроки играют со своими смешанными стратегиями и соответственно, то математическое ожидание выигрыша первого игрока равно:

И совпадает с математическим ожиданием проигрыша второго игрока.

Стратегии и называются оптимальными смешанными стратегиями соответственно первого и второго игрока, если

.

Если у обоих игроков есть оптимальные смешанные стратегии, то пара называется решением игры (или седловой точкой в смешанных стратегиях), а число

- ценой игры.

Теорема фон Неймана. Каждая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

 

Лекция 2. Матричные игры (продолжение)