Плоское напряженное состояние

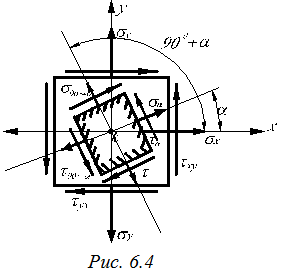
В том случае, когда задано произвольное плоское напряженное состояние с напряжениями σ_х, σ_у, τ_xy, τ_yx можно найти напряжения действующие на площадках, наклоненных под углами α и 90⁰ + α к оси х (рис.6.4).

(6.2)

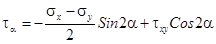(6.3)

Для напряженного состояния в точке «к» выполняется закон суммы нормальных напряжений:

σ_х + σ_у = σ_α + σ_α+90. (6.4)

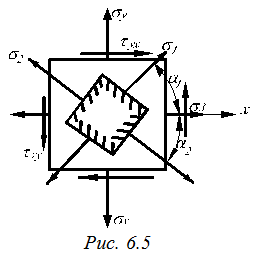В курсе сопротивление материалов важно знать значение максимальных нормальных и касательных напряжений.

На площадках, где действуют экстремальные нормальные напряжения s₁, s₂, касательные напряжения t=0. Такие площадки называются главными (рис. 6.5).

Нормальные напряжения на главных площадках называются главными напряжениями и обозначаются σ₁ и σ₂. Для них выполняются условие σ₁ > σ₂.

Главные напряжения определяются как:

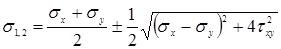(6.5)

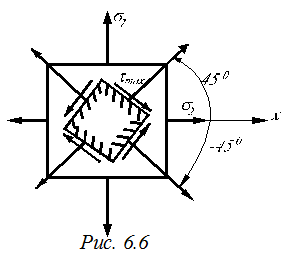Положение главных площадок находится из равенства

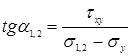(6.6)

Максимальные касательные напряжения действуют на площадках, расположенных под углом α=±45⁰ к оси х (рис.6.6):

 

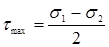(6.7)

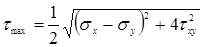(6.8)

 

 

Объемное напряженное состояние

 

Главные напряжения σ₁, σ₂, σ₃ можно получить, приравнивая определитель ∆ системы уравнений (6.9) нулю, которая получена из условий равновесия элемента

(σ_x – σ_i) l_i +τ_yх m_i + τ_zх n_i = 0

τ_xy l_i + (σ_у – σ_i) m_i + τ_zy n_i = 0 (6.9)

τ_xz l_i + τ_yz m_i +(σ_z – σ_i) = 0

Получим кубическое уравнение относительно неизвестных главных напряжений (6.10):

(6.10)

I₁, I₂, I₃ – инварианты главных напряжений, т.е. величины не зависящие от выбора исходной системы координат.

I₁ = σ_х+σ_у+σ_z. (6.11)

I₂ = σ_хσ_у +σ_уσ_z.+ σ_zσ_x – (6.12)

I₃ = σ_хσ_уσ_z – σ_х (6.13)

Из уравнения (6.10) найдем главные напряжения σ₁, σ₂, σ₃. Подставив значение одного из главных напряжений σ_i в первые два уравнения системы уравнений (6.9) и решив их совместно с геометрическим условием (6.14)

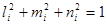(6.14)

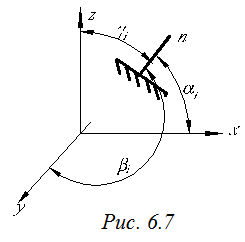
найдем величины направляющих косинусов, которые характеризуют положение главной площадки в системе координат xyz (рис. 6.7).

На площадке, нормаль к которой n_i, действует напряжение σ_i с (i =1,2,3).

cos α_i = cos(n_ix) = l_i

cos β_i = cos(n_iy) = m_i

cos γ_i = cos(n_iz) = n_i

l_i , m_i, n_i – направляющие косинусы.

Напряжения и деформации при объемном напряженном состоянии определяются из обобщенного закона Гука.

(6.15)

Выражение (6.15) представляет собой обобщенный закон Гука при объемном напряженном состоянии. При действии нормальных напряжений по граням элементарного параллелепипеда происходит изменение объема материала, которое определяется по выражению (6.16):

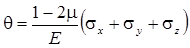(6.16)

 

Рассмотрим случай гидростатического сжатия элементарного параллелепипеда (рис. 6.8). σ_х = σ_у = σ_z.= – σ. Из уравнения (6.16) следует

(6.17)

Отсюда вытекает важный вывод, что коэффициент Пуассона μ £ 0,5, так как при сжатии элемент не может увеличивать объем.

 

 

Теории прочности

 

Элементы строительных конструкций и детали машин работают в условиях сложного напряженного состояния.

Оценка прочности элементов при одноосном напряженном состоянии производится путем эксперимента – испытания на растяжение (сжатие).

Для оценки прочности материала элемента, испытывающего сложное напряженное состояние, его сравнивают с одноосным напряженным состоянием.

При построении теорий прочности исходят из предпосылки, что два напряженных состояния считаются равнопрочными в том случае, когда при одинаковом и пропорциональном увеличении главных напряжений они становятся предельными.

Для пластичного материала предельными считаются напряжения, при которых появляются заметные остаточные (пластические) деформации. Предельные напряжения при одноосном растяжении принимаются равными пределу текучести σ_т.

Для хрупкого материала предельными считаются напряжения, которые соответствуют началу разрушения и принимаются при одноосном состоянии равным σ_в.

При построении теорий прочности связывают главные напряжения двух указанных состояний какой-либо причиной разрушения.

I теория прочности – теория наибольших нормальных напряжений

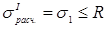(6.18)

II теория прочности – теория наибольших линейных деформаций

(6.19)

III теория прочности – теория наибольших касательных напряжений

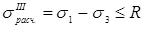(6.20)

IV теория прочности – энергетическая

(6.21)

Теория прочности Мора:

σ_расч. = σ – k σ₃ £ R (6.22)

Здесь R – расчетное сопротивление материала;

k – коэффициент, учитывающий различные сопротивления материала деформациям растяжения и сжатия.

 

Главные напряжения удовлетворяют условию: σ₁ > σ₂> σ₃.

Для пластических материалов в практике расчета строительных конструкций используется III и IV теория прочности.