Внутренние силовые факторы в поперечных сечениях бруса. Метод сечений

 

Отдельные частицы любого тела связаны внутренними силами взаимодействия, которые препятствуют внешним воздействиям деформировать тело.

В сопротивлении материалов рассматриваются только те внутренние силы, которые вызваны внешними воздействиями и не учитываются те усилия, которые имеются в естественном незагруженном состоянии.

Для определения внутренних усилий используется метод сечений. В этом случае элемент мысленно рассекается некоторой плоскостью на две части. Каждую часть элемента можно рассмотреть в равновесии под действием внешней нагрузки и внутренних сил.

Внутренние силы, распределенные по сечению, приведенные к одной точке, сводятся к главному вектору и главному моменту . Разложив главный вектор (N_z, Q_x, Q_y) и главный момент 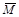(M_x, M_y, M_z) по осям координат, получим шесть внутренних силовых факторов (рис. 1.1).

Σ F_z = 0: Þ N_z – продольное усилие;

Σ F_y = 0: Þ Q_y – поперечная сила;

Σ F_x = 0: Þ Q_x – поперечная сила; (1.6)

Σ m_x = 0: Þ M_x – изгибающий момент;

Σ m_у = 0: Þ M_y – изгибающий момент;

Σ m_z = 0: Þ M_kp –крутящий момент.

Виды деформаций

 

Внутреннее усилие, действующеев элементе, определяет соответствующий вид деформации (рис. 1.2).

– растяжение (сжатие): внутреннее усилие – N_z;

 

– сдвиг: внутренние усилия – Q_y, Q_x;

 

– изгиб: внутренние усилия – M_x , M_у;

 

 

– кручение: внутренне усилие – M_кр.

 

 

Понятие о напряжениях в точке

В сечениях элемента внутренние усилия непрерывно распределены по площади поперечного сечения. На бесконечно малом элементе ∆ F площади F эти силы можно считать распределенными равномерно. Равнодействующая этих сил ∆ R приложена в центре тяжести элемента (рис. 1.3). Разложив равнодействующую ∆ R на составляющие нормальную ∆ N и касательную ∆ Q к сечению получим:

– напряжение в точке к.

= s_z – нормальное напряжение в точке к.

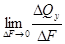= t_у – касательные напряжения в точке к.

Размерность напряжений – Н/м²=Па

Следовательно, напряжение – мера интенсивности внутренних сил, которое измеряется внутренней силой, отнесенной к единице площади сечения.

 

Геометрические характеристики плоских сечений

Основные понятия

 

Поведение стержня под нагрузкой зависит не только от материала, из которого он изготовлен, но также от очертания его оси, формы и размеров поперечного сечения. Рассмотрим основные геометрические характеристики поперечного сечения элемента.

В координатных осях хоу расположено произвольное поперечное сечение элемента, площадью F (рис. 2.1). В пределах сечения выделяем элементарную площадку dF, координаты центра тяжести которой х, у; ρ - полярная координата.

Основные геометрические характеристики поперечного сечения элемента можно записать так:

(см², м²) – площадь поперечного сечения.

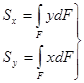(см³, м³) – статические моменты сечения относительно осей х и у.

(см⁴, м⁴) – осевые моменты инерции соответственно относительно осей х и у.

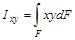(см⁴, м⁴) – центробежный момент инерции.

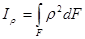(см⁴, м⁴) полярный момент инерции.

I_x, I_y, I_ρ положительны, так текущие координат x, y, ρ входят под интеграл в квадрате.

I_xy может быть положительным или отрицательным, знак зависит от знаков координат х и у, входящих под интеграл.

W_x, W_y (см³) – моменты сопротивления относительно осей х и у.

i_x, i_y (см) – радиусы инерции относительно осей х и у.