Перелік питань
І. Основні закони розподілу випадкової величини
1. Біноміальний розподіл. Його числові характеристики.
2. Геометричний розподіл. Математичне сподівання, дисперсія, середнє квадратичне відхилення.
3. Гіпергеометричний розподіл. Його числові характеристики.
4. Розподіл Пуассона. Математичне сподівання, дисперсія, середнє квадратичне відхилення.
5. Нормальний закон розподілу. Його диференціальна та інтегральна функції, їх властивості та графіки. Числові характеристики. Правило „3-х σ”.
6. Рівномірний закон розподілу. Диференціальна та інтегральна функції. Числові характеристики.
7. Показниковий закони розподілу. Вигляд диференціальної та інтегральної функцій. Числові характеристики.
8. Розподіл 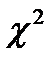 .
.
9. Розподіл Ст’юдента.
10. Розподіл Фішера.
ІІ. Багатовимірні випадкові величини
11. Визначення багатовимірної випадкової величини та її закон розподілу.
12. Система двох дискретних випадкових величин, числові характеристики системи, кореляційний момент, коефіцієнт кореляції.
13. Функція розподілу ймовірностей та щільність ймовірностей системи.
14. Числові характеристики системи двох неперервних випадкових величин.
Дайте відповідь на запитання № ___________________________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____________________
__________
____________________
__________
__________
Практичне заняття 7(Колоквіум)
Елементи дисперсійного та регресійного аналізу
Перелік питань
І.
1. Визначення випадкового процесу та класифікація випадкових процесів. Закони розподілу й основні характеристики.
2. Потік подій та їх властивості.
3. Елементи теорії масового обслуговування (теорія черг).
4. Математична модель для найпростішої системи обслуговування.
ІІ.
5. Модель експерименту. Однофакторний аналіз. Таблиця результатів спостережень.
6. Загальна дисперсія, міжгрупова та внутрішньогрупова дисперсія. Незсуненні оцінки дисперсії.
7. Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій.
ІІІ.
8. Функціональна, статистична і кореляційна залежності.
9. Властивості статистичних оцінок параметрів функції регресії.
10. Вибірковий коефіцієнт кореляції та його властивості.
11. Рівняння парної регресії.
12. Довірчий інтервал для лінії регресії.
13. Коефіцієнт детермінації.
ІV.
14. Множинний коефіцієнт кореляції та його властивості.
15. Нелінійна регресія.
Дайте відповідь на запитання № ___________________________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____________________
__________
____________________
____________________
______________________________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____________________
__________
__________
______________________________
____________________
__________
______________________________
____________________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
____________________
____________________
____________________
____________________
__________
____. _________________________________________________________________
__________
__________
__________
__________
__________
__________
__________
__________
____________________
____________________
____________________
__________
____________________
__________
____________________
__________
__________
__________
__________
__________
__________
__________
__________
Модуль ІІ. МАТЕМАТИЧНА СТАТИСТИКА
Пояснення. Кожна лабораторна робота виконується в аудиторії за допомогою комп’ютера. Результати заносяться до робочого зошиту. По закінченню кожного заняття робочий зошит надається викладачу для перевірки. N – номер студента за списком в журналі.
Лабораторна робота 1
Методи статистичного опису результатів спостережень
План
1. Повторення основних теоретичних положень.
2. Аналітичне та графічне представлення вихідних даних.
3. Знаходження числових характеристик вибіркового розподілу.
4. Підведення підсумків.
Задача 1. Задано вибірку річного надходження податків з розрахунку на один район (тис. грн.):
Необхідно:
1) побудувати інтервальний варіаційний ряд з рівними інтервалами;
2) побудувати для цього варіаційного ряду полігон та гістограму;
3) розрахувати характеристики центру розподілу;
4) обчислити числові характеристики вибіркового розподілу;
5) зробити висновок про однорідність сукупності.
Розв’язання.
1) Для побудови інтервального варіаційного ряду слід визначити кількість груп (К)і величину інтервалу (h) за формулами:
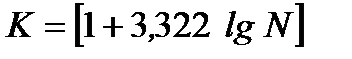 ;
; 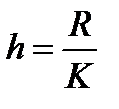 .
.
N 1 – обсяг вибірки. N 1 = N + 20 = _______________________.
R – розмах варіації. 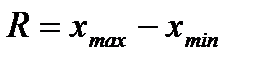 = ______________________.
= ______________________.
Отже,
 ____________;
____________;  = _________.
= _________.
Виходячи з отриманих даних, виконаємо необхідне групування в таблиці.
| № | Границі інтервалів | Середина інтервалу, 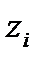
| Частота, 
| Накопичена частота, S, 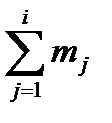
| Відносна частота, 
| Накопичена відносна частота, 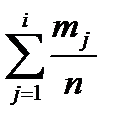
|
| Разом | ― |
2)
3) Знайдемо моду (Мо).
Мода в статистиці – це та варіанта, яка найчастіше повторюється в сукупності.
В інтервальних рядах розподілу мода визначається за формулою:
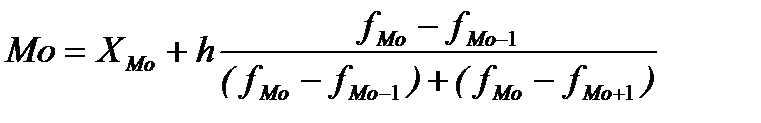 ,
,
де 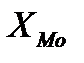 – нижня межа модального інтервалу; h – величина модального інтервалу;
– нижня межа модального інтервалу; h – величина модального інтервалу;  – частота модального інтервалу;
– частота модального інтервалу; 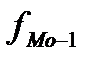 – частота попереднього інтервалу;
– частота попереднього інтервалу; 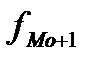 – частота інтервалу, наступного за модальним.
– частота інтервалу, наступного за модальним.
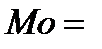 ______________________________________________________
______________________________________________________
Визначимо медіану (Ме).
Медіана – це варіанта, що ділить упорядкований ряд на дві рівні за чисельністю частини. При цьому в одній частині значення варіюючої величини буде меншим, ніж у другій.
В інтервальних рядах розподілу медіана визначається за формулою:
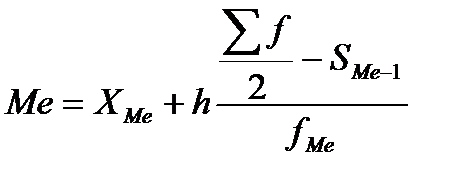
де 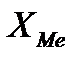 – нижня межа медіанного інтервалу; h — величина медіанного інтервалу;
– нижня межа медіанного інтервалу; h — величина медіанного інтервалу; 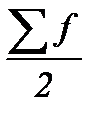 – півсума частот медіанного інтервалу;
– півсума частот медіанного інтервалу; 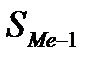 – сума частот перед медіанним інтервалом;
– сума частот перед медіанним інтервалом; 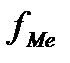 – частота медіанного інтервалу.
– частота медіанного інтервалу.
Підставляючи числові значення, визначаємо:
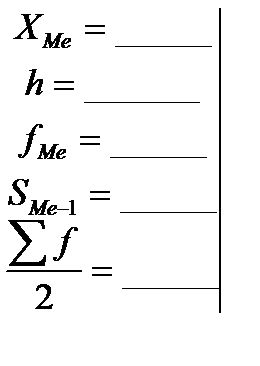
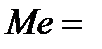 ______________________________________________________
______________________________________________________
4) Знайдемо числові характеристики вибірки за формулами:
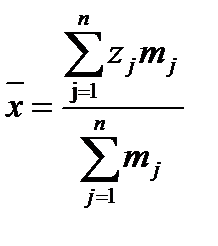 ;
; 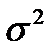
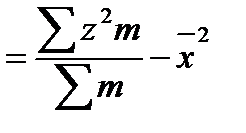 .
.
Допоміжні розрахунки для обчислення характеристик вибірки виконати в таблиці
| № | Границі інтервалів | 
| 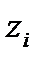
| 
| 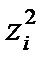
| 
|
| Разом |
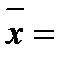 ________________;
________________; 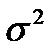
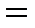 ________________________;
________________________; 
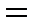 _____________
_____________
5) Для оцінювання однорідності досліджуваної сукупності використовують коефіцієнт варіації 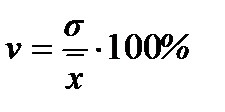 . Сукупність вважають однорідною, а середнє значення – надійним і типовим, якщо коефіцієнт варіації не перевищує 33 %.
. Сукупність вважають однорідною, а середнє значення – надійним і типовим, якщо коефіцієнт варіації не перевищує 33 %.
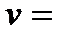 ________________________.
________________________.
Отже, сукупність ___________________________________.
Лабораторна робота 2






