План
1. Повторення формул Бернуллі, Лапласа, Пуассона та випадків їх використання.
2. Розв’язання задач на знаходження ймовірності подій у схемі незалежних повторних випробувань за Формулою Бернуллі.
3. Розв’язання задач на використання потрібної формули в залежності від кількості випробувань.
4. Розв’язання задач на знаходження найімовірнішої частоти та її ймовірності.
Формула Бернуллі: 
,
де n – кількість випробувань Бернуллі, k – число „успіхів”.
Формула локальної теореми Муавра-Лапласа: 
(φ (х) – функція Гаусса; парна; при х > 4 φ(х) = 0; n > 50)
Формула Пуассона: 
(p < 0,1; n > 50 та npq < 9)
Найімовірніша частота: 
Якщо np + p – ціле, то найімовірніша частота має два значення: k 1= np – q та k 2= np + p.
Якщо np + p – дробове, то найімовірніша частота має одне значення: k 0 = [ np + p ].
Формула інтегральної теореми Муавра-Лапласа:
(Φ (х) – функція Лапласа; непарна; при х > 5 Φ(х) = 0,5; n > 50)
Формула для обчислення ймовірності того, що абсолютна величина відхилення випадкової величини від її математичного сподівання не перевищить деякого числа:
.
Формула для обчислення ймовірності того, що абсолютна величина відхилення долі від ймовірності не перевищить деякого числа:
Задача 1. Ймовірність виготовлення на автоматичному верстаті стандартної деталі дорівнює 0,89. Визначити ймовірність того, що з 5 навмання вибраних деталей 3 виявляться стандартними.
Розв’язання.
n = ____________, k = ____________, р = ______________, q = ____________
= __________________________________________________
_______
Відповідь: _____________________________________________________________.
Задача 2. Ймовірність влучення в ціль при одному пострілі дорівнює 0,7. Скласти таблицю розподілу кількості влучень у ціль при 5 пострілах. Побудувати полігон розподілу ймовірностей для отриманого розподілу.
Розв’язання.
n = ____________, р = ______________, q = ____________
k – кількість влучень у ціль
| k | ||||||
| Р |
Задача 3. За статистичними даними в середньому 95% кількості виробів, що виготовляє цех, не мають дефектів. Яка найімовірніша кількість виробів з дефектом виявиться серед 25 випадковим чином відібраних зразків?
Розв’язання.
n = ____________, k = ____________, р = ______________, q = ____________
____________________ 
____________________
Відповідь: _____________________________________________________________.
Задача 4. Банк відправив у свою філію 700 пластикових карток. Імовірність пошкодження чіпа пластикової картки в дорозі дорівнює 0,015. Знайти імовірність того, що при транспортуванні буде ушкоджено 5 пластикових карток.
Розв’язання.
n = ____________, k = ____________, р = ______________
Перевірити виконання умов використання формули Пуассона.
_______
= __________________________________________________
_______
Відповідь: _____________________________________________________________.
Задача 5. Ймовірність появи подій А для кожного окремого випробування дорівнює 0,35. Знайти найімовірніше число появ події А при 70 незалежних повторних випробуваннях та його ймовірність.
Розв’язання.
n = ____________, k = ____________, р = ______________, q = ____________
____________________ ____________________
____________________________________________________
_______
Відповідь: _____________________________________________________________.
Задача 6. У великій партії виробів містяться 62% виробів першого ґатунку. Знайти ймовірність того, що серед 32 випадковим чином відібраних виробів буде 19 першого ґатунку.
Розв’язання.
n = ____________, k = ____________, р = ______________, q = ____________
_____________________________________________________________
_______
Відповідь: _____________________________________________________________.
Задача 7. Школа приймає до перших класів 120 дітей. Визначити ймовірність того, що серед них виявиться 56 хлопчиків, якщо ймовірність народження хлопчика дорівнює 0,517.
Розв’язання.
n = ____________, k = ____________, р = ______________, q = ____________
Перевірити виконання умов використання формули локальної теореми Муавра-Лапласа.
_______
= _______________________________________________
_______
Відповідь: _____________________________________________________________.
Задача 8. Схожість зерна, що зберігається на складі, дорівнює 85%. Вибрали навмання 100 зерен. Потрібно визначити ймовірність того, що серед них:
а) кількість якісних зерен виявиться від 72 до 93 штук включно;
б) кількість якісних зерен буде відрізнятись від найбільш ймовірної кількості їх за абсолютною величиною не більш, ніж на 15 штук;
в) доля (k/n) якісних зерен буде відрізнятись від 0,85 (85%) за абсолютною величиною не більш, ніж на 0,13.
Розв’язання.
n = ____________, р = ______________, q = ____________
а) k 1= ____________, k 2= ____________
= ______________
_______
б)
= ________________________
_______
в)
= ___________________________
_______
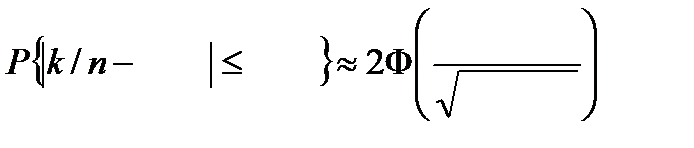Задача 9. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,6. Знайти кількість випробувань n, за якої з ймовірністю 0,7698 можна чекати, що відносна частота (доля) появи події буде знаходитись у межах від 0,58 до 0,62.
Розв’язання.
р = ______________, q = ____________, Р = ___________, n –?
Знайдемо e. _____________________________________________________________
_____________________________________
Відповідь: _____________________________________________________________.
Задача 10. Ймовірність дефекту при виробленні механізмів дорівнює 0,4. Навмання вибирають 500 механізмів. Встановити величину найбільшого відхилення долі виготовлених механізмів з дефектом від ймовірності 0,4, яку можна гарантувати з ймовірністю 0,9973.
Розв’язання.
n = ____________, р = ______________, q = ____________, e –?
_____________________________________
Відповідь: _____________________________________________________________.
