Тема 13. Елементи теорії регресії
Функціональна, статистична і кореляційна залежності. Рівняння праної регресії. Властивості статистичних оцінок параметрів функції регресії. Вибірковий коефіцієнт кореляції та його властивості. Довірчий інтервал для лінії регресії. Коефіцієнт детермінації.
Тема 14. Елементи дисперсійного аналізу
Модель експерименту. Однофакторний аналіз. Таблиця результатів спостережень. Загальна дисперсія, міжгрупова та внутрішньогрупова дисперсія. Незсунені оцінки дисперсії. Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій.
Тема 15. Елементи теорії кореляції
Множинний коефіцієнт кореляції та його властивості. Нелінійна регресія.
Модуль І. ТЕОРІЯ ЙМОВІРНОСТЕЙ
Змістовий модуль 1. Основні поняття і теореми теорії ймовірностей
Практичне заняття 1
Задачі з комбінаторики. Розв’язання задач на класичне означення ймовірності
План.
1. Повторення формул комбінаторики (студенти біля дошки).
2. Розв’язання задач з використанням формул комбінаторики.
3. Повторення класичного означення ймовірності.
4. Розв’язання задач на обчислення ймовірності за класичним означенням з використанням правил комбінаторики.
Формули для обчислення кількості:
Розміщень 
(елементи, порядок)
Поєднань 
(елементи)
Переставлень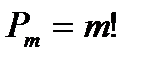 
(порядок)
Основне правило комбінаторики: Всього k дій у певній послідовності можна зробити m 1 × m 2 ×... × mk способами, де mi – кількість способів зробити і -ту дію.
Задача 1. Скільки чотирьохзначних чисел можна скласти з цифр 1, 2, 3, 4, 5?
Розв’язання.
_________________
Відповідь: _____________________________________________________________.
Задача 2. Скільки чотирьохзначних чисел можна скласти з цифр 1, 2, 3, 4, 5, якщо кожну з них можна використовувати не більше одного разу?
Розв’язання.
_________________
Відповідь: _____________________________________________________________.
Задача 3. Скільки є шестизначних чисел, які діляться на 5?
Розв’язання.
_________________
Відповідь: _____________________________________________________________.
Задача 4. Скількома способами можна вибрати делегацію з 30 студентів, яка складається з 5 осіб?
Розв’язання.
___________________________
Відповідь: _____________________________________________________________.
Задача 5. Скільки існує способів розміщення 10 осіб у черзі?
Розв’язання.
___________________________
Відповідь: _____________________________________________________________.
Задача 6. Скільки існує способів впорядкування множини чисел {1, 2, 3, 4,..., n } таким чином, щоб числа 1, 2, 3 знаходились поряд у порядку зростання?
Розв’язання.
___________________________
Відповідь: _____________________________________________________________.
За класичним визначенням
Р (А) = 
,
де m – число подій, якісприяють появі події А, n – загальне число рівноможливих, єдиноможливих та несумісних подій, які можуть з’явитись в результаті даного експерименту.
Задача 7. Кинуто дві гральні кістки. Яка ймовірність того, що сума очок на гранях, які випали, дорівнює 9?
Розв’язання.
А = „сума очок на гранях, які випали, дорівнює 9”
Події, що сприяють події А _______________________________________________
m = ______, n = ________.
________________________________________________________________
Відповідь: _____________________________________________________________.
Задача 8. Яка ймовірність того, що навмання обране число від 1 до 18 буде дільником числа 18?
Розв’язання.
А = „навмання обране число від 1 до 18 буде дільником числа 18”
Події, що сприяють події А _______________________________________________
m = ______, n = ________.
________________________________________________________________
Відповідь: _____________________________________________________________.
Задача 9. При транспортуванні 50 деталей, з яких 6 були браковані, втратилась 1 стандартна деталь. Знайти ймовірність того, що навмання витягнута після цього деталь виявиться стандартною.
Розв’язання.
А = „навмання витягнута деталь виявиться стандартною”
m = ______, n = ________.
________________________________________________________________
Відповідь: _____________________________________________________________.
Задача 10. Абонент забув останні три цифри номера телефону, та, пам’ятаючи, що вони різні, набрав їх навмання. Яка ймовірність того, що він набрав потрібні цифри?
Розв’язання.
А = „абонент набрав потрібні цифри номера телефону”
m = ___________________________________________________________________,
n = ___________________________________________________________________.
________________________________________________________________
Відповідь: _____________________________________________________________.
Задача 11. В урні 9 білих, 6 чорних та 12 червоних куль. Навмання дістають 3 кулі. Яка ймовірність того, що всі вони будуть різного кольору?
Розв’язання.
А = „навмання обрані 3 кулі будуть різного кольору”
m = ___________________________________________________________________,
n = ____.
________________________________________________________________
Відповідь: _____________________________________________________________.
Задача 12. У ліфт дев’ятиповерхового будинку на першому поверсі зайшли 3 особи. Кожна з них з однаковою можливістю може вийти на будь-якому поверсі, починаючи з другого. Знайти ймовірність наступних подій:
А = „всі пасажири вийдуть на четвертому поверсі”;
В = „всі пасажири вийдуть на одному поверсі”;
С = „всі пасажири вийдуть на різних поверхах”.
Розв’язання.
m = ___________________________________________________________________,
n = ___________________________________________________________________.
________________________________________________________________
m = ___________________________________________________________________,
n = ___________________________________________________________________.
________________________________________________________________
m = ___________________________________________________________________,
n = ___________________________________________________________________.
________________________________________________________________
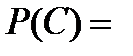Відповідь: _____________________________________________________________.
Задача 13. Є 8 квитків у театр, 5 з яких на місця 1 ряду. Яка ймовірність того, що з 3 навмання обраних квитків 2 виявляться на місця 1 ряду?
Розв’язання.
А = „з 3 навмання обраних квитків 2 виявляться на місця 1 ряду”
m = ___________________________________________________________________,
n = ___________________________________________________________________.
________________________________________________________________
Відповідь: _____________________________________________________________.
Практичне заняття 2
