План
1. Повторення основних теоретичних положень.
2. Розв’язання задач на знаходження ймовірностей, якщо величина розподілена за нормальним законом.
3. Розв’язання задач з використанням нерівності Чебишева та інших наслідків з граничних теорем.
| Диференційна функція розподілу (щільність) |  , а = М(Х)
|
| Інтегральна функція розподілу ВВ Х |  
|
| Ймовірність того, що ВВ Х прийме значення з проміжку [a, b] | 
|
| Ймовірність того, що абсолютна величина відхилення ВВ від її математичного сподівання не перевищить ε | 
|
| Правило „3-х σ” | Будь-яка нормально розподілена ВВ приймає всі свої значення у проміжку (а-3σ; а+3σ) |
| Нерівність Чебишева |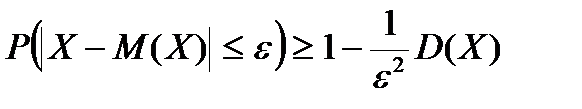 
|
| Для схеми Бернуллі | 
|
| Якщо D(Xі) ≤ C (C>0, і = 1, 2,..., n; Хі попарно незалежні) | 
|
| Зауваження: 1) За умови знаходження нижньої межі величини, що оцінюють, округлення десятинних дробів роблять з нестачею. 2) У випадках, коли про величину p та q нічого невідомо, у правій частині формул (3) та (4) добуток pq вважається рівним 0,25, тобто найбільш можливому значенню. |
Задача 1. Знайти ймовірність того, що нормально розподілена ВВ з математичним сподіванням, яке дорівнює 3, та дисперсією, що дорівнює 4, прийме значення: а) у проміжку [–1;5]; б) не більше 8; в) не менше 5; г) у проміжку (-3; 9).
Розв’язання.
а) Р (–1 ≤ Х ≤ 5) = _________________________________________________________
________
б) Р (– ∞ ≤ Х ≤ 8) = ________________________________________________________
________
в) Р (5 ≤ Х ≤ + ∞) = ________________________________________________________
________
г) Р (– 3 < Х < 9) = ________________________________________________________
________
Задача 2. Випадкова величина Х розподілена за нормальним законом, її математичне сподівання та середнє квадратичне відхилення відповідно дорівнюють 2 та 0,5. Записати диференційну та інтегральну функції розподілу.
Розв’язання.
_______
_______
_______
_______
Задача 3. Випадкова величина Х підкоряється нормальному закону. Математичне сподівання та дисперсія цієї ВВ дорівнюють 6 та 25 відповідно. Знайти ймовірність того, що відхилення ВВ Х від її математичного сподівання за абсолютною величиною не перевищить 2.
Розв’язання.
_______
_______
_______
Задача 4. Випадкова величина Х розподілена нормально з математичним сподіванням а = 10 та середнім квадратичним відхиленням σ = 5. Знайти довірчий інтервал, в який з ймовірністю 0,8664 попадає в результаті випробувань значення випадкової величини Х.
Розв’язання.
= _____________
= _________; 
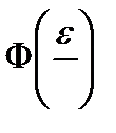= _________; e = _________________________
_______
_______
Задача 5. Нормально розподілена випадкова величина Х має математичне сподівання М (Х) = 2 та дисперсією σ2 = 9. Вкажіть інтервал її практично можливих значень згідно правилу „3-х σ”.
Розв’язання.
_______
_______
Задача 6. Дискретна випадкова величина Х – кількість викликів, що поступають протягом хвилини на комутатор, задана розподілом:
| Х | |||
| Р | 0,1 | 0,2 | 0,7 |
Оцінити ймовірність того, що абсолютна величина відхилення Х від її математичного сподівання не перевищить 1.
Розв’язання.
| Х | Р | Х × Р | Х 2 × Р |
М (Х) = ________; D (X) =___________________________________________________
= ______________________________
Задача 7. Після штампування перевірено 3000 виробів. Серед них виявилося 120 штук з дефектами (брак). Відносна частота (доля) виготовлення бракованих виробів прийнята за приблизне значення статистичної ймовірності виготовлення бракованого виробу. З якою ймовірністю можна гарантувати, що абсолютна погрішність при цьому не буде перевищувати 0,01. Як змінився б результат розв’язку, якщо б така ж відносна частота бракованих виробів була б виявлена при перевірці 30000 виробів? Пояснити причину різних результатів, пов’язуючи цей факт із законом великих чисел.
Розв’язання.
р = ______________, q = ____________
n = ____________
= _________________________________________
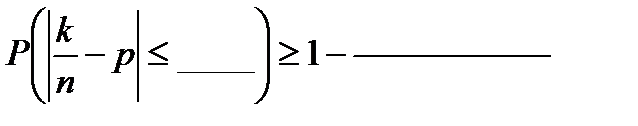n = ____________
= _________________________________________
_______
_______
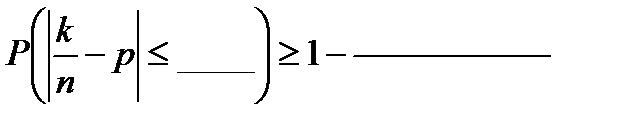Практичне заняття 6(Колоквіум)
