Организ-ые подсис-ы относятся также к обеспечивающим подсис-ам, но в свою очередь на обеспечение эфф-ой работы персонала, и поэтому они могут быть выделены отдельно:
1.Кадровое обеспечение- состав специалистов, участвующих в создании и работе системы, и функциональные обязанности. Состав специалистов может быть следующим:
a) пользователь, формирует проблемы и задачи, подлежащие решению при ведении бизнеса;
b) проблемный программист выбирает прикл-ые прог-ы, к-ые обесп-ют реш-ие деловых задач;
c) системный программист выбирает подходящие ОС, проводит объединение прог-ых ср-тв в единую сис-у, подготовленную для загрузки в нее исходных данных и пакетов прикладных задач.
d) системный интегратор, оценивает сложность задач польз-ля, рекомендует для приобретения аппаратуру и прог-ы, помогает соединять аппаратные модули м-у собой, выбирает и инсталлирует нужные прог-ы, обучает польз-ля и решает вместе с ним заранее опред0ый комплекс реальных задач с применением конкретных данных, настраивая прикладные программы на реальные задачи пользователя.
Эргономическое обеспечение - совокупность методов и средств, используемых при разработке и функционировании ИС, создающих оптимальные условия для деятельности персонала, для быстрейшего освоения системы.
Правовое обеспечение - совокупность правовых норм, регламентирующих создание и функционирование информационной системы, порядок получения, преобразования и использования информации. В состав правового обеспечения входят законы, указы, постановления государственных органов власти, приказы, инструкции и другие нормативные документы министерств, ведомств и местных органов власти.
Организационное обеспечение - совокупность методов и средств. регламентирующих взаимодействие персонала с техническими средствами и между собой в процессе разработки и эксплуатации информационной системы.
Методы расчета оптимальных ОСАУ. Принцип максимума Понтрягина.
Соотношения выполняющиеся на оптимальном процессе, с учётом ограничений в постановке задачи (нет ограничений на состояние, независимость множества допустимых управлений от состояния) позволили определить необходимые условия оптимальности процесса (x*(t), u*(t)).
Полученные соотношения могут быть использованы для “сужения” исходного множества М допустимых процессов путём выделения из него только тех процессов, которые удовлетворяют необходимым условиям.
Совокупность приведённых условий, как правило, даёт возможность выделить единственную траекторию x*(t) из множества допустимых. Если при этом ещё известно (например из содержательной постановки задач) о существовании оптимальной траектории, то тем самым x*(t) и отвечающее ему управление u*(t) и есть решение задачи оптимального управления.
Комплекс условий, которому должен удовлетворять оптимальный процесс, называется принципом максимума Понтрягина. И его можно сформулировать в виде теоремы.
Теорема.
Пусть (x*(t), u*(t)) – оптимальный процесс в задаче оптимального управления (5-7). Тогда существует вектор функция y(t)= (y1(t), y2(t), …, yn(t)), удовлетворяющая вместе с данным процессом следующим условиям:
- Функция
достигает максимума значения по u при x=x*(t), y(t) на значении u=u*(t) при всех tÎ[0;T] (10) - Переменные y(t) удовлетворяют системе дифференциальных уравнений
i=1, 2, …, n,
- В конечный момент времени t=T оптимальная траектория удовлетворяет условиям
i=m+1, m+2, …, n,
где m - переменные
Таким образом, система управлений может быть записана в форме
;
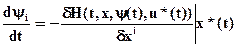i=1, 2, …, n.
