Автоматическим регулятором – называется комплекс устройств, воспринимающий и суммирующий информацию от датчиков и задатчика, формирующий заданный закон регулирования и оказывающий воздействия на объект регулирования, обеспечивающее необходимое качество регулирования.
Классификация регуляторов.
По виду и способу использования энергии для регулирования регуляторы делятся на регуляторы прямого и непрямого действия. Регуляторы непрямого действия по виду потребляемой энергии подразделяются на электрические, пневматические, гидравлические и комбинированные. По виду задающей программы регуляторы подразделяются на регуляторы постоянного параметра, которые поддерживают регулируемую величину на заданном постоянном уровне, программные регуляторы, которые изменяют регулируемую величину по наперед заданной программе, следящие системы.
По характеру изменения регулирующего воздействия во времени различают регуляторы непрерывного и прерывистого действия. Регуляторы прерывистые в свою очередь делятся на релейные, импульсные и цифровые. По структуре регуляторы могут быть приборными и аппаратными.
Для того, чтобы система автоматического была устойчивой и обеспечивала необходимое качество регулирования, регулятор должен обладать определенными динамическими характеристиками, которые могут быть описаны дифференциальными уравнениями, связывающими выходную и входную величины. Эти зависимости носят название законов регулирования, или алгоритмов регулирования. Для выполнения требуемых законов регулирования автоматические регуляторы должны содержать так называемые корректирующие устройства, с помощью которых можно изменять в нужном направлении их динамические характеристики.
Для того, чтобы серийное производство регуляторов стало реальным, все многообразие законов регулирования было сгруппировано по сходным признакам. Унификация законов регулирования позволила осуществить унификацию конструкций регуляторов. Регуляторы каждой группы имеют теперь одни и те же конструктивные элементы и отличаются только положением органов.
Длительный опыт автоматизации ведущих отраслей промышленности убедительно показал, что подавляющее большинство задач по автоматическому регулированию могут быть решены регуляторами со следующими четырьмя линейными унифицированными законами регулирования: пропорциональным, интегральным, пропорционально-интегральным, пропорционально – интегрально - дифференциальным.
П - регуляторы.
П – регуляторы производят перемещение регулирующего органа пропорционально отклонению регулируемой величины от заданного значения.

Коэффициент  называется коэффициентом усиления регулятора.
называется коэффициентом усиления регулятора.
П – регулятор в динамическом отношении подобен безынерционному звену, передаточная функция, АФ и временная характеристики которого определяются формулами:

Для определения АФХ регулятора на его вход подается возмущение синусоидальной формы 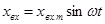 (рис.3.5.) Выходной сигнал регулятора также будет иметь синусоидальную форму
(рис.3.5.) Выходной сигнал регулятора также будет иметь синусоидальную форму  , однако амплитуда и фаза выходного сигнала в общем случае будут зависеть от частоты. Для П – регулятора амплитуда выходного сигнала не зависит от частоты и будет
, однако амплитуда и фаза выходного сигнала в общем случае будут зависеть от частоты. Для П – регулятора амплитуда выходного сигнала не зависит от частоты и будет 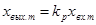 , а фазы входного и выходного сигналов совпадут.
, а фазы входного и выходного сигналов совпадут.
В графической форме АФХ П – регулятора представляет собой отрезок прямой длины  , отложенный по оси абсцисс комплексной плоскости вправо от начала координат (рис.3.6)
, отложенный по оси абсцисс комплексной плоскости вправо от начала координат (рис.3.6)
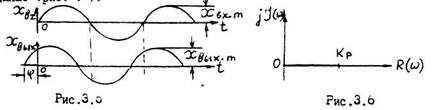
Временная характеристика  или характеристика разгона представляет собой реакцию регулятора на скачкообразное возмущение (рис.3.7).
или характеристика разгона представляет собой реакцию регулятора на скачкообразное возмущение (рис.3.7).
Коэффициент усиления регулятора  является единственным динамическим параметром настройки П – регулятора, т.е. параметром, изменением которого осуществляется настройка регулятора в системе автоматического регулирования по тому или иному критерию на наилучшее качество регулирования.
является единственным динамическим параметром настройки П – регулятора, т.е. параметром, изменением которого осуществляется настройка регулятора в системе автоматического регулирования по тому или иному критерию на наилучшее качество регулирования.
П - регуляторы позволяют устойчиво регулировать работу большинства промышленных регулируемых объектов. Однако они обладают тем недостатком, что при различных нагрузках регулируемого объекта регулируемая величина удерживается регулятором на различных значениях. Объясняется это тем, что перемещение регулирующего органа в новое положение, соответствующее новой нагрузке, может быть произведено только за счет отклонения регулируемой величины. Это явление получило название остаточной неравномерности регулирования или статизма 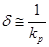

И – регуляторы.
И- регуляторы перемещают регулирующий орган пропорционально интегралу от отклонения регулируемой величины.
 (3.2.)
(3.2.)
Этот закон может быть также записан в следующем виде:

Т.е. И – регуляторы перемещают регулирующий орган со скоростью, пропорциональной отклонению регулируемой величины от ее заданного значения. Иногда интегральные регуляторы называют астатическими, так как в системе регулирования с этими регуляторами отсутствует статическая ошибка. Это определение менее точно ввиду того, что и некоторые другие типы регуляторов обеспечивают в системах отсутствие статической ошибки.
И – регуляторы также как и П – регуляторы имеют один параметр динамической настройки  . Коэффициент
. Коэффициент  носит название приведенной скорости регулирования или скорости разгона. В динамическом отношении И - регулятор подобен интегрирующему звену. Его передаточная функция и АФХ определяются формулами:
носит название приведенной скорости регулирования или скорости разгона. В динамическом отношении И - регулятор подобен интегрирующему звену. Его передаточная функция и АФХ определяются формулами:
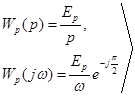 (3.3)
(3.3)
На комплексной плоскости АФХ изображается в виде прямой, совпадающей с отрицательной частью мнимой оси (рис.3.8). Величина угла сдвига фаз интегрального регулятора составляет -900.

Для получения выражения для временной характеристики найдем предварительно изображение регулирующего воздействия при скачкообразном возмущении.

Оригинал этого изображения дает временную характеристику

Если на вход регулятора подается единичное скачкообразное возмущение, то временная характеристика И – регулятора запишется так:

Построим временную характеристику, совместив на одном графике
 . Тогда время интегрирования Ти И - регулятора, являющейся обратной величиной приведенной скорости регулирования
. Тогда время интегрирования Ти И - регулятора, являющейся обратной величиной приведенной скорости регулирования  , можно определить, как время, в течении которого изменение регулирующего воздействия достигнет величины, равной входному скачкообразному воздействию (рис.3.9)
, можно определить, как время, в течении которого изменение регулирующего воздействия достигнет величины, равной входному скачкообразному воздействию (рис.3.9)

ПИ – регуляторы
ПИ – регулятором называют пропорциональный регулятор с введением в закон регулирования интеграла. ПИ - регулятор производит перемещение регулирующего органа
ПИ – регуляторы.
ПИ – регулятором называют пропорциональный регулятор с введением в закон регулирования интеграла. ПИ – регулятор производит перемещение регулирующего органа пропорционально отклонению и интегралу от отклонения регулируемой величины.
Уравнение идеального ПИ – регулятора:
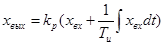 (3.4)
(3.4)
Эта формула может быть представлена также в другом виде:

Т.е. скорость перемещения регулирующего органа пропорциональна отклонению скорости изменения регулируемой величины. ПИ – регуляторы имеют два регулируемых динамических параметра, которые используются в качестве настроечных параметров. Это  -- коэффициент усиления регулятора и
-- коэффициент усиления регулятора и  - постоянная времени интегрирования, величина которой характеризует степень ввода в закон регулирования интеграла. Этот параметр называют иногда временем «изодрома» или временем «удвоения», так как
- постоянная времени интегрирования, величина которой характеризует степень ввода в закон регулирования интеграла. Этот параметр называют иногда временем «изодрома» или временем «удвоения», так как  обычно определяют как время, в течении которого выходная координата
обычно определяют как время, в течении которого выходная координата  регулятора при скачкообразном возмущении достигает своего удвоенного значения (рис.3.9)
регулятора при скачкообразном возмущении достигает своего удвоенного значения (рис.3.9)
В динамическом отношении ПИ – регулятор подобен двум включенным параллельно звеньям: безынерционному с коэффициентом усиления  и интегрирующему со скоростью разгона
и интегрирующему со скоростью разгона 
При беспредельном увеличении времени интегрирования  ПИ - регулятор превращается в пропорциональный. Если устремить
ПИ - регулятор превращается в пропорциональный. Если устремить  и
и  к нулю, но так чтобы их отношение
к нулю, но так чтобы их отношение  оставалось постоянным, то получим интегральный регулятор.
оставалось постоянным, то получим интегральный регулятор.
Передаточную функцию и АФХ идеального ПИ – регулятора легко получить из уравнения (3.4)
 (3.5.)
(3.5.)
На комплексной плоскости АФХ ПИ – регулятора можно изобразить в идее прямой, идущей из бесконечности параллельно мнимой оси (рис.3.10) на расстоянии -  от нее и заканчивающейся на оси абсцисс. ПИ – регулятор занимает промежуточное положение между пропорциональным и интегральным регуляторами. В зависимости от соотношения пропорциональной и интегральной составляющей фазовый угол может изменяться в пределах от 0 до 900.
от нее и заканчивающейся на оси абсцисс. ПИ – регулятор занимает промежуточное положение между пропорциональным и интегральным регуляторами. В зависимости от соотношения пропорциональной и интегральной составляющей фазовый угол может изменяться в пределах от 0 до 900.
Уравнение временной характеристики можно получить с помощью обратного преобразования Лапласа, используя формулу (3.6.) для предаточной функции:
 отсюда
отсюда
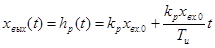 (3.6)
(3.6)
Где  -- скачкообразное возмущение.
-- скачкообразное возмущение.
Построенная по этому уравнению временная характеристика ПИ - регулятора приведена на рис 3.11.
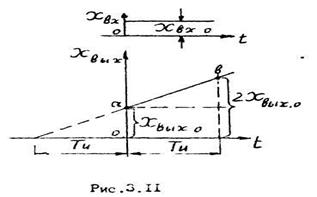
Она состоит из двух частей. Отрезок  характеризует «пропорциональную часть», т.е. изменение регулирующего воздействия в соответствии с первым слагаемым уравнения 3.6. Отрезок ав представляет собой «интегральную часть», которая определяется вторым слагаемым уравнения. Постоянная времени интегрирования
характеризует «пропорциональную часть», т.е. изменение регулирующего воздействия в соответствии с первым слагаемым уравнения 3.6. Отрезок ав представляет собой «интегральную часть», которая определяется вторым слагаемым уравнения. Постоянная времени интегрирования  (рис. 3.11) есть время, в течение которого регулирующее воздействие возрастает на величину, равную пропорциональной части. К этому выводу нетрудно прийти, не прибегая к геометрическим построениям. Достаточно в уравнении (3.6) положить
(рис. 3.11) есть время, в течение которого регулирующее воздействие возрастает на величину, равную пропорциональной части. К этому выводу нетрудно прийти, не прибегая к геометрическим построениям. Достаточно в уравнении (3.6) положить 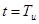 , тогда
, тогда 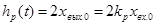
ПИД – регуляторы.
ПИД – регулятором, называется регулятор, производящий перемещение регулирующего органа пропорционально отклонению, интегралу от отклонения и скорости изменения регулируемой величины, т.е. ПИД – регулятор вводит в закон регулирования интеграл и производную от регулируемой величины.
Идеальный ПИД – регулятор описывается следующим уравнением:
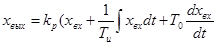 (3.7)
(3.7)
 - постоянная времени диффенцирования или время предварения. Коэффициент усиления
- постоянная времени диффенцирования или время предварения. Коэффициент усиления  , время интегрирования
, время интегрирования  и время диффенцирования
и время диффенцирования  являются тремя динамическими параметрами ПИД – регулятора, используемыми в качестве настроечных параметров.
являются тремя динамическими параметрами ПИД – регулятора, используемыми в качестве настроечных параметров.
Применив к уравнению (3.7) преобразование Лапласа, можно найти передаточную функцию ПИД – регулятора, а также его АФХ (рис.3.12)
 (3.8)
(3.8)

Графически АФХ ПИД – регулятора изображается в виде прямой, параллельной мнимой оси комплексной плоскости, и расположенной на расстоянии  от нее. При
от нее. При  , прямая уходит в
, прямая уходит в  , а при
, а при 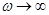 , в
, в  . Фазовый угол ПИД – регулятора может изменяться в пределах от +900 до -900. Получим уравнение временной характеристики:
. Фазовый угол ПИД – регулятора может изменяться в пределах от +900 до -900. Получим уравнение временной характеристики:

Но для скачка  отсюда
отсюда

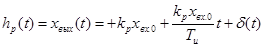
Уравнение временной характеристики идеального ПИД – регулятора состоит из двух частей:

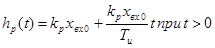 (3.9)
(3.9)
Действительно, в момент действия на вход регулятора скачкообразного сигнала последний член уравнения (3.7) стремится к бесконечности. При t>0, когда входной сигнал сохраняет неизменное значение, член, содержащий производную от отклонения (входного сигнала), равен 0, и переходная функция становится аналогичной функции ПИ – регулятора.


Реальные регуляторы
Применение промышленных регуляторов обычно предполагает, что при работе в реальных условиях эти регуляторы ведут себя как идеальные.
Реальные регуляторы составляются их реальных звеньев. Поэтому передаточные функции реальных регуляторов отличаются от передаточных функций соответствующих идеальных регуляторов. Штейнберг предложил передаточную функцию  реального регулятора представлять в виде произведения передаточной функции
реального регулятора представлять в виде произведения передаточной функции  идеального регулятора и передаточной функции
идеального регулятора и передаточной функции  некоторого звена, которое получило название балластного звена.
некоторого звена, которое получило название балластного звена.
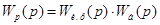 (3.10)
(3.10)
Если регулятор идеальный, то балластное звено 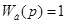 . В случае реального регулятора балластное звено отлично от единицы. Анализ динамики балластного звена позволяет судить об особенностях структурной схемы и настройки того или иного реального регулятора.
. В случае реального регулятора балластное звено отлично от единицы. Анализ динамики балластного звена позволяет судить об особенностях структурной схемы и настройки того или иного реального регулятора.
Степень отличия реального регулятора от идеального для одного и того же прибора может быть различной. Она зависит от величины и формы входного сигнала и от динамических настроек регулятора, т.к. последние влияют на передаточную функцию балластного звена.
Ряд исследований, показали, что если АФХ реального регулятора отличаются от соответствующих характеристик идеального регулятора (в рабочем диапазоне частот) по амплитуде не более чем на 10%, а по фазе не более чем на 15%, то качество регулирования, даваемое реальным регулятором в системе автоматического регулирования, будет незначительно (в допустимой в большинстве случаев степени) отличаться от качества регулирования, даваемого в той же системе идеальным регулятором.
Это условие выполняется не при всех возможных настройках регуляторов при некоторых соотношениях между настроечными параметрами модуль или фаза АФХ реального регулятора могут отличаться от идеального больше, чем на приведенные значения. Это означает, что данный регулятор эксплуатировать в таких режимах нежелательно.
Область настроек динамических параметров реального регулятора, при которых АФХ реального регулятора отличаются от АФХ идеального регулятора, осуществляющего тот же закон регулирования не более чем на 10% по модулю и 15% по фазе, называется областью нормальных режимов регулятора (ОНР).
Совокупность настроек конкретного типа регулятора, которые могут варьироваться при его эксплуатации, зависит не только от границы области нормальных режимов но и от того, в каких пределах может изменяться каждый из настроечных параметров, от расположения границ области устойчивой работы регулятора (при определенных режимах у некоторых типов регуляторов могут возникнуть автоколебания АО внутреннем контуре) и области скользящих режимов. Эту область настроек в отличие от ОПР будем называть областью допустимых настроек (ОПН) регулятора.
ОПН обычно представляется в графической форме (рис.3.15)

ОПН представляет собой область на плоскости динамических настроек ПИ-регулятора, по оси абсцисс которой отложены значения времени интегрирования, а по оси ординат – коэффициент усиления регулятора. Границы ОПН образуются следующими линиями: кривые 3,4,5,6 – определяются крайними положениями ручек настройки динамических параметров  ; кривая 1 является границей области существования скользящего режима; кривая 7 определяется минимальной длительностью управляющих импульсов, которые могут отрабатываться исполнительным механизмом.
; кривая 1 является границей области существования скользящего режима; кривая 7 определяется минимальной длительностью управляющих импульсов, которые могут отрабатываться исполнительным механизмом.
Скользящий режим – основной режим работы релейных регуляторов. В области, где скользящий режим не выполняется, релейные регуляторы работать не могут.
Кривая 2 – определяется частотными характеристиками балластного звена, т.е. вышеупомянутыми условиями близости АФХ реального и идеального регуляторов.
Для ПИД - регуляторов ОНР, а также ОДН будут представлять собой уже не плоскость, а трехмерное пространство ли же набор плоскостей, каждая из которых соответствует определенному значению третьего динамического параметра – времени дифференцирования Io.
Для обеспечения качественной работы автоматических систем регулирования, необходимо следить, чтобы значения динамических параметров регулятора не выходили за пределы заштрихованной области. Если в результате расчета настроек, сделанных для системы, будут получены данные, не находящиеся в нутрии ОДН, то нужно выбрать или другой закон регулирования (например ПИД - закон), либо применить другой регулятор другого типа, имеющий более широкую область допустимых настроек. Если и это не решит задачу, то значит для данного случая необходимо разработать новый уникальный регулятор, обладающий требуемыми характеристиками.
47. функциональные подсистемы информационно -управляющих систем и их характеристики.
Количество обеспечивающих подсистем ни от чего не зависит, а количество функциональных определяется особенностями ПО, а именно: отраслевой принадлежностью, формой собственности, размерами предприятия, характером деятельности предприятия.
Порядок разработки ИС: Цель => ФП => ОП
Для выделения функциональных подсистем существует 4 принципа:
1. Предметный принцип
2. Функциональный
3. Проблемный
4. Смешанный (предметно-функциональный)
С учетом предметного принципа выделяют подсистемы, соответствующие управлению определенными ресурсами (сбыт готовой продукции, управление производством, управление материально-техническим снабжением, управление финансами, управление персоналом и т.п.).
Согласно функциональному принципу выделяют подсистемы, реализующие отдельные функции управления (анализ выполнения планов, финансовый анализ, анализ себестоимости продукции, маркетинговый анализ, планирование производства).
Формирование подсистем по проблемному принципу происходит для гибкого и оперативного принятие решений по отдельным проблемам (ФП класса СППР) (подсистемы бизнес планирования, управления проектами).
На практике как правило чаще всего используется смешанный принцип, согласно которому функциональная структура ИС подразделяется на подсистемы по характеру хозяйственной деятельности. Подсистемы, построенные по функциональному принципу, охватывают обычно все виды хозяйственной деятельности (сбыт, производство, снабжение, персонал, финансы). Подсистемы, которые строятся по предметному принципу, относятся к оперативному управлению ресурсами.
Функциональная подсистема ИС представляет собой комплекс задач с высокой степенью информационных обменов (связей) между задачами. При этом под задачей будем понимать некоторый процесс обработки информации с чётко определенным множеством входной и выходной информации (например, начисление сдельной заработной платы, учёт прихода материалов, оформление заказа на закупку и т.д.).
Состав функциональных подсистем во многом определяется особенностями системы, ее отраслевой принадлежностью, формой собственности, размером, характером деятельности предприятия.
Функциональные подсистемы ИС могут строиться по различным принципам: предметному, функциональному, проблемному, смешанному (предметно-функциональному).
Так, с учетом предметной направленности использования ИС в хозяйственных процессах промышленного предприятия выделяют подсистемы, соответствующие управлению отдельными ресурсами:
• управление сбытом готовой продукции;• управление производством; • управление материально-техническим снабжением; • управление финансами; • управление персоналом.
При этом в подсистемах рассматривается решение задач на всех уровнях управления, обеспечивая интеграцию информационных потоков по вертикали.
Для реализации функций управления выделяют следующие подсистемы:
• планирование;• регулирование (оперативное управление);• учет;• анализ.
48.Виртуальные ресурсы в компьютерных сетях. Виртуальные накопители, виртуальные внешние устройства, виртуальная память и виртуальные процессоры.
Виртуальный — слово, используемое для описания несуществующих предметов, которые выглядят как настоящие.
Под понятием виртуальных ресурсов в компьютере подразумевается аналоги физических устройств, по какой либо причине, отсутствующие явно.
Самый активно используемый виртуальный ресурс в операционной системе – память.
Когда речь заходит о виртуальных процессорах, как правило, имеют в виду процессоры старых марок, которые программно или аппаратно «изображаются», эмулируются на современных процессорах. Так, например, аппаратно реализуется эмуляция процессора 8086 внутри процессоров 80386 и более старших. Еще один, из случаев применения, это кросс-системы, системы, когда на одном типе процессора разрабатывают программы для другого типа процессора (иногда еще не существующего).
Виртуальные сетевые адаптеры, как правило, предназначены для «обмана» операционной системы с тем, чтобы выполнять через них обычные сетевые операции. Примером таких виртуальных сетевых адаптеров являются коммуникационные порты, обычно используемые для управления мышью или модемом.
назначение ВМ виртуального внешнего устройства может быть как постоянным, так и временным. С точки зрения ВМ виртуальное устройство ничем не отличается от реального, оно имеет в ВМ свой физический адрес и ВМ управляет им как реальным устройством.
внешние устройства например, накопители на магнитных лентах.
Виртуальная память - технология, разработанная ради увеличения общего объема памяти, организации множества адресных пространств памяти, их защиты и автоматизации процесса перемещения машинного кода и данных между основной памятью компьютера и вторичным хранилищем.
В настоящее время технология виртуальной памяти имеет аппаратную поддержку на всех современных процессорах.
В случае расположения данных на внешних запоминающих устройствах память может быть представлена отдельным файлом или специальным разделом на жёстком диске.
Также существует термин swap, означающий виртуальную память (точнее способ её представления) или файл подкачки.
Использование технологии виртуальной памяти позволяет:
упростить адресацию памяти клиентским программным обеспечением;
рационально управлять оперативной памятью компьютера (хранить в ней только активно используемые области памяти);
изолировать процессы друг от друга (процесс полагает, что монопольно владеет всей памятью).
Виртуальный процессор является представлением ядра физического процессора в операционной системе логического раздела, использующего общие процессоры.
При установке и запуске операционной системы на сервере без логических разделов, операционная система подсчитывает число операций, которые она может выполнить одновременно, подсчитывая число процессоров сервера. Например, если установить операционную систем на сервер с восемью процессорами, каждый из которых одновременно может выполнять две операции, операционная система сможет выполнить одновременно 16 операций. Точно также при установке операционной систем в логический раздел, использующий выделенные процессоры, операционная система подсчитывает число операций, доступных для выполнения одновременно, пересчитывая число выделенных процессоров, присвоенных данному логическому разделу. В обоих случаях, операционная система легко может вычислить, сколько операций она способна выполнить одновременно, подсчитав число доступных процессоров.
Однако, при установке операционной системы в логическом разделе, использующем общие процессоры, операционная система не может вычислить число операций, основываясь на дробном числе логических процессоров, выделенных данному логическому разделу. В этом случае встроенное ПО сервера должно сообщить об объеме процессорной мощи, доступном операционной системе, как об общем числе процессоров. Это позволяет операционной системе подсчитать число операций, которые она может выполнить одновременно. Виртуальный процессор является представлением физического процессора в операционной системе логического раздела, использующего общие процессоры.
49. Классификация задач оптимального управления:
В общем случае задачу управления нельзя ограничивать только достижением некоторого значения вектора состояния  . Может оказаться, что в таком строгом достижении этого состояния и нет необходимости: важно, чтобы состояние динамической системы не вышло из некоторой области, определяющей многообразие допустимых значений вектора состояния. Естественно, каждому заданному закону управления соответствует закон изменения координат вектора состояния, то есть траектория “движения” управляемого объекта в фазовом пространстве. Зачастую процесс управления осуществляется с “ограниченными ресурсами”, то есть закон управления не может быть произвольным, а должен выбираться из некоторого множества Ω. Математически задача оптимального управления может быть сформулирована так. Дан управляемый динамический объект, вектор состояния которого подчиняется системе уравнений (7.1)
. Может оказаться, что в таком строгом достижении этого состояния и нет необходимости: важно, чтобы состояние динамической системы не вышло из некоторой области, определяющей многообразие допустимых значений вектора состояния. Естественно, каждому заданному закону управления соответствует закон изменения координат вектора состояния, то есть траектория “движения” управляемого объекта в фазовом пространстве. Зачастую процесс управления осуществляется с “ограниченными ресурсами”, то есть закон управления не может быть произвольным, а должен выбираться из некоторого множества Ω. Математически задача оптимального управления может быть сформулирована так. Дан управляемый динамический объект, вектор состояния которого подчиняется системе уравнений (7.1)
Информацию о текущем векторе состояния  x (t) мы получаем из наблюдений
x (t) мы получаем из наблюдений
z = f (x).
Закон управления u (t) определяется с помощью процедуры минимизации функционала вида
Q (x, z, u; t)=min.
Этот функционал и определяет цель управления.
Пусть x (t0) дано. Задача формулируется так, что окрестность x (t1) достигается за некоторый фиксированный отрезок времени T=t1 – t0. Тогда задачу относят к типу задач с фиксированным временем и свободным концом траектории.
Другая постановка. Конец траектории строго фиксирован, то есть x (t1) задано. Требуется найти такое управление и, которое сообщает динамическому объекту траекторию, минимизирующую функционал Q. Время перехода от начального состояния к конечному не фиксировано. Тогда это задача с закрепленными концами фазовой траектории и свободным временем.
В частном случае, взяв в качестве функционала время T, получим задачу на максимальное быстродействие.
Например, задача управления состоит в том, чтобы перевести космический аппарат с одной круговой орбиты на другую, тоже круговую, но более высокую. Такой перевод может быть осуществлен с помощью двух импульсов управления. Если высота новой орбиты задана, то время такого перевода не фиксировано. Имеем задачу со свободным временем и закрепленными концами.
Второй вариант – запуск искусственного спутника Луны. С круговой орбиты около Земли космический аппарат с помощью импульса переводится на орбиту, вытянутую в сторону Луны. По достижении космическим аппаратом окрестности Луны необходимо скорректировать орбиту и превратить ее в круговую около Луны. Эту коррекцию можно выполнить различными способами. Возникает задача: как сэкономить топливо? Здесь концы траектории не закреплены, а ведется поиск закона управления с минимальной энергией, решающего задачу достижения результата за ограниченное допустимое время.
Минимизация функционала – классическая задача вариационного исчисления. В разных прикладных задачах те или иные преимущества имеют:
а) метод динамического программирования Р. Беллмана,
б) метод, основанный на “принципе максимума” Л. Понтрягина.
Последний – более распространен в небесной механике и астродинамике.






