Большинство характеристик реальных устройств в общем случае являются нелинейными и некоторые из них не могут быть линеаризованы, т.к. имеют разрывы второго рода и к ним кусочно-линейная аппроксимация неприменима. Работу реальных звеньев (устройств) могут сопровождать такие явления, как насыщение, гистерезис, люфт, наличие зоны нечувствительности и т.д. Нелинейности могут быть естественными и искусственными (преднамеренно вводимые). Естественные нелинейности присущи системам в силу нелинейного проявления физических процессов и свойств у отдельных устройств. Например, механическая характеристика асинхронного двигателя. Искусственные нелинейности вводятся разработчиками в системы, чтобы обеспечить требуемое качество работы: для оптимальных по быстродействию систем применяют релейное управление, наличие нелинейных законов в поисковых и безпоисковых экстремальных системах, системы с переменной структурой и т.д.
Нелинейной системой называется такая система, в состав которой входит хотя бы один элемент, линеаризация которого невозможна без потери существенных свойств системы управления в целом. Существенными признаками нелинейности являются: если некоторые координаты или их производные по времени входят в уравнение в виде произведений или степени, отличной от первой; если коэффициенты уравнения являются функциями некоторых координат или их производных. При составлении дифференциальных уравнений нелинейных систем сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. Элементы, не допускающие линеаризации, называются существенно нелинейными. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть. В простейшем случае структурная схема САУ нелинейной системы представляет собой последовательное соединение безынерционного нелинейного элемента и линейной части, охваченное обратной связью (рис.7.1). Так как для нелинейных систем не применим принцип суперпозиции, то, проводя структурные преобразования нелинейных систем, единственным ограничением по сравнению со структурными преобразованиями линейных систем, является то, что нельзя переносить нелинейные элементы через линейные и наоборот.
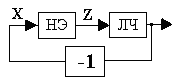
Рис. 7.1. Функциональная схема нелинейной системы:
НЭ - нелинейный элемент; ЛЧ - линейная часть; Z(t) и X(t)
соответственно выход и вход нелинейного элемента.
Классификация нелинейных звеньев возможна по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам. Первые представляются в виде нелинейных статических характеристик, а вторые - в виде нелинейных дифференциальных уравнений. Примеры таких характеристик приведены в [2,6]. На рис.7.2. приведены примеры однозначных (без памяти) и многозначных (с памятью) нелинейных характеристик. В этом случае учитывается направление (знак) скорости сигнала на входе.

Рис.7.2. Статические характеристики нелинейных элементов
Поведение нелинейных систем при наличии существенных нелинейностей имеет ряд особенностей, отличных от поведения линейных САУ [2,6,13 ]:
1. выходная величина нелинейной системы непропорциональна входному воздействию, т.е. параметры нелинейных звеньев зависят от величины входного воздействия;
2. переходные процессы в нелинейных системах зависят от начальных условий (отклонений). В связи с этим, для нелинейных систем введены понятия устойчивости "в малом", "в большом", "в целом". Система устойчива "в малом", если она устойчива при малых (бесконечно малых) начальных отклонениях. Система устойчива "в большом", если она устойчива при больших (конечных по величине) начальных отклонениях. Система устойчива "в целом", если она устойчива при любых больших (неограниченных по величине) начальных отклонениях. На рис.7.3 приведены фазовые траектории систем: устойчивой "в целом" (а) и системы устойчивой "в большом" и неустойчивой "в малом" (б);

Рис.7.3. Фазовые траектории нелинейных систем
3. для нелинейных систем характерен режим незатухающих периодических колебаний с постоянной амплитудой и частотой (автоколебаний), возникающий в системах при отсутствии периодических внешних воздействий;
4. при затухающих колебаниях переходного процесса в нелинейных системах возможно изменение периода колебаний.
Эти особенности обусловили отсутствие общих подходов при анализе и синтезе нелинейных систем. Разработанные методы позволяют решать лишь локальные нелинейные задачи. Все инженерные методы исследования нелинейных систем разделяются на две основные группы: точные и приближенные. К точным методам относится метод А.М.Ляпунова, метод фазовой плоскости, метод точечных преобразований, частотный метод В.М.Попова. Приближенные методы основаны на линеаризации нелинейных уравнений системы с применением гармонической или статистической линеаризации. Границы применимости того или иного метода буду рассмотрены ниже. Следует заметить, что в обозримом будущем имеется необходимость дальнейшего развития теории и практики нелинейных систем.
Мощным и эффективным методом исследования нелинейных систем является моделирование, инструментарием которого служит компьютер. В настоящее время многие сложные для аналитического решения теоретические и практические вопросы сравнительно легко могут быть решены с помощью вычислительной техники.
Основными параметрами, характеризующими работу нелинейных САУ, являются:
1. Наличие или отсутствие автоколебаний. Если автоколебания имеются, то необходимо определить их амплитуду и частоту.
2. Время выхода регулируемого параметра в режим стабилизации (быстродействие).
3. Наличие или отсутствие скользящего режима.
4. Определение особых точек и особых траекторий движения.
Это далеко не полный перечень исследуемых показателей, сопровождающих работу нелинейных систем. Системы экстремальные, самонастраивающиеся, с переменными параметрами требуют оценки и дополнительных свойств.






