В настоящее время широкое применение при синтезе систем автоматики нашёл метод ЛАЧХ (логарифмических амплитудно-частотных характеристик). Этот метод обладает достаточной простотой и наглядностью. Идея метода основана на том, что устанавливается связь между переходным процессом и логарифмической характеристикой, которая выражается в достаточно простом виде. Зная желаемый вид переходного процесса, легко построить соответствующую такому процессу желаемую логарифмическую характеристику. Далее, зная вид желаемой ЛАЧХ, к этому виду приближают исходную ЛАЧХ нескорректированной системы. Это также осуществляется достаточно просто.
Корректирование характеристики имеет свои особенности в зависимости от применяемого вида включения корректирующего устройства, т.е. последовательного или параллельного включения его в основную цепь системы.
Последовательное включение в цепь системы дифференцирующих элементов (опережающих по фазе), позволяет ускорить протекание переходного процесса, а включение интегрирующего элемента (отстающего по фазе) - снизить установившуюся ошибку.
Преимущества последовательной коррекции:
1) относительная простота включения элементов коррекции;
2) расширение полосы пропускания частот при включении дифференцирующего элемента в цепь регулирования.
Недостатки последовательной коррекции:
1) необходимость согласования сопротивлений корректирующих элементов с входным и выходным сопротивлениями элементов системы, к которым подключены вход и выход корректирующего элемента;
2) снижение величины основного сигнала в цепи регулирования, что требует его дополнительного усиления до нужного значения. Отсюда проистекает ограниченность корректируемой системы по мощности.
3) увеличение чувствительности системы к помехам, т.к. расширяется общая полоса пропускания частот,
4) качество работы системы существенно зависит от стабильности характеристик параметров системы,
5) при применении интегрирующих элементов приходится применять конденсаторы относительно большой ёмкости и габаритов,
6) требуются большие входные сигналы постоянного тока.
17. Цифровые регуляторы и выбор периода квантования.
В настоящее время наблюдается тенденция вытеснения аналоговых сис-м управления цифровыми. Объясняется это широкими возможностями по реализации самых совершенных алгоритмов регулирования, что в свою очередь гарантирует получение высокой точности и хорошего быстродействия в замкнутой сис-ме непосредственного цифрового управления.
Цифровой рег-р состоит из АЦП, вычислит.устр-ва и ЦАП.
Схема
: 
Рис.28
В АЦП осущ-ся преобразование непрерывного сигнала ошибки регулир-ия е(t) в числовую послед-ть
Е[кТ] - квантование непрерывного сигнала во времени, а интервал следования чисел
Т – период квантования.
Также происходит округление значения непрерывного сигнала до ближайшей значащей цифры – квантование сигнала по уровню. Шаг квантования по уровню в современ. ВМ прим-ся для управления производствен. процессами и выбирается настолько малым, что и в нормальных режимах работы сис-мы регулирования можно пренебречь.
В вычислит. устр-ве – вычисление текущего значения регулирующего воздействия для каждого шага – преобразование по некоторому з-ну последов-ти чисел ошибки регулир-ия Е[кТ] в послед-ть чисел мю[кТ], к-ая определяет текущее значение регулирующего воздействия.
ЦАП осущ-ет преобразование числовой послед-ти мю[кТ] в непрерывные перемещения регулирующего органа мю(t).
Преобразование воздействий дискретными динамич. сис-ми описыв-ся разностными уравнениями, а не диф.ур-ями.
Линейные разностные ур-ия с постоян.коэф-тами имеют вид:
An*y[(k-n)T]+….+A1*y[(k-1)T]+A0*y(kT)=Bm*x[(k-m)T]+…+B1*x[(k-1)T]+B0*x(kT)
Ai,Bi – постоян.коэф-ты
Методика расчета настроек цифрового регулятора по номограммам
С целью упрощения процедуры настройки цифрового ПИД регулятора рекомендуется согласно Зигрера-Николса выбрать следующие значения отношений.
Тк/Ти=0,2 Тd/Tk=1.25 при Тк=0,1Ткр;
В этом случае коэффициенты d0=2.45; d1=-3.5; d2=1.45
Таким образом в алгоритме настраиваемых параметров остается один коэффициент усиления Кр, чем объясняется простота и распространенность этого метода настроек.
Для цифрового ПИ закона регулирования Тd=0, тогда d0=1,2;
d1= -1; d2=0
После определения периода квантования Тк единственным настраиваем параметрам настраивания параметра является коэффициент усиления цифрового регулятора Кр.Его достаточно просто настроить экспериментально так чтобы декремент затухания в системе был равен 1/4. Однако при известных параметрах объекта управления Кр возможно определить с помощью номограмм, полученных минимизацией критерием по величине Кр.
Методика расчета настроек цифрового регулятора по формулам.
Данный метод предполагает, что переход характера объекта управления, аппроксимированная звеном 1-го порядка с запаздыванием. При этом целью исключения(уменьшения) бросков управляющего сигнала при ступенчатом изменение сигнала задания использования несколько другая форма записи дискретного ПИД -закона регулирования.
u(k)=u(k-1)+Kp[y(k-1)-y(k)+d1[y3-y(k)]+d2(2y(k-1)-y(k-2)-y(k))]
Выбрав период квантования Тк, рассчитывают параметры настройки ПИ или ПИД регулятора по формулам:
Для ПИ: Кр**=(0,9*T)/(тау+Tk/2)-[(0.135*Т*Тк)/((тау+Tk/2)^2)];
d1=(0.27*Т*Тк)/(Kp**(тау+Tk/2)^2);
d2=0 Kp=Kp**/K
Для ПИД:
Кр**=(1,2*T)/(тау+Tk)-[(0.3*Т*Тк)/((тау+Tk/2)^2)];
d1=(0.6*Т*Тк)/(Kp**(тау+Tk/2)^2);
d2=0,5Т/Кр**Тк Kp=Kp**/K
В этих формулах учтено запаздывание Tk/2 на величину свойственное всем замкнутым цифровым системам регулирования.
18. Аппроксимация кривых разгона методом площадей.
В основе метода лежит предположение, что исследуемый объект регулирования может быть описан линейным дифференциальным уравнением с постоянными коэффициентами:
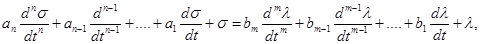
Где 
- постоянные коэффициенты. Передаточная функция объекта, описываемого уравнением (2.18) может быть представлена как
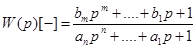(2.19) или в размерной форме
(2.20)
Задача состоит в том, чтобы определить неизвестные коэффициенты , используя для этого систему уравнений (2.21). В Этой системе уравнений 
и для всех значений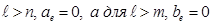 
(2.21)
Входящие в данную систему уравнений коэффициенты 
вычисляются по следующим формулам:
(2.22)
Эти коэффициенты получили название «площадей». Для F1 – это действительно геометрическая площадь (рис. 2.15), а для остальных коэффициентов это название условно. В формулах (2.22) введена новая переменная 
.
В практике чаще всего встречаются следующие объекты:
1. Объекты с самовыравниванием без транспортного запаздывания;
2. Объекты без самовыравнивания и без транспортного запаздывания;
3. Объекты обоих видов, но с транспортным запаздыванием.
