Назначение, классификация и функции СУБД.

К числу функций СУБД принято относить следующие:

Непосредственное управление данными во внешней памяти- функция включает обеспечение необходимых структур внешней памятикак для хранения данных, непосредственно входящих в БД, так и для служебных целей, например, для убыстрения доступа к данным в некоторых случаях (обычно для этого используются индексы).

Управление транзакциями: Транзакция - это последовательность операций над БД, рассматриваемых СУБД как единое целое. Либо транзакция успешно выполняется, и СУБД фиксирует (COMMIT) изменения БД, произведенные этой транзакцией, во внешней памяти, либо ни одно из этих изменений никак не отражается на состоянии БД. Понятие транзакции необходимо для поддержания логической целостности БД.

Журнализация – одно из основных требований к СУБД является надежность хранения данных во внешней памяти. Под надежностью хранения понимается то, что СУБД должна быть в состоянии восстановить последнее согласованное состояние БД после любого аппаратного или программного сбоя. Обычно рассматриваются два возможных вида аппаратных сбоев: так называемые мягкие сбои, которые можно трактовать как внезапную остановку работы компьютера (например, аварийное выключение питания), и жесткие сбои, характеризуемые потерей информации на носителях внешней памяти.

Поддержка языков БД. Для работы с базами данных используются специальныеязыки, в целом называемые языками баз данных. В ранних СУБДподдерживалось несколько специализированных по своим функциям языков. Чаще всего выделялись два языка - язык определения схемы БД(SDL - SchemaDefinitionLanguage) и язык манипулирования данными (DML - DataManipulationLanguage). SDL служил главным образом для определения логической структуры БД, т.е. той структуры БД, какой она представляется пользователям. DML содержал набор операторов манипулирования данными, т.е. операторов, позволяющих заносить данные в БД, удалять, модифицировать или выбирать существующие данные. Классификации СУБД

По модели данных

Примеры: -Иерархические -Сетевые -Реляционные -Объектно-ориентированные -Объектно-реляционные

По степени распределённости

· Локальные СУБД (все части локальной СУБД размещаются на одном компьютере)

· Распределённые СУБД (части СУБД могут размещаться на двух и более компьютерах).

По способу доступа к БД

· Файл-серверные

В файл-серверных СУБД файлы данных располагаются централизованно на файл-сервере. СУБД располагается на каждом клиентском компьютере (рабочей станции). Доступ СУБД к данным осуществляется через локальную сеть. Синхронизация чтений и обновлений осуществляется посредством файловых блокировок. Преимуществом этой архитектуры является низкая нагрузка на процессор файлового сервера. Недостатки: потенциально высокая загрузка локальной сети; затруднённость или невозможность централизованного управления; затруднённость или невозможность обеспечения таких важных характеристик как высокая надёжность, высокая доступность и высокая безопасность. Применяются чаще всего в локальных приложениях, которые используют функции управления БД; в системах с низкой интенсивностью обработки данных и низкими пиковыми нагрузками на БД.

На данный момент файл-серверная технология считается устаревшей, а её использование в крупных информационных системах — недостатком^[2].

Примеры: Microsoft Access, Paradox, dBase, FoxPro, Visual FoxPro.

· Клиент-серверные

Клиент-серверная СУБД располагается на сервере вместе с БД и осуществляет доступ к БД непосредственно, в монопольном режиме. Все клиентские запросы на обработку данных обрабатываются клиент-серверной СУБД централизованно. Недостаток клиент-серверных СУБД состоит в повышенных требованиях к серверу. Достоинства: потенциально более низкая загрузка локальной сети; удобство централизованного управления; удобство обеспечения таких важных характеристик как высокая надёжность, высокая доступность и высокая безопасность.

Примеры: Oracle, Firebird, Interbase, IBM DB2, Informix, MS SQL Server, Sybase Adaptive Server Enterprise, PostgreSQL, MySQL, Caché, ЛИНТЕР.

· Встраиваемые

Встраиваемая СУБД — СУБД, которая может поставляться как составная часть некоторого программного продукта, не требуя процедуры самостоятельной установки. Встраиваемая СУБД предназначена для локального хранения данных своего приложения и не рассчитана на коллективное использование в сети. Физически встраиваемая СУБД чаще всего реализована в виде подключаемой библиотеки. Доступ к данным со стороны приложения может происходить через SQL либо через специальные программные интерфейсы.

Примеры: OpenEdge, SQLite, BerkeleyDB, Firebird Embedded, Microsoft SQL Server Compact, ЛИНТЕР.

7. Оценка качества САР по временным характеристикам.

Любая САР для того, чтобы удовлетворять своему назначению, как уже отмечалось выше, прежде всего должна быть устойчивой. Однако устойчивость является необходимым, но не достаточным условием технической прочности системы регулирования. Помимо устойчивости, к переходному процессу предъявляются требования, обуславливающие его так называемые качественные показатели.

Под качеством системы понимают некоторые свойства кривой ее переходного процесса. Чаще всего рассматривают переходный процесс по управляющему воздействию.

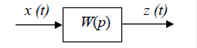
Рис.V.1. Структурная схема САР

Здесь W(p) – передаточная функция САР,

x(t) – входное управляющее воздействие,

z(t) – выходной сигнал.

В качестве управляющего сигнала может быть использован сигнал любого вида, но чаще всего применяется толчкообразный (скачкообразный) сигнал с величиной скачка, равной либо единице, как при получении переходной характеристики системы, либо произвольной величине. Если система обладает колебательными свойствами, то выходной сигнал по управляющему (скачкообразному) сигналу качественно будет выглядеть примерно так, как изображено на рис.V.2.

Из показателей качества (еще говорят: прямых оценок качества регулирования) обычно рассматривают:

1. Установившееся значение выходного сигнала

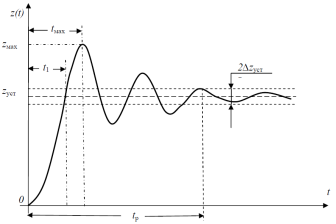
Рис.V. 2. Переходный процесс в САР

2. Точность регулирования Δ – заданная малая постоянная величина, представляющая собой обычно допустимую ошибку. Для входного единичного скачка для технических систем, как правило, Δ = (1÷ 5) %.

3. Время регулирования tр (время переходного процесса).

Выходной сигнал z(t) и его установившееся значение z_уст становятся неразличимы с точностью до величины Δ после времени tp, когда сигнал z(t) войдет последний раз в коридор двойной точности 2Δz_уст и больше никогда из него не выйдет. Таким образом, величина tp определяется как время, протекающее от момента приложения входного скачка до момента, после которого имеет место неравенство:

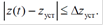
4. Под перерегулированием σ обычно понимают максимальный относительный выброс регулируемого сигнала z(t) = zmax от его установившегося значения zуст, выраженный в процентах

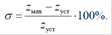
Для большинства промышленных систем σ = (10-40)%.

Здесь были перечислены наиболее часто встречающиеся показатели качества регулирования. Кроме того, для отдельных систем используются и другие показатели, например,

5. Порядок астатизма системы ν.

6. Время tмах наступления максимального значения регулируемой

7. величиныzmax.

8. Время t1 первого пересечения кривой переходного процесса установившегося значения z_уст (характеризует производную z_уст (t)).

9. Количество колебаний переходного процесса за время tp и др.

 

8. Представление импульсного элемента при исследовании импульсных САР.

9. Синтез САР оптимальной по быстродействию.

Функционал имеет вид

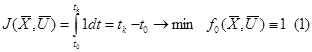
Гамильтонион с учетом (1)

Рассмотрим n-мерный вектор

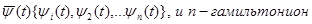
Тогда система уравнений и сопряженная система принимает следующий вид

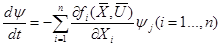
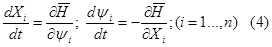
Обозначим верхнюю границу Гамильтониана

Если точная верхняя граница достигается, то это соответствует мах гамильтониана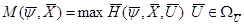

Для рассматриваемого случая

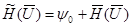т.к. , то

С учетом принятых обозначений, основная теорема ПМ САР оптимальных по быстродействию формулируется следующим образом:

Пусть 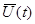при некоторое допустимое управление, переводящее изображение в точку и соответствующее 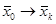, а 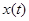-- соответствующее этому управлению траектория. Для оптимальности по быстродействию управления 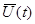и траектории 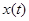необходимо существование такой ненулевой непрерывной векторной функции , удовлетворяющей системе уравнений (4) и что:

1. Для всех 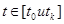функция т.е.

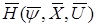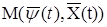= ; (6)

 

2. в конечные моменты времени 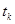выполняется соотношение

Как и в общем случае, если функция 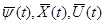удовлетворяют выражению (4) и условию (6), то функция 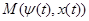постоянна.

Поэтому проверку условия (7) можно производить в любой момент времени на интервале .

Замечание: т.к. для большинства случаев то из выражения и выражения (5) следует, что вдоль оптимальной траектории гамильтониана

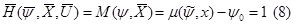
Объект представляет собой 2 последовательности соединенных интегрирующих звена

 

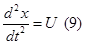
10. Связь между спектрами сигналов на входе и выходе простейшего импульсного элемента(ПИЭ). Теорема Котельникова.

Под ПИЭ понимается такое устройство (гипотетические, не существующие в реальности) выходной сигнал которого представляет собой модулированную последовательность δ-функций, «площади» которых равны дискретным течениям входной величины.

При x(0)=0 спектры сигналов на входе и выходе ПИЭ связаны известным соотношением 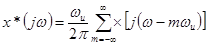, где

x*(jω) – спектр сигнала на выходе ПИЭ,

x(jω) - спектр сигнала на входе ПИЭ,

ω _и – частота квантования сигнала.

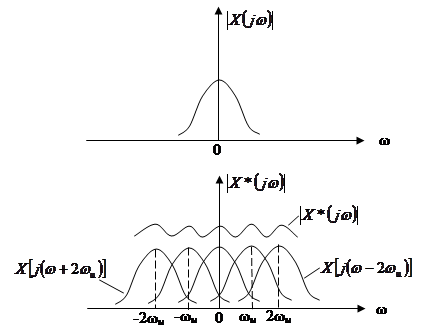Составляющие этого спектрапри m≠0 называются транспонированными составляющими. Сопоставим действительные (можно...) составляющие спектров на входе и выходе ПИЭ. Видно, что сигнал на выходе ПИЭ из-за транспонированных составляющих является периодическим с частотой квантования ω _и, кроме того, ясно, что из спектра выходного сигнала ПИЭ x*(jω), полученного суммированием основной и транспонированных составляющих спектра на входе ПИЭ x(jω), нельзя восстановить спектр входного сигнала, ибо транспонированные составляющие его исказили.

Причина этого понятна – ведь в квантованном выходном сигнале ПИЭ теряется информация о входном сигнале между моментами квантования.

Можно, однако, указать условия, при выполнении которых этой потери информации не происходит:

1) пусть спектр входного сигнала x(t) финитен (конечен) S(jω)=0 при │ω│≥ω_гр;

2) пусть частота квантования сигнала ω_и≥2ω_гр.

Как видно из рисунка, транспонированные составляющие спектра Х*(jω) при ω_и≥2ω_гр не перекрываются с основной составляющей (т.е. m=0), в результате чего в диапазоне частот спектры x(jω) и x*(jω) совпадают (с точностью до пост. множества). Если поставить идеальный фильтр низких частей с постоянным коэффициентом усиления и равномерным пропусканием в полосе , то на его выходе будет получен восстановленный сигнал x(t).

Это все и есть содержание импульсной теоремы Котельникова.

11. Анализ методов решения задач оптимального управления.

Методы оптимизации — поиска экстремума функции при наличии ограничений или без ограничений очень широко используются на практике. Это прежде всего оптимальное проектирование (вы­бор наилучших номинальных технологических режимов, элемен­тов конструкций, структуры технологических цепочек, условий экономической деятельности, повышение доходности и т.д.), оптимальное управление, построение нелинейных математиче­ских моделей объектов управления (минимизации невязок раз­личной структуры модели и реального объекта) и многие другие аспекты решения экономических и социальных проблем (напри­мер, управление запасами, трудовыми ресурсами, транспортны­ми потоками и т.д. и т.п.).

Существует достаточно большое количество численных ме­тодов оптимизации.

Основные из них классифицируются следующим образом:

1. По размерности решаемой задачи: одномерные и многомер­ные.

2. По способу формирования шага многомерные методы де­лятся на следующие виды:

2.1.Градиентные.

· по способу вычисления градиента: с парной пробой и с центральной пробой;

· по алгоритму коррекции шага;

· по алгоритму вычисления новой точки: одношаговые и многошаговые.

2.2. Безградиентные: с поочередным изменением переменных и с одновременным изменением переменных.

2.3. Случайного поиска: с чисто случайной стратегией и со смешанной стратегией.

3. По наличию активных ограничений.

3.1. Без ограничений (безусловные).

3.2. С ограничениями (условные):

· с ограничениями типа равенств;

· с ограничениями типа неравенств;

· смешанные.

 

1. Методы одномерной оптимизации являются базой для не­которых «многомерных» методов. К данному методу относятся

1)метод деления пополам, который основан на делении текущего отрезка [a, b] на две равные части с последующим выбором одной из половин, в которой локализуется максимум в качестве следующего текущего отрезка.

2)метод золотого сечения, который основан на делении текущего отрезка [a, b] на две неравные части, подчиняющиеся правилу золотого сечения. Для определения следующего отрезка, содержащего максимум.

 

2. Многомерная безусловная градиентная оптимизация.

При отыскании экстремумов функции R(x) используются методы без активных ограничений, а величина шага в рекуррентном соотношении x_i+1=x_i+ i вычисляется с использованием градиента целевой функции R(x), т.е. i=f(grad R(x_i)). При этом шаг может определяться с использованием градиента в одной (текущей) или двух (текущей и предыдущей) точках. Направление градиента показывает направление наискорейшего возрастания функции, а его модуль – скорость этого возрастания. К методам данной оптимизации относится метод наискорейшего спуска и метод сопряженных направлений.

 

3. Многомерная безусловная безградиентная оптимизация.

В данных численных методах опти­мизации величина и направление шага к оптимуму формируются однозначно по определенным детерминированным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Все алгоритмы имеют итерационный характер и выражаются формулой
x _i+1 =x _i+f [R(x_i)].

Основная особенность рассматриваемой группы методов — отсутствие вычисления градиента критерия оптимальности. Ряд методов прямого поиска базируется на последовательном применении одномерного поиска по переменным или по другим задаваемым направлениям, что облегчает их алгоритмизацию и применение. К методам данной оптимизации относится метод Зейделя – Гаусса

 

4. Многомерная безусловная случайная оптимизация.

В методах случайного поиска шага при построении улучшающей последовательности x _i+1 =x_i + _i формируется случайным образом. Поэтому в одной и той же ситуации шаг может быть различен в отличие от регулярных методов.

В целом случайные методы поиска предпочтительнее регу­лярных в задачах высокой размерности n>10 и вдали от оптиму­ма. Методы этой группы позволяют в среднем быстрее выходить в район оптимума. Эффективны данные методы и при поиске глобального оптимума. Кроме того, случайные методы имеют ту осо­бенность, что даже при одних и тех же неформально задаваемых параметрах они дадут различные траектории поиска.

 

5. Многомерная условная оптимизация.

К данной оптимизации относятся численные методы по­строения улучшающих последовательностей при наличии огра­ничений типа равенств (связей) и типа неравенств (ограничений). Сюда не входят методы, использующие условия оп­тимальности. Во всех методах строится в допустимой области последовательность точек, в которых значения критерия улучша­ются. Поиск осуществляется градиентным методом.

Допустимая область может формироваться автономными ог­раничениями x_imin x_i x_imax, связями f_j(x₁, x₂, …x_n)=0 (j=1, 2, …m) и ограничениями f_j(x₁, x₂, …x_n)>0, для j = 1,..., р.

Функции, задающие ограничения, могут формировать допус­тимую область с различными свойствами: монотонными, коле­бательными, с большой и малой кривизной и т.д., что оказывает влияние на эффективность методов поиска.

12. Модели управления передачей, обработкой и хранением данных в информационных системах на основе технологии «клиент-сервер»

Как правило, компьютеры и программы, входящие в состав информационной системы, не являются равноправными. Некоторые из них владеют ресурсами (файловая система, процессор, принтер, база данных и т.д.), другие имеют возможность обращаться к этим ресурсам. Компьютер (или программу), управляющий ресурсом, называют сервером этого ресурса (файл-сервер, сервер базы данных, вычислительный сервер...). Клиент и сервер какого-либо ресурса могут находиться, как в рамках одной вычислительной системы, так и на различных компьютерах, связанных сетью.

Основной принцип технологии "клиент-сервер" заключается в разделении функций приложения на три группы:

- ввод и отображение данных (взаимодействие с пользователем);

- прикладные функции, характерные для данной предметной области;

- функции управления ресурсами (файловой системой, базой данных и т.д.)

Поэтому, в любом приложении выделяются следующие компоненты:

- компонент представления данных

- прикладной компонент

- компонент управления ресурсом

Связь между компонентами осуществляется по определенным правилам, которые называют "протокол взаимодействия".

Компанией Gartner Group, специализирующейся в области исследования информационных технологий, предложена следующая классификация двухзвенных моделей взаимодействия клиент-сервер (двухзвенными эти модели называются потому, что три компонента приложения различным образом распределяются между двумя узлами):

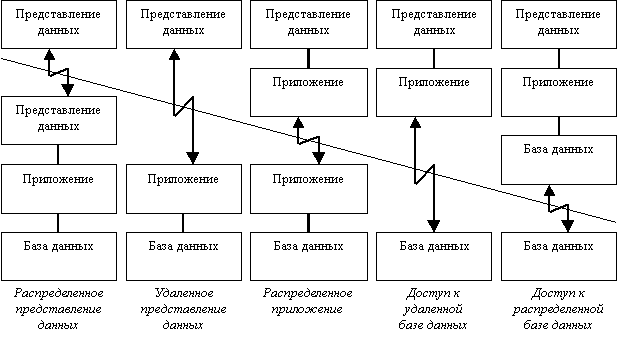
Исторически первой появилась модель распределенного представления данных, которая реализовывалась на универсальной ЭВМ с подключенными к ней неинтеллектуальными терминалами. Управление данными и взаимодействие с пользователем при этом объединялись в одной программе, на терминал передавалась только "картинка", сформированная на центральном компьютере.

Затем, с появлением персональных компьютеров (ПК) и локальных сетей, были реализованы модели доступа к удаленной базе данных. Некоторое время базовой для сетей ПК была архитектура файлового сервера. При этом один из компьютеров является файловым сервером, на клиентах выполняются приложения, в которых совмещены компонент представления и прикладной компонент (СУБД и прикладная программа). Протокол обмена при этом представляет набор низкоуровненых вызовов операций файловой системы. Такая архитектура, реализуемая, как правило, с помощью персональных СУБД, имеет очевидные недостатки - высокий сетевой трафик и отсутствие унифицированного доступа к ресурсам.

С появлением первых специализированных серверов баз данных появилась возможность другой реализации модели доступа к удаленной базе данных. В этом случае ядро СУБД функционирует на сервере, протокол обмена обеспечивается с помощью языка SQL. Такой подход по сравнению с файловым сервером ведет к уменьшению загрузки сети и унификации интерфейса "клиент-сервер". Однако, сетевой трафик остается достаточно высоким, кроме того, по прежнему невозможно удовлетворительное администрирование приложений, поскольку в одной программе совмещаются различные функции.

Позже была разработана концепция активного сервера, который использовал механизм хранимых процедур. Это позволило часть прикладного компонента перенести на сервер (модель распределенного приложения). Процедуры хранятся в словаре базы данных, разделяются между несколькими клиентами и выполняются на том же компьютере, что и SQL-сервер. Преимущества такого подхода: возможно централизованное администрирование прикладных функций, значительно снижается сетевой трафик (т.к. передаются не SQL-запросы, а вызовы хранимых процедур). Недостаток - ограниченность средств разработки хранимых процедур по сравнению с языками общего назначения (C и Pascal).

На практике сейчас обычно используются смешанный подход:

- простейшие прикладные функции выполняются хранимыми процедурами на сервере

- более сложные реализуются на клиенте непосредственно в прикладной программе

На сегодня при создании ИС популярна концепция "тонкого клиента", функцией которого остается только отображение данных (модель удаленного представления данных). Данная концепция базируется на разработке компании MS Active Server Pages (ASP), основной целью которой является создание встроенных в Web-страницы серверных сценариев. Использование данной технологии позволяет использовать в стандартном тексте HTML-страниц фрагменты кода, которые будут выполняться непосредственно на Web-сервере. При этом пользователю будет представляться сформированная на основании приведенных действий ASP Web-страница.

В последнее время также наблюдается тенденция ко все большему использованию модели распределенного приложения. Характерной чертой таких приложений является логическое разделение приложения на две и более частей, каждая из которых может выполняться на отдельном компьютере. Выделенные части приложения взаимодействуют друг с другом, обмениваясь сообщениями в заранее согласованном формате. В этом случае двухзвенная архитектура клиент-сервер становится трехзвенной, а в некоторых случаях, она может включать и больше звеньев.

13. Непрерывно-стохастические модели на примере систем массового обслуживания.

Условно СМО делится на две части:

1) Обслуживаемая система. В ней возникают запросы и обслуживание системы. Она принимает запросы и удовлетворяет их. Схематично можно представить следующим образом.

 

1) Источник – устройство или группа устройств, люди от которых поступает требования в систему обслуживания.

2) Вх. поток требований – это требования поступающие от источника, образуют поток требований или заявок или запросов.

3) Очередь. В тех случаях, когда не м.б. сразу удовлетворены – возникает очередь. Очередь присуща не всякой системе.

4) Обслуживающее устройство – аппарат или канал. Этот элемент создается во всех СМО. От его характеристик зависит время обслуживания требований, длине очереди, время ожидания в очереди.

5) Вых.поток обслуживающих требований – это поток требований выходящих из обслуживающего устройства. Иногда выходной поток из одной системы является вых.потоком из другой системы. Пример: Зрители посмотревшие футбол обслуживаемый стадионом пошли после окончания матча в метро – другой СМО.

Классификация СМО: Выберем признак ожидания выполнения требований. Здесь 4 типа систем:

1) СМО с потерями, отказами (городская телефонная система).

2) Смо с ожиданием (пропускная система в метро)

3) СМО с ограниченной длиной очереди (в магазинах самообслуживания очередь к кассе не м.б. как угодно длинной).

4) СМО с ограниченным временем ожидания (в жизненных ситуациях мы переходим из одной очереди в др.).

Признак количества обслуживающих устройств: одноканальные и многоканальные.

Признак местонахождения источника требований:

1) Если источник поступления требований находится вне СМО, то это разомкнутая система.

2) Если он находится внутри самой системы, то это замкнутая система. Пример: система ремонта и наладки трактора в тракторной бригаде.

В основе СМО лежит понятие потока случайных событий. С потоками связано понятие процесса. 4 класса случайных процессов.