Для процесса возбуждения и генерации колебаний часть их мощности с выхода усилителя (точнее, с колебательной системы) подаётся на его вход по цепи положительной ОС. Говоря другими словами, подобное устройство «возбуждает само себя» и поэтому называется генератором с самовозбуждением.
Механизм возникновения колебаний можно упрощено трактовать следующим образом. При запуске в колебательной системе автогенератора самопроизвольно возникают слабые свободные колебания, обусловленные включением источников питания, замыканием цепей, скачками токов и напряжения в усилительном приборе и т.д. Благодаря специально введённой цепи положительной ОС часть энергий колебаний, возникающих на выходе усилителя, поступает на его вход. Ввиду наличия узкополосной (обязательно высокодобротной) колебательной системы описанные процессы происходят на одной частоте ωр и резко затухают на других частотах.
Вначале, после включения питания автогенератора, усиление сигнала происходит в линейном режиме, а затем, по мере роста амплитуды колебаний, существенную роль начинают играть нелинейные свойства усилительного элемента. В результате амплитуда выходных колебаний генератора, нарастая достигает некоторого установившегося уровня и остаётся практически неизменной. Энергия, отбираемая у источника постоянного тока усилителем схемы за один период колебаний, оказывается равной энергии, расходуемой за то же время в нагрузке. В этом случае говорят о стационарном режиме работы автогенератора.
Автогенератор гармонических колебаний (как, впрочем, и колебаний любой формы и частоты) можно представить обобщенной структурной схемой (рис.5.1), состоящей из нелинейного усилителя с комплексным коэффициентом усиления К =К(jω) и цепи положительной ОС с комплексным коэффициентом передачи по напряжению β =β (jω). В представленной схеме генератора отмечены комплексные амплитуды следующих напряжений: входного – U вх= Uвх(jω); выходного- U вых = Uвых(jω) и обратной связи – U ос = Uос(jω).
Выражение для напряжения ОС на любой частоте генерации ω запишем в виде
U ос = U вх= β U вых (5,1)
тогда выходное напряжение U вых = КU вх, или с учётом (5,1):
U вых = К β U вых (5,2)
Как следует из соотношения (5,2) автогенератор будет работать в стационарном режиме при условии, что
К β = 1 (5.3)
Если же К β > 1, то амплитуда выходных колебаний будет непрерывно нарастать, что определяет необходимое условие самовозбуждения генератора. Представим формулу (5.3) следующим образом:
(5.4)
Здесь К(ω)=К и β(ω)=β – действительные значения коэффициента усиления собственно усилителя (без цепи положительной ОС) и коэффициента передачи положительной ОС; φк(ω)=φк и φβ (ω)=φβ – фазовые сдвиги, вносимые соответственно усилителем ицепью положительной ОС на текущей частоте ω.
В теории автогенераторов выражение (5.4) принято представлять в виде двух равенств:
Кβ=Кос=1 (5.5)
φк+φβ=2πnб (5.6)
где Кос – коэффициент усиления усилителя с ОС; параметр n = 0, 1, 2, 3,….
Соотношение (5.5) определяет условие баланса амплитуд в автогенераторе. Из него следует, что в стационарном режиме на генерируемой частоте коэффициент усиления усилителя с обратной связью Кос равен единице.
Равенство (5.6) характеризует условие баланса фаз. Оно показывает, что в стационарном режиме суммарные фазовые сдвиги сигнала на частоте генерации, создаваемые усилителем и цепью положительной ОС, должны быть равны (или кратны) 2π. Следует отметить, что только условие баланса фаз позволяет определить частоту генерируемых колебаний.
В схемах автогенераторов гармонических колебаний, работающих в стационарном режиме, соотношения (5.5) и (5.6) выполняются на одной фиксированной частоте ωр, которая является резонансной для узкополосной колебательной системы. Наиболее часто в автогенераторах в качестве узкополосных колебательных систем используются резонансные LC-контуры и частотно-зависимые (фазирующие) RC-цепи. Автогенераторы с упомянутыми резонансными контурами называют LC- генераторами, а с фазирующими RC-цепями – RC- генераторами. LC-генераторы способны вырабатывать колебания достаточно высокой частоты (более 100 кГц), RC-генераторы используются для создания гармонических колебаний низкочастотного диапазона (от десятков кГц до единиц и даже долей Гц).
СРОП-4.
LC-генераторы.
Условия самовозбуждения, механизм возникновения гармонических колебаний и зависимость их частоты от параметров схемы рассмотрим на примере LC-генератора на операционном усилителе – ОУ (рис.5.2).
Усилитель генератора охвачен двумя цепями ОС, обеспечивающих режимы балансов амплитуд и фаз. Баланс амплитуд устанавливается цепью отрицательной ОС, содержащий резисторы R1 и R2. С ее помощью задается необходимый коэффициент усиления собственного усилителя |K|=R2/R1. Баланс фаз обеспечивается цепью положительной ОС, состоящей из последовательно включенных резистора R и параллельного колебательного LC- контура. Коэффициент передачи цепи положительной ОС определяется формулой:
Β= 
(5.7)
где R0 – резонансное сопротивление параллельного контура.
Рис. 5.2. Схема LC-генератора на ОУ
На основании первого закона Кирхгофа запишем уравнение токов для неинвертирующего входа ОУ:
iвх+iR+ic+iL=0
Поскольку в идеальном ОУ iвх=0, то
iR+ic+iL=0 (5.8)
Выразим эти токи через соответствующие им напряжения
(5.9)
Введем известное соотношение К=uвых/uвх. Тогда, после дифференцирования по времени и несложных преобразований, уравнение (5.9) примет вид:
Поделив все члены этой формулы на С, запишем:
(5.10)
где ωр = 1/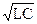 
- резонансная частота контура..
Обозначив эквивалентный коэффициент затухания:
α= 
(5.11)
получим общепринятую в математике форму записи дифференциального уравнения, описывающего колебательный процесс в рассматриваемом автогенераторе:
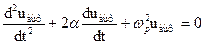(5.12)
Уравнение (5.12) является нелинейным, так как коэффициент усиления К, а, следовательно, и параметр α, зависят от входного напряжения. Как показывает математический анализ, точное решение уравнения (5.12) очень сложно и громоздко, поэтому в теории генераторов используют приближенные методы. Для подобной схемы наиболее простой (с достаточно грубым приближением) способ решения состоит в линеаризации уравнения, и его можно применить для определения условий самовозбуждения генератора. Решение будет точным лишь при малых амплитудах входного напряжения, когда рабочий участок амплитудной характеристики усилителя можно считать линейным.
Полученный результат решения линеаризованного дифференциального уравнения (5.12) описывает гармоническое колебание с экспоненциально изменяющейся амплитудой:
Uвых(t)=U(0)e-αtsinωсвt (5.13)
где U(0) – постоянная, определяемая начальными условиями, а
ωсв= 
(5.14)
- частота свободных колебаний в контуре.
Пример 5.1 Вычислить, насколько частота выходных колебаний автогенератора на ОУ отклоняется от резонансной частоты колебательного контура, если изменения фазы φк=25о. Контур имеет следующие параметры: Q=50, L=160 мкГ, С=160 пФ. Выходное сопротивление ОУ считать равным нулю.
Решение. Известно, что фазовая характеристика параллельного контура вблизи резонансной частоты определяется формулой: φк=-arctg(2Q∆f/fp), где ∆f=f- fp – относительная расстройка. Подставив сюда все заданные значения параметров, находим отклонение частоты:
∆f= fptgφk/(2Q)=4500 Гц = 4,5 кГц.
Характер возникновения и изменения амплитуды выходных колебаний зависит от величины и знак параметра α, и соответственно, от коэффициента усиления К. Рои работе автогенератора возможны три спецефических случая (рис. 5.3):
1. α=0 (К=0). Генерируется выходное гармоническое колебание с постоянной амплитудой и частотой (рис.5.3, а).
2. α<0 (К>1). Возникают выходные колебания, амплитуда которых нарастает по экспоненциальному закону (рис.5.3, б).
3. α>0 (К<1). Амплитуда выходных колебаний генератора затухает по экспоненциальному закону (рис.5.3, в).
Пример 5.2. Задана практическая схема автогенератора на высокочастотном ОУ, работающего в стационарном режиме с циклической частотой выходных колебаний fp=1 МГц. Определить параметры схемы, если значения: Q=50; L=75 мкГ; K=1,1; R1=10 кОм.
Решение. Поскольку в стационарном режиме Кβ=1, и задан К=1,1, то β=0,91. Определим параметры контура: С=1/(4π2 fp2 L)=340пФ; ρ=2πfpL=470 Ом; R0=ρQ=23 кОм. Так как β=R0/(R0+R), то при β=0,91 имеем R=2,6 кОм. Сопротивление резистора R2 цепи отрицательной ОС находим из формулы: R2=|K|·R1=1,1·10=11 кОм.
СРОП-5.
Трехточечные автогенераторы гармонических колебаний
В большинстве схем LС-генераторов напряжения обратной связи снимается с части колебательного контура, т.е используется неполное включение. Поскольку контур при этом имеет три точки соединений, то схемы LС-генераторов (рис.5.6) получили название трехточечных.
Рис.5.6. Схемы трехточечных генераторов:
а – структурная; б – индуктивная трехточка; в – емкостная трехточка.
Упрощенная структурная схема трехточечного автогенератора, построенного на неинвертирующем усилителе представлена на рис. 5.6, а. В схеме реактивные элементы z1, z2 и z3 образуют колебательную систему (резонансный контур), с помощью которой создается частотно-зависимая положительная ОС. В реальных схемах автогенераторов индуктивности и емкости контуров имеют малые омические потери, поэтому при анализе можно учитывать только их реактивные сопротивления х1, х2 и х3.
Предположив, что входное сопротивление усилителя много больше модуля сопротивления элемента z1, находим ток Iвх=Uвых/(z1+ z3). Тогда напряжение ОС
Uос=Uвх=Iвхz1=Uвыхz1/(z1+ z3) (5.15)
и коэффициент передачи петли положительной ОС:
β= 
(5.16)
Так как ОУ в автогенераторе включен по неинвертирующей схеме, то на резонансной частоте, для которой полное реактивное сопротивление контура
х1+х2+х3=0, (5.17)
усилительный каскад не вносит в выходной сигнал фазовый сдвиг и угол φк=0.
Условие баланса фаз (5.6) будет выполняться в том случае, когда и цепь положительной ОС не вносит фазового сдвига (φβ=0). Это возможно обеспечить, если х1 и х3 – реактивные сопротивления одинакового знака, т.е. либо оба элемента – емкости, либо – индуктивности. При таких предположениях для выполнения равенства (5.17) сопротивление х2 должно иметь знак, противополжный знаку сопротивлений х1 и х3. Два варианта построения схем трехточечных генераторов показаны на рис. 5.6, б, в.
Широкое применение в радиотехнике и системах связи находят также автогенераторы, в которых операционные усилители включены по инвертирующей схеме. При этом достаточно в схеме рис. 5.6, б, в поменять местами индуктивность L1 и емкость С1.
Настройку LС-генератора на требуемую частоту осуществляют обычно изменением небольшой емкости дополнительного конденсатора, включенного параллельно основному конденсатору резонансного контура. В современных конденсаторах для изменения частоты колебаний применяют варикапы и подстройку, или даже перестройку частоты, производят с их помощью электронным способом.
СРОП-6.
RC-генераторы.
Технические характеристики LС-генераторов в диапазонах достаточно низких частот существенно ухудшаются из-за резкого возрастания величин индуктивностей и емкостей колебательных контуров и соответствующих им размеров катушек индуктивностей и конденсаторов. Поэтому в низкочастотных автогенераторах в качестве колебательных систем и цепей положительной ОС используют частотно-избирательные RC-цепи. Практически все современные RC-генераторы малой и средней мощностей (до десяти – пятнадцати ватт) строятся на ОУ.
Напряжение положительной обратной связи в RC-генераторах на операционных усилителях можно подавать как на инвертирующий, так и на неинвертирующий входы. В схемах RC-генераторов с неинвертирующим включением частотно-избирательная цепь положительной ОС не должна вносить фазового сдвига в выходной сигнал. В RC-генераторах с инвертирующим включением ОУ, наоборот, RC-цепь положительной обратной связи на частоте генерации должна сдвигать фазу выходных колебаний на угол φβ=π.
Наиболее распространены в радиоэлектронике и технике связи низкочастотные автогенераторы двух видов – с фазосдвигающей RC-цепью и с мостом Вина.
Автогенератор с фазосдвигающей RC-цепью
Такой генератор содержит инвертирующий усилитель и трехзвенную RC-цепь положительной ОС (рис.5.7, а).
Из курса теории цепей известно, что данная трехзвенная RC-цепь (ее называют R-параллель) имеет типовую частотную β(f) и фазовую φβ(f) характеристики, показанные на рис.5.7, б. Анализ графиков частотной и фазовой характеристик показывают, что на квазирезонансной циклической частоте генерации fк трехзвенная RC-цепь положительной ОС имеет вещественное значение коэффициента передачи β=1/29 и вносит фазовый сдвиг φβ=π. Поэтому для обеспечения баланса амплитуд (5.5) необходимо выбирать коэффициент усиления усилителя |K|=R2/R1≥29, а баланс фаз (5.6) обеспечивается автоматически путем инвертирующего включения ОУ.
Можно показать, что квазирезонансная частота генерации для схемы с идеальным ОУ (см.рис.5.7, а) определяется формулой
fk= 
(5.18)
Как следует из этой формулы, частота генерации зависит только от параметров цепи ОС R и C (т.е. внешних элементов усилителя). Если используется четыре RC-звена, то нужен усилитель с К≥18,4, пять RC-звеньев - К≥15,4, шесть - К≥14,1.
Пример 5.3. Для циклической частоты колебаний fk=250 Гц и сопротивления резистора R=25 кОм определить емкость конденсатора с трехзвенной RC-цепью.
Решение. Воспользовавшись формулой (5.18), находим, что необходим конденсатор емкостью С=2,5 мкФ.
Если в схеме рассмотренного RC-генератора поменять местами резисторы и конденсаторы в трехзвенной цепи, то квазирезонансная частота будет определяться соотношением:
fk=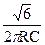 
(5.19)
При этом необходимо обеспечить коэффициент усиления собственно усилителя К≥18,4, поскольку коэффициент передачи такой цепи β≈0,055.
Недостатки RC-генратора на инвертирующем усилителе и трехзвенной RC-цепью – довльно большое количество элементов в петле положительной ОС и, как следствие, трудность перестройки частоты генерации в широком диапазоне. Поэтому чаще применяют автогенераторы с неинвертирующим включением усилителя и мостом Вина в цепи положительной ОС.
СРОП-7.
RC-генератор с мостом Вина.
Данный автогенератор имеет более компактную структуру построения схемы. В ней цепь положительной ОС включается между выходом и неинвертирующим входом ОУ (рис. 5.8, а).
Мост Вина представляет собой частотно-избирательную последовательно-параллельную RC-цепь, состоящую из двух емкостей С и двух сопротивлений R. Частотная β(f) и фазовая φβ(f) характеристики моста Вина (рис. 5.8, б) известны и изучаются в курсе теории цепей. Из графика частотной характеристики следует, что на квазирезонансной частоте генерации коэффициент передачи моста Вина β=1/3. Значит, самовозбуждение автогенератора обеспечивается при коэффициенте усиления усилителя |K|=R2/R1≥3.
Фазовый сдвиг в выходном сигнале отсутствует (φβ=0) только на квазирезонансной частоте (см. рис.5.8, б), которая определяется известной формулой:
fk =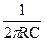 
(5.20)
Перестройка частоты в схеме осуществляется обычно с помощью сдвоенного конденсатора.
Пример 5.4. Частота колебаний в RC-генераторе с мостом Вина fk=500 Гц. Определите параметры схемы, обеспечивающие требуемую частоту.
Решение. Зададим сопротивление моста Вина R=3,9 кОм. Тогда, согласно (5.20) C=1/2πfkR=0,08 мкФ. Так как в автогенераторе |K|=R2/R1≥3, то выбрав сопротивление R2 = 30 кОм, находим R1 = 10 кОм.
СРОП-8.
Стабилизация частоты в автогенераторах
Наиболее важным требованием, предъявляемым к автогенераторам, является высокая стабильность частоты выходных колебаний. Это связан с тем, что во время работы любого автогенератора частота колебаний флюктуирует в некоторых пределах по случайному закону под воздействием различных дестабилизирующих факторов: изменений температуры, влажности и напряжения питания, наличия внешних электромагнитных полей, механических воздействий и пр. Влияние дестабилизирующих факторов проявляется в изменениях величин индуктивностей катушек, емкостей конденсаторов и сопротивлений резисторов, входящих в состав контуров и частотно-избирательных RC-цепей.
В схемах автогенераторов применяют два основных способа стабилизации частоты: параметрический и кварцевый.
