Преобразование сигналов в параметрических цепях

Параметрическими (линейными цепями с переменными параметрами), называются радиотехнические цепи, один или несколько параметров которых изменяются во времени по заданному закону. Предполагается, что изменение (точнее модуляция) какого-либо параметра осуществляется электронным методом с помощью управляющего сигнала. В радиотехнике широко применяются параметрические сопротивления R(t), индуктивности L(t) и емкости C(t).

Примером одного из современных параметрических сопротивлений может служить канал VLG-транзистора, на затвор которого подано управляющее (гетеродинное) переменное напряжение u_г(t). В этом случае крутизна его стоко-затворной характеристики изменяется во времени и связана с управляющим напряжением функциональной зависимостью S(t)=S[u_г(t)]. Если к VLG-транзистору подключить еще и напряжение модулированного сигнала u(t), то его ток определится выражением:

i_c(t)=i(t)=S(t)u(t)=S[u_г(t)]u(t). (5.1)

Как к классу линейных, к параметрическим цепям применим принцип суперпозиции. Действительно, если приложенное к цепи напряжение является суммой двух переменных

u(t)=u₁(t)+u₂(t), (5.2)

то, подставив (5.2) в (5.1), получим выходной ток также в виде суммы двух составляющих

i(t)=S(t)u₁(t)+S(t)u₂(t)= i₁(t)+ i₂(t) (5.3)

Соотношение (5.3) показывает, что отклик параметрической цепи на сумму двух сигналов равен сумме ее откликов на каждый сигнал в отдельности.

 

Преобразование сигналов в цепи с параметрическим сопротивлением. Наиболее широко параметрические сопротивления применяются для преобразования частоты сигналов. Отметим, что термин «преобразование частоты» не совсем корректен, поскольку частота сама по себе неизменна. Очевидно, это понятие возникло из-за неточного перевода английского слова «heterodyning – гетеродинирование». Гетеродинирование – это процесс нелинейного или параметрического смешивания двух сигналов различных частот для получения третьей частоты.

Итак, преобразование частоты – это линейный перенос (смешивание, трансформация, гетеродинирование, или транспонирование) спектра модулированного сигнала (а также любого радиосигнала) из области несущей частоты в область промежуточной частоты (или с одной несущей несущей частоты на другую, в том числе и более высокую) без изменения вида или характера модуляции.

Преобразователь частоты (рис.5.1) состоит из смесителя (СМ) – параметрического элемента (например, МДП-транзистора, варикапа или обычного диода с квадратичной характеристикой), гетеродина (Г) – вспомогательного автогенератора гармонических колебаний с частотой ω_г, служащего для параметрического управления смесителем, и фильтра промежуточной частоты (обычно колебательного контура УПЧ или УВЧ).

Рис.5.1. Структурная схема преобразователя частоты

 

Принцип действия преобразователя частоты рассмотрим на примере переноса спектра однотонального АМ-сигнала. Положим, что под воздействием гетеродинного напряжения

u_г(t)=U_гcos ω_гt (5.4)

крутизна характеристики МДП-транзистора преобразователя частоты изменяется во времени приближенно по закону

S(t)=S_o+S₁cos ω_гt (5.5)

где S_o и S₁ – соответственно среднее значение и первая гармоническая составляющая крутизны характеристики.

При поступлении на МДП-транзистор смесителя АМ-сигнала u_AM(t)= U_н(1+McosΩt)cosω_ot переменная составляющая выходного тока в соответствии с (5.1) и (5.5) будет определяться выражением:

i_c(t)=S(t)u_AM(t)=(S_o+S₁cos ω_гt) U_н(1+McosΩt)cosω_ot=

U_н(1+McosΩt)[S_ocosω_ot+0,5S₁cos(ω_г-ω_o)t+0,5cos(ω_г+ω_o)t] (5.6)

Пусть в качестве промежуточной частоты параметрического преобразователя выбрана

ω_пч=|ω_г-ω_о|. (5.7)

Тогда, выделив ее с помощью контура УПЧ из спектра тока (5.6), получим преобразованный АМ-сигнал с тем же законом модуляции, но существенно меньшей несущей частотой

i_пч(t)=0,5S₁U_н(1+McosΩt)cosω_пчt (5.8)

Заметим, что наличие только двух боковых составляющих спектра тока (5.6) определяется выбором предельно простой кусочно-линейной аппроксимации крутизны характеристики транзистора. В реальных схемах смесителей в спектре тока содержатся также составляющие комбинационных частот

ω_пч=|mω_г±nω_о|, (5.9)

где m и n – любые целые положительные числа.

Соответствующие временные и спектральные диаграммы сигналов с амплитудной модуляцией на входе и выходе преобразователя частоты показаны на рис. 5.2.

 

 

а) б)

 

Рис.5.2. Диаграммы на входе и выходе преобразователя частоты:

а – временные; б – спектральные

 

Преобразователь частоты в аналоговых перемножителях. Современные преобоазователи частоты с параметрическими резистивными цепями построены на принципиально новой основе. В них в качестве смесителей используются аналоговые перемножители. Если на входы аналогового перемножителя подать два гармонических колебания некий модулированный сигнал:

u_с(t)=U_c(t)cosω_ot (5.10)

и опорное напряжение гетеродина u_г(t)=U_гcos ω_гt, то его выходное напряжение будет содержать две составляющие

u_вых(t)=k_au_c(t)u_г(t)=0,5k_aU_c(t)U_г[cos(ω_г-ω_o)t+ cos(ω_г+ω_o)t] (5.11)

Спектральная составляющая с разностной частотой ω_пч=|ω_г±ω_о| выделяется узкополосным фильтром УПЧ и используется в качестве промежуточной частоты преобразованного сигнала.

 

Преобразование частоты в цепи с варикапом. Если на варикап подать только гетеродинное напряжение (5.4), то его емкость приближенно будет изменяться во времени по закону (см.рис. 3.2 в части I):

C(t)=C_o+C₁cosω_гt, (5.12)

где С_о и С₁ – среднее значение и первая гармоническая составляющая емкости варикапа.

Положим, что на варикап воздействуют два сигнала: гетеродинное и (для упрощения расчетов) немодулированное гармоническое напряжение (5.10) с амплитудой U_c. В этом случае заряд на емкости варикапа будет определяться:

q(t)=C(t)u_c(t)=(С_о+С₁cosω_гt)U_ccosω_ot=

=С_оU_c(t)cosω_ot+0,5С₁U_ccos(ω_г - ω_o)t+0,5С₁U_ccos(ω_г + ω_o)t, (5.13)

а ток, протекающий через него,

i(t)=dq/dt=- ω_oС_oU_csinω_ot-0,5(ω_г-ω_o)С₁U_csin(ω_г-ω_o)t-

-0,5(ω_г+ω_o)С₁U_csin(ω_г+ω_o)t (5.14)

Включив последовательно с варикапом колебательный контур, настроенный на промежуточную частоту ω_пч=|ω_г-ω_о|, можно выделить желаемое напряжение.

С реактивным элементом типа варикапа (для сверхвысоких частот это варактор) можно создать также параметрический генератор, усилитель мощности, умножитель частоты. Такая возможность основана на преобразовании энергии в параметрической емкости. Из курса физики известно, что энергия, накопленная в конденсаторе, связана с его емкостью С и зарядом на ней q формулой:

Э= q²/(2С). (5.15)

Пусть заряд остается постоянным, а емкость конденсатора уменьшается. Поскольку энергия обратно пропорциональна величине емкости, то приуменьшении последней энергия растет. Количественное соотношение такой связи получим, дифференцируя (5.15) по параметру С:

dЭ/dC= q²/2C²=-Э/С (5.16)

Это выражение также справедливо и для малых приращений емкости ∆С и энергии ∆Э, поэтому можно записать

∆Э=-Э (5.17)

Знак минус здесь показывает, что уменьшение емкости конденсатора (∆С<0) вызывает увеличение запасаемой в нем энергии (∆Э>0). Увеличение энергии происходит за счет внешних затрат на выполнение работы против сил электрического поля при уменьшении емкости (например, путем изменения напряжения смещения на варикапе).

При одновременном воздействии на параметрическую емкость (или индуктивность) нескольких источников сигналов с разными частотами, между ними будет происходить перераспределение (обмен) энергий колебаний. На практике энергия колебаний внешнего источника, называемого генератором накачки, через параметрический элемент передается в цепь полезного сигнала.

Для анализа энергетических соотношений в многоконтурных цепях с варикапом обратимся к обобщенной схеме (рис.5.3). В ней параллельно параметрической емкости С включены три цепи, две из которых содержат источники e₁(t) и e₂(t), создающие гармонические колебания с частотами ω₁ и ω₂. Источники соединены через узкополосные фильтры Ф₁ и Ф₂, пропускающие соответственно колебания с частотами ω₁ и ω₂. Третья цепь содержит сопротивление нагрузки R_н и узкополосный фильтр Ф₃, так называемый холостой контур, настроенный на заданную комбинационную частоту

ω₃ = mω₁+nω_2, (5.18)

где m и n – целые числа.

Для упрощения будем считать, что в схеме применены фильтры без омических потерь. Если в схеме источники e₁(t) и e₂(t) отдают мощности Р₁ и Р₂, то сопротивление нагрузки R_н потребляет мощность Р_н. Для замкнутой системы в соответствии с законом сохранения энергии получим условие баланса мощностей:

 

Р₁+Р₂+Р_н=0 (5.19)

 

 

Рис. 5.3. Обобщенная схема с параметрической емкостью

 

Умножив и разделив здесь каждое слагаемое на соответствующую частоту, получим:

(5.20)

Запишем это уравнение в другом виде

ω₁ +ω₂ 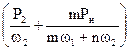=0 (5.21)

Полученное равенство должно быть тождественным при любых частотах. Это, очевидно, возможно, если

=0; 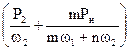=0. (5.22)

Эти два фундаментальных соотношения называют уравнениями Мэнли-Роу. Они позволяют просто и наглядно выяснить закономерность преобразование мощностей сигнала и накачки в многоконтурных параметрических цепях. Рассмотрим наиболее распространенный случай, имеющий место в параметрических цепях устройств радиоэлектроники.

 

Параметрическое усиление с преобразованием частоты. Пусть в параметрической схеме, структурно показанной на рис.5.3. e₁(t) – источник усиливаемого сигнала, а e₂(t) – генератор накачки. Положив в формулах (5.22) значение коэффициентов m=n=1, получим

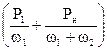=0; =0 (5.23)

Будем считать (как это принято в физике) мощность, выделяемую на активной нагрузке, положительной, а мощность, отдаваемую генератором, отрицательной. Тогда их (5.23) следует, что при Р_н>0 мощности Р₁<0 и Р₂<0. Значит, при настройке холостого контура на частоту ω₃=ω₁+ω₂ источник усиливаемого сигнала и генератор накачки будут отдавать мощность в нагрузку, и схема превращается в параметрический усилитель входного сигнала. При этом усиление сигнала сопровождается повышением его частоты.

С помощью параметрической цепи возможно также усиление мощности входного сигнала с понижением его частоты. Нетрудно показать, что это будет иметь место в данной схеме при настройке холостого контура на разностную частоту ω₃=ω₁-ω₂ и выборе m=1, n =-1 в формуле (5.22).