Выше было сказано, что нелинейные цепи могут преобразовывать спектры колебаний: сместить на частотной оси, образовать новые частотные компоненты. Это свойство нелинейных цепей используется во многих радиотехнических устройствах, таких как умножители и преобразователи частоты, модуляторы, детекторы. Перечисленные устройства, объединенные общим названием «преобразователи спектра», выполняют по одинаковой структурной схеме, содержащей нелинейный или параметрический элемент – преобразователь X/Y и фильтр FF. Преобразователь искажает форму подаваемых колебаний и таким образом создает высшие гармоники и колебания с комбинационными частотами, фильтр выделяет нужные из них.
В качестве нелинейного элемента в преобразователях спектра применяют диоды, транзисторы, элементы с нелинейной емкостью, а также составные функциональные узлы, распространенным примером которых является перемножитель напряжений.
Аналоговым перемножителем напряжений называют интегральные микросхемы, предназначенные для выполнения операции перемножения двух сигналов и выдачи результата перемножения в форме напряжения
Uвых=UxUy/Ur=KпUxUy (6.1)
где Ur=Kп-1 – масштабирующее напряжения.
Особенностью операции перемножения является то, что полярность выходного напряжения определяется полярностями двух входных напряжений, каждое из которых может быть как положительным, так и отрицательным. Если входные и выходные сигналы могут быть как положительными, так и отрицательными, и полярности их согласованы, то такой перемножитель называется четырехквадрантным. Графическая зависимость выходного напряжения от входных напряжений Ux и Uy приведена на рис. 6.1. Если входной сигнал изменяет полярность при изменении полярности только одного входного сигнала, то умножитель называют двухквадрантным. Если все сигналы могут быть только однополярными, то умножитель называют одноквадрантным.
Рис.6.1. Передаточные характеристики перемножителя напряжений.
Масштабирующее напряжение Ur обычно является постоянным (хотя и с подстройкой), но в большинстве микросхем перемножителей значением этого напряжения можно управлять, подавая ток или напряжение управления на третий вход. Для получения высокой точности перемножения сигналов в микросхемах вводятся по крайне мере четыре регулировки, позволяющие установить требуемый коэффициент передачи Кп и устранить прямое прохождение сигналв Uх и Uу. Кроме этого, вводится регулировка смещения нулевого уровня. Масштабирующий коэффициент выбирают в пределах 1/25 ÷10. Но в большинстве случаев масштабирующий коэффициент перемножителя выбирают таким, чтобы выполнялось соотношение
Uвых= UxUy/10 (6.2)
т.е. Кп=0,1 В-1. Это условие использовано при построении графика рис. 6.1.
Разработано несколько способов построения аналоговых перемножителей: логарифмирующие, квадратирующие, с широтноимпульсной модуляцией и др., однако в интегральных микросхемах преимущественно применяется метод построения перемножителей на принципе переменной крутизны. Базовая схема перемножителя с переменной крутизной приведена на рис 6.2, а, а его упрощенная структурная схема изображена на рис.6.2, б.
Метод переменной крутизны основан на зависимости крутизны биполярного транзистора от тока эмиттера. С этой целью в схему введен дифференциальный каскад, на вход которого подается сигнал Ux. Выходное напряжение дифференциального каскада пропорционально произведению крутизны S на входное напряжение Ux:
Uвых=SRнUx (6.3)
где Rн – сопротивление нагрузки.
Рис.6.2. Упрощенная схема перемножителя с переменной крутизной:
Принципиальная (а) и структурная (б)
Для регулирования крутизны дифференциального каскада в схему введен преобразователь напряжения Uy в ток іэ на транзисторе Т3. При достаточно большом значении сопротивления Rэ ток эмиттера транзистора Т3 можно определить по формуле
іэ = Uy/ Rэ
В свою очередь, крутизна биполярного транзистора, используемого в дифференциальном каскаде, определяется из уравнения Эберса-Молла
Ik=Is 
(6.4)
При выполнении условия Uбэ>φT ток коллектора 
, откуда находим крутизну транзистора в виде
S= 
= 
∙ 
. (6.5)
Подставляя значения крутизны и ток эмиттера, найдем выходное напряжение:
Uвых= RyUx= 
UxUy=КпUxUy (6.6)
где Кп=Rн/(RэφТ) – коэффициент передачи перемножителя.
Приведенная базовая схема перемножителя имеет ряд существенных недостатков:
· Входной дифференциальный каскад имеет симметричный выход, не позволяющий применять заземленную нагрузку:
· Преобразователь напряжения Uy в ток іэ имеет несимметричный вход и, следовательно, на вход Uy можно подавать сигнал только одной полярности, т.е. преобразователь может быть только двухквадрантным;
· Входной сигнал Ux связан с коллекторным током и напряжением эмиттерного перехода экспоненциальной зависимостью (6.4), которая вносит нелинейность, даже при очень малом уровне напряжения Ux.
Для устранения этих недостатков схему перемножителя усложняют. Для создания симметричного входа по сигналу Uy базовую схему дополняют вторым дифференциальным каскадом, входы которого включены параллельно входам первого. Коллекторные выходы второго каскада соединены перекрестно с коллекторными выходами первого каскада, как показано на рис.6.3. Благодаря симметричному входу сигнала Uy усовершенствованный перемножитель может работать вовсех четырех квадрантах, т.е. становится четырехквадрантным.
а) б)
Рис.6.3. Упрощенная схема четырехквадрантного перемножителя (а) и преобразователь симметричного выходного сигнала в несимметричный (б)
Для схемы этого перемножителя можно записать уравнение, определяющее выходное напряжение:
uвых=Rн(i1+i3)-Rн(i2+i4) (6.7)
Если оба входных напряжения равны нулю, т.е. uх= uу=0, то все токи одинаковы: i1=i2+ i3=i4= iо. В этом случае выходное напряжение uвых также равно нулю. Если же, например uу=0, а uх>0, то токи i1 и i2 увеличатся, а i3 и i4 уменьшатся. При малом uх связи между токами и напряжениями можно представить в виде:
i1 = i2 = iо(1+кхuх); i3 = i4 = iо(1-кхuх), (6.8)
где кх – коэффициент пропорциональности. Подставив (6.8) в (6.7) получим, что и в этом случае uвых=0.
При uх=0 и uу>0, приняв, что
i1 = i4 = iо(1+куuу), i2 = i3 = iо(1-кхuх), (6.9)
также получим uвых=0.
Наконец, если оба напряжения не равны нулю, то по аналогии с (6.8) и (6.9), записав
i1 = iо(1+кхuх)(1+куuу);
i2 = iо(1+кхuх)(1-куuу);
(6.10)
i3 = iо(1-кхuх)(1-куuу);
i4 = iо(1-кхuх)(1+куuу)
и подставив (6.10) в (6.7), найдем
uвых=4kxkyRнiouxuy=kпuxuy (6.11)
где kп=4kxkyRнio – коэффициент пропорциональности.
Преобразование симметричного выхода перемножителя в несимметричный в специализированных микросхемах выполняют при помощи дифференцмального усилителя на ОУ. Схема подключения такого усилителя приведена на рис.6.3, б. Коэффициент передачи такого усилителя равен отношению Ro/R1.
Применение перемножителей. Как уже отмечалос, микросхемы перемножителей находят применгение в различных электронных устройствах. Кроме того, они входят составной частью во многие специализированные микросхемы и узлы. Столь широкое применение ИМС перемножителей обусловлено прежде всего тем, что нелинейная операция перемножения приводит к изменению спектра выходного сигнала. Так, например, если оба сигнала Uх и Uy гармонические, но с разной частотой ωх и ωу, то
Uх= Umxcos(ωxt), Uy= Umycos(ωyt) (6.12)
В результате перемножения этих сигналов на выходе перемножителя образуются два сигнала, один из которых имеет суммарную, а другой – разностную частоту
Uвых(t)=0,5KпUmxUmy[cos(ωx-ωy)+ cos(ωx+ωy)] (6.13)
Амплитуды сигналов одинаковы и равны 0,5KпUmxUmy. В то же время на выходе перемножителя отсутствуют сигналы с частотами перемножаемых сигналов. Такое преобразование двух сигналов является операцией балансной модуляции. Если же на оба входа перемножителя подать один и тот же сигнал Ux= Uy=Umcosωt, то выходное напряжение будет содержать постоянную составляющую и сигнал удвоенной частоты
Uвых(t)=0,5KпUm2(1+cos2ωt) (6.14)
Если отфильтровать постоянную составляющую, то получится схема удвоения частоты.
Квадратор. Если в формуле (6.14) с помощью конденсатора отфильтровать переменную составляющую, то получим величину пропорциональную квадрату входного напряжения:
, т.е. Uвых=КUxUy=КUx2, (при Ux=Uy).
(6.15)
Рис.6.4. Квадратор.
Аналоговые делители. Как известно, деление – действие обратное умножению.
Рис.6.5. Схема деления на ОУ.
Здесь U1 – одно из входных напряжений, которое надо поделить на второе входное напряжение Uх.
Из приведенного рисунка видно, что U2=KUxUy, но с другой стороны U2=KUxUвых. Далее ток I1=U1/R; ток I2=U2/R. Но эти токи по модулю равны друг другу, как и в любой схеме на ОУ (из-за ее большого входного сопротивления). Т.е. I1=I2, следовательно U1=U2 или U1= KUxUвых, отсюда следует, что
Uвых= 
(6.16)
Извлечение квадратного корня. Извлечение квадратного корня является обратной операцией возведения в квадрат. Поэтому, чтобы произвести операцию извлечения, необходимо в обратную связь схемы на рис. 6.6. поместить квадратор. Из рисунка следует: U2=KUвых2, но Uвх =U1=U2 (как показано было выше).
Значит: Uвых= 
(6.17)
Рис.6.6. Схема извлечения квадратного корня.
Кроме этих применений, перемножители можно использовать для вычисления активной и реактивной мощности, определения фазового сдвига двух напряжений, деления частоты сигналов и во многих других случаях.
СРОП-1.
Спектр периодических сигналов
Очень часто математическое описание даже несложных по структуре детерминированных сигналов является весьма трудной задачей. Поэтому в теории электрических цепей и радиоэлектронике используется прием, при котором реальные сигналы заменяют (аппроксимируют, представляют, декомпозируют) набором идеализированных математических моделей, описываемых простыми функциями. Это дает важный инструмент для анализа прохождения сигналов через радиотехнические цепи. Подобным образом можно также упростить задачу синтеза сложных сигналов из совокупности простых сигналов.
Согласно теореме Фурье любое изменение во времени некоторой функции можно представить (аппроксимировать) в конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Представим периодический сигнал наиболее распространенной тригонометрической формой ряда Фурье:
u(t)=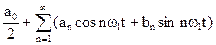 
. (1.1)
Здесь а0=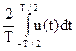 
-постоянная составляющая (1.2)
аn = 
- косинусоидальные составлющие
bn =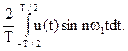 
- синусоидальные составлющие (1.4)
Спектральную составляющую с частотой ω1 в радиотехнике называют первой (основной) гармоникой, а составляющие с частотами nω1 (n>1) – высшими гармониками периодического сигнала.
Из курса математики известно, что если сигнал представляет собой четную функцию времени u(t)=u(-t), то в тригонометрической записи ряда Фурье (1.1) отсутствуют синусоидальные коэффициенты bn, так как в соответствии с формулой (1.4) они обращаются в нуль. Для сигнала u(t), определяемого нечетной функцией времени, наоборот, нулю равны косинусоидальные коэффициенты an, ряд содержит составляющие bn.
С математической точки зрения часто удобнее выражение (1.1), описывающее заданный сигнал, представить в другой, эквивалентной форме ряда Фурье: u(t)= A0+ 
(1.5)
где А0=а0/2, Аn=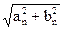 
- амплитуда, а φn=arctg(bn/an) – начальная фаза n-й гармоники сигнала.
В радиоэлектронике и теории сигналов также широко используется комплексный ряд Фурье
u(t)= 
, (1.6)
где Cn=Cn(jω)= 
(1.7)
- комплексная амплитуда n–й гармоники.
Наиболее наглядно о спектре радиотехнического сигнала можно судить по его графическому изображению – спектральной диаграмме. В теории сигналов различают амплитудно-частотные и фазо-частотные спектры. Совокупность амплитуд гармонических составляющих An носит название спектра амплитуд, φn – спектра фаз. Cn – комплексного спектра (см. рис.1).
Рис.1. Спектры периодического сигнала: а – амплитудный; б – фазовый;
в - комплексный.
Спектр периодического сигнала принято называть линейчатым или дискретным, так как он состоит из отдельных линий, высота которых равна амплитуде Аn соответствующих гармоник. Из всех видов спектров наиболее информативен амплитудный, поскольку с его помощью можно оценить количественное содержание тех или иных гармоник в частотном составе анализируемого сигнала. В теории сигнала доказано, что амплитудный спектр является четной функцией частоты, а фазовый - нечетной.
Если используется четыре RC-звена, то нужен усилитель с К≥18,4, пять RC-звеньев - К≥15,4, шесть - К≥14,1.
СРОП-2.
Спектральное представление непериодических сигналов.
В теории спектрального представления непериодических (импульсных) сигналов используется искусственный прием, формально заменяя такие сигналы периодическими с бесконечно большим интервалом (периодом) следования Т→∞.
Положим, что некоторая заданная функция u(t) аналитически описывает одиночный импульсный (иногда называемый финитным) сигналом конечной длительности(рис.2.12, а). Мысленно дополнив его такими же импульсными сигналами, следующим с некоторым интервалом Т (рис.2.12, б) получим периодическую последовательность аналогичных импульсов un(t)=u(t+nT). Для того чтобы вне искусственно введенного интервала 0, Т исходный сигнал был равен нулю, необходимо увеличить период повторения импуль-
СРОП-3.
Генераторы гармонических колебаний
Устройства, предназначенные для создания электрических колебаний, называют генераторами. С точки зрения режима работы их разделяют на автогенераторы и генераторы с внешним возбуждением.
Автогенератор – устройство, преобразующее энергию постоянного тока в энергию электрических колебаний требуемой частоты и формы.
Генератор с внешним возбуждением (в импульсной технике – ждущий генератор) переходит в режим генерации, формирования, или усиления электрических колебаний только при поступлении на его вход сигналов возбуждения (запуска).
В зависимости от формы вырабатываемых напряжений различают генераторы гармонических и релаксационных (импульсных) колебаний. Генератор гармонических колебаний вырабатывает сигнал, в спектре которого присутствует практически одна гармоника. Выходные колебания релаксационного генератора содержит широкий спектр гармонических составляющих, часто имеющих соизмеримые амплитуды. Можно отметить и генераторы линейных пилообразных напряжений, которые относятся к релаксационным. Особую группу представляют автогенераторы случайных колебаний – шумовые генераторы. Независимо от назначения, принципа действия и схемотехнического выполнения а в т о г н е р а т о р любых перечисленных колебаний (кроме параметрических схем) состоит из нелинейного усилителя, цепи положительной обратной связи (ОС) и источника питания постоянного тока. Форма и частота выходных колебаний определяется только параметрами самого автогенератора, между тем как в генераторе с внешним возбуждением амплитуда и частота колебаний навязывается из вне.
Генератор гармонических колебаний должен обязательно содержать узкополосную колебательную систему. Принцип действия релаксационных генераторов основан на зарядно-разрядных или накопительно-поглощающих явлениях, протекающих в широкополосных энергоемких цепях положительной обратной связи.
