Отклик нелинейной цепи на гармонический сигнал.

 

Как уже отмечалось ранее, существенно упростить анализ процессов в нелинейной радиоэлектронной цепи удается при ее теоретическом представлении последовательно соединенными безынерционным нелинейным элементом и линейной цепью – фильтром. Проанализируем физические процессы, протекающие в нелинейной цепи (рис.2.4. а), при воздействии на вход безынерционного нелинейного элемента z гармонического сигнала u₁(t)=U_mcosωt и постоянного напряжения смещения U_o. Испоьзуя вольтамперную характеристику нелинейного элемента и проведя несложные графические построения, найдем аналитическую запись формы тока в радиоэлектронной цепи в зависимости от фазового угла ν=ωt (рис. 2.4, б, в). Вследствие нелинейности характеристики форма тока на выходе цепи становится несинусоидальной. Причину этого искажения гармонического колебания нетрудно пояснить следующим образом. Так как ток и напряжение связаны линейной зависимостью ∆i = S ∆u, а крутизна ВАХ на разных участках неодинаковая (имеет нелинейный характер), то равным приращениям напряжения отвечают неравные приращения тока.

Рис. 2.4. Цепь с нелинейным элементом:

а – схема; б, в – графики процессов.

Поскольку функция тока обладает периодичностью (рис.2.4, в), то ее можно представить тригонометрическим рядом Фурье:

i(t)=I_o+ I_ncosnωt. (2.5)

Здесь I_o и I_n – амплитуды постоянной и гармонических составляющих.

 

Спектр тока в цепи с НЭ при степенной аппроксимации. Пусть суммарное напряжение источников смещения и входного гармонического сигнала

u(t)=U_o+U_mcosωt (2.6)

приложено к нелинейному элементу, вольтамперная характеристика которого в окрестности рабочей точки аппроксимирована полиномом Тэйлора вида:

i(u)=a_o+a₁(u-U_o)+a₂(u-U_o)²+a₃(u-U_o)³+… (2.7)

Подставив формулу (2.6) в (2.7), получим

i(u)=a_o+a₁U_mcosωt+a₂U_m²cos²ωt+ a₃U_m³cos³ωt+…

Используя известные формулы разложения степеней косинусов:

cos²x= (1+cos2x); cos³x= (3cosx+cos3x); cos⁴x= (3+4cos2x+cos4x); и т.д.

запишем общее выражение для тока нелинейной цепи, сгруппировав отдельно постоянные составляющие и все члены с косинусами одинаковых аргументов:

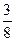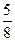i(t)=(a_o+ a₂U_m²+ a₄U_m⁴+…)+(a₁U_m+ a₃U_m³+ a₅U_m⁵+…)cosωt+( a₂U_m²+

a₄U_m⁴+…)cos2ωt+( a₃U_m³+ a₅U_m⁵+…)cos3ωt+… (2.8)

Представленное в более компактной форме соотношение (2.8) примет вид

i(t)=I_o+I₁cosωt+ I₂cos2ωt+ I₃cos2ωt+ … (2.9)

Здесь постоянная составляющая и амплитуды гармоник тока:

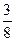I_o=a_o+ a₂U_m²+ a₄U_m⁴+…;

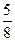I₁= a₁U_m+ a₃U_m³+ a₅U_m⁵+…;

I₂= a₂U_m²+ a₄U_m⁴+…;

I₃= a₃U_m³+ a₅U_m⁵+…. (2.10)

Анализ состава этих формул показывает, что при степенной аппроксимации гармонический состав тока в цепи с НЭ существенно зависит от степени полинома. При этом постоянная составляющая и амплитуды четных гармоник определяются четными, а амплитуды нечетных гармоник – нечетными коэффициентами степенного полинома.

Спектр тока в цепи с НЭ при кусочно-линейной аппроксимации его характеристики. Пусть суммарное гармоническое и постоянное напряжение вида (2.6) подается на вход электрической цепи с НЭ, характеристика которого аппроксимирована кусочно-линейной линией и описывается формулой (2.4). В этом случае временная диаграмма тока, протекающего через НЭ цепи, имеет форму косинусоидальных импульсов с отсечкой их нижней части (рис. 2.5).

 

 

Рис. 2.5. Форма тока при кусочно-линейной аппроксимации характеристики НЭ.

 

Параметр θ (в радианах или градусах), при котором ток изменяется от максимального значения I_m до нуля, называется углом отсечки. Изменение фазы, соответствующее длительности полного импульса тока на выходе цепи, равно 2θ. Из графиков на рис. 2.5. нетрудно определить, что при фазовом угле ωt=0 напряжение начала характеристики Е_н=U_o+U_mcosθ, откуда

сosθ=(Е_н- U_o)/ U_m (2.11)

Подставив в формулу (2.4) суммарное напряжение источников сигнала и смещения из выражения (2.6) и напряжение начала характеристики Е_н, получим аналитическую запись формы тока в зависимости от фазового угла:

i(ωt)=SU_m(cosωt-cosθ), -θ<ωt<θ (2.12)

Полученную четную функцию i(ωt) периодической последовательности импульсов тока (2.12) можно разложить в тригонометрический ряд Фурье, в котором период повторения составляет 2π, длительность импульса – 2θ, а текущий переменной является мгновенный фазовый угол ν= ωt. В этих импульсах тока постоянная составляющая запишется следующим образом:

I_o= (cosωt-cosθ)dωt= (sinθ-θcosθ). (2.13)

Амплитуда первой гармоники

I₁= (cosωt-cosθ)cosωtdωt= (θ-sinθcosθ). (2.14)

Подобным же образом определяются амплитуды гармонических составляющих I_n и для n=2,3, …. При этом обобщенная формула для вычисления этих гармоник будет:

I_n= . (2.15)

В радиотехнике полученные результаты принято записывать в специальной форме:

I_o=SU_mγ_o; I₁=SU_mγ₁; …; I_n=SU_mγ_n; (2.16)

Здесь γ_o, γ₁, …, γ_n – так называемые функции Берга, или коэффициенты гармоник, отражающие величины присутствующих гармоник в спектре преобразованного тока, которые аналитически выглядят следующим образом:

γ_n= (sinθ-θcosθ),

γ_n= (sinθ-θcosθ),

γ_n= , n=2.3, … (2.17)

 

Пример 2.3. Характеристика нелинейного элемента имеет кусочно-линейную аппроксимацию двумя отрезками, у которой Е_н=0,6 В, S=0,25 мА/в. На элемент воздействует суммарное (постоянное и переменное) напряжение u(t)=0,2+0,8cosωt В. Определить постоянную составляющую и первую гармонику тока, протекающих через нелинейный элемент цепи.

 

Решение. Воспользовавшись формулой (2.11), находим, что cosθ=0,6- 0,2)/0,8=0,5. Отсюда угол отсечки тока, протекающий через нелинейный элемент, θ=60^о. Два первых коэффициента гармоник, соответствующие этому углу, будут γ_о=0,11; γ₁=0,2. Подставив последовательно эти значения в соотношение (2.16), вычисляем соответственно амплитуды постоянной составляющей и первой гармоники: I_o=2 мА, I₁=4 мА.

Коэффициенты гармоник очень часто используются в инженерных расчетах, например, при проектировании схем нелинейных усилителей мощности, умножителей частоты и автогенераторов. Поэтому они приводятся в специальной технической литературе.

Лекция №10.