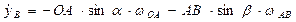
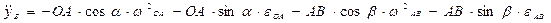
Для определения скорости и ускорения точки С следует составить уравнения выдвижения в координатной форме, проецируя радиус-вектор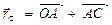 
на оси х и у.
V. Кинематический анализ движения твердого тела,
катящегося без скольжения по неподвижной поверхности
И имеющего неподвижную точку. Задание К.4.
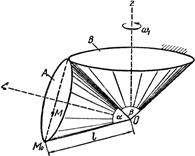
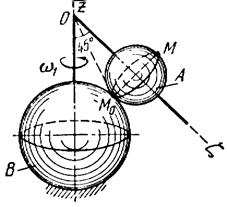
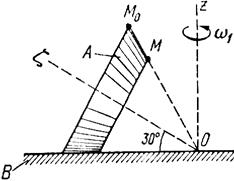
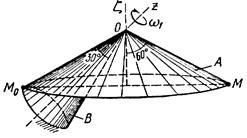
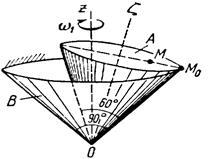
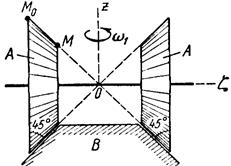
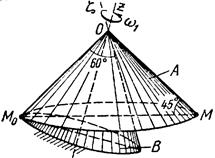
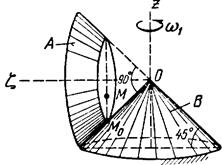
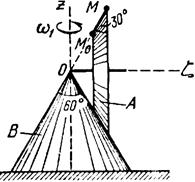
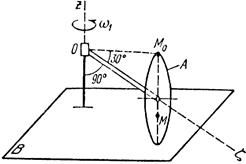
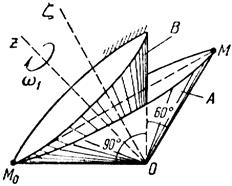
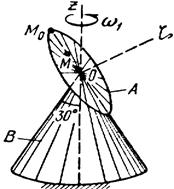
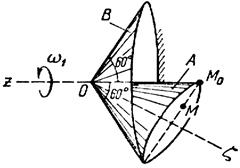
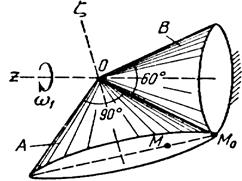
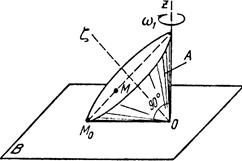
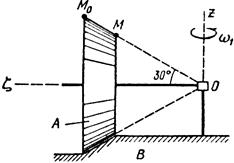
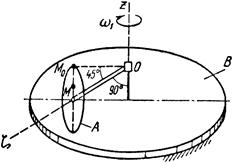
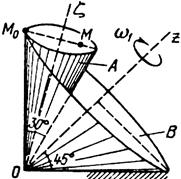
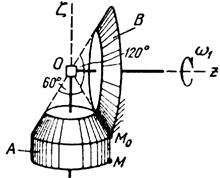
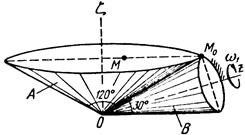
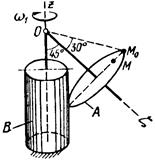
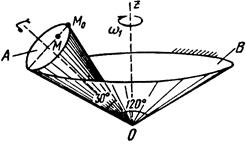
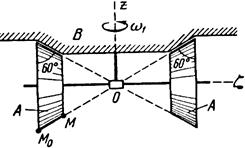
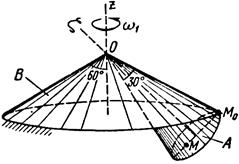
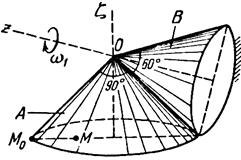
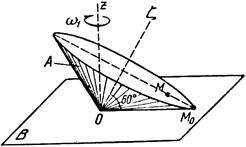
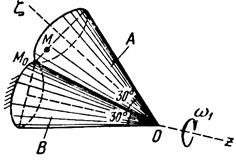
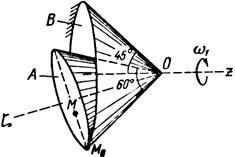
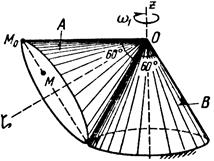
Тело А катится без скольжения по поверхности неподвижного тела В, имея неподвижную точку О. Ось Oz тела А вращается вокруг неподвижной оси Oz и имеет при заданном положении тела А угловую скорость w1 и угловое ускорение e1.
Определить угловую скорость и угловое ускорение тела А, а также скорость и ускорение точки М в указанном положении тела А.
Схемы показаны, на рис. 19-21, а необходимые для расчета данные приведены в табл. 9.
Таблица 9
| № варианта (рис. 19-21) | OM0, см | w1 рад/с | e1, рад/с2 | M0M, см | № варианта (рис. 19-21) | OM0, см | w1 рад/с | e1, рад/с2 | M0M, см |
| 2,3 | 4,0 | 2,4 | 5,4 | ||||||
| 3,0 | 3,0 | 3,5 | -3,0 | ||||||
| 1,2 | -3,6 | — | 1,0 | 2,2 | |||||
| 2,0 | 4,2 | 2,7 | 4,4 | ||||||
| 0,8 | 2,0 | 3,3 | -4,6 | ||||||
| 4,0 | 5,6 | 4,0 | -5,0 | ||||||
| 1,5 | -2,5 | — | 1,6 | 2,8 | |||||
| 2,1 | 3,2 | 2,0 | 3,7 | ||||||
| 3,2 | -4,7 | 3,5 | 4,1 | ||||||
| 1,3 | 1,8 | 1,6 | -3,0 | ||||||
| 0,9 | 2,6 | 2,2 | 3,3 | ||||||
| 2,2 | 3,0 | — | 4,1 | -5,5 | |||||
| 3,8 | 4,3 | 3,0 | 4,2 | ||||||
| 1,4 | -2,8 | 1,4 | 3,6 | ||||||
| 0,7 | 2,2 | 2,9 | -5,2 |
Примечание. Положительный и отрицательный знаки у e1 означают соответственно, что вращение оси Oz вокруг оси Oz происходит в направлении, показанном на схеме, ускоренно или замедленно.
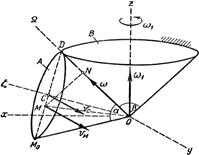
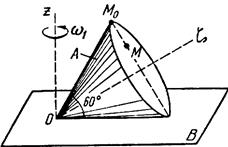
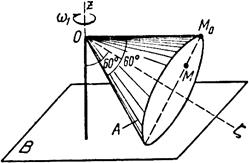
Пример выполнения задания. Тела А и В представляют собой прямые круговые конусы (рис. 22).
Дано: a = 60°, (b = 90°, ОМ0 = l = – 30 см, w1= 1,2 рад/с, e1 = 2,7 рад/с2,М0М = 10 см.
Решение. 1. Определение угловой скорости тела. Конус А совершает сферическое движение. Мгновенная ось вращения ОW совпадает с общей образующей конусов (рис. 23).
Выберем направления координатных осей Ох и Оу так, чтобы ось Oz, а следовательно, и ОW находились в плоскости xOz.
Скорость vc точки С является вращательной скоростью вокруг мгновенной оси.
| 
| 
|
| Рис. 22 | Рис. 23 | Рис. 24 |
Следовательно,
 ,
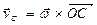| (1) |
где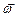 
— угловая скорость тела А.
С другой стороны,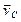 
— вращательная скорость вокруг оси Oz, поэтому
 ,
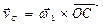| (2) |
Из (1) и (2) следует
 ,
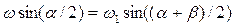| (3) | ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| Рис. 19. | |||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| Рис. 20. | |||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| Рис.21 | |||||
С учетом исходных данных находим ω = 2,32 рад/с.
Направление 
определяется направлением 
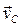в соответствии с (1).
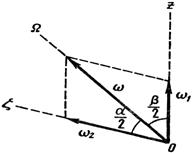
Угловую скорость тела А можно найти также путем сложения вращений вокруг пересекающихся осей — построением параллелограмма угловых скоростей (рис. 24):
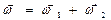
Здесь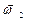 
– угловая скорость конуса А во вращении вокруг собственной оси Oz.
По теореме синусов,
,
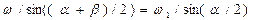что совпадает с выражением (3).
2. Определение углового ускорения тела. Угловое ускорение
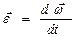
| (4) |
Вектор угловой скорости запишем в виде
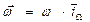
| (5) |
где ω – модуль вектора ;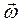 
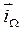– орт его направления. Следовательно,
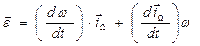
| (6) |
Заметим, что
|
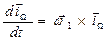
а с учетом направлени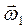й 
и 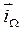(рис. 25)
|
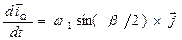
Теперь вместо (6) имеем
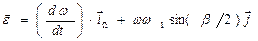
| (7) |
или
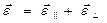
| (8) |
где
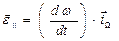
| (9) |
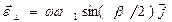
| (10) |
Эти же выражения составляющих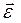 
непосредственно следуют из условия, что угловое ускорение геометрически равно скорости 
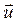конца вектора 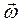. Её составляющие 
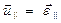и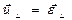 
- соответственно радиальная и трансверсальная (поперечная) скорости этой точки.
Вектор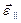 
направлен по мгновенной оси вращения ОΩ. Его модуль
.
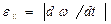Согласно (3) и учитывая, что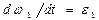 
,
,
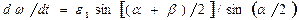или с учетом исходных данных
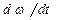= 5,22 рад/с2. Следовательно, 
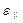= 5,22 рад/с2.
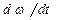Знак «+» при (при 
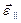) показывает, что направления и 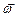совпадают.
Вектор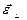 
, как следует из (10), имеет направление орта 
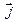. Его модуль
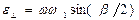или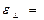 
1,97 рад/с2.
Так как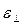 
и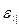 
взаимно перпендикулярны, то
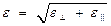или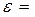 
5,58 рад/с2.
Векторы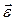 
, 
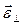и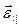 
показаны на рис. 25.
3. Определение скорости точки тела. Скорость точки М определяем как вращательную вокруг мгновенной оси:
 .
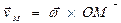| (11) |
Векторы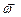 
и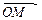 
расположены в плоскости xOz; следовательно, вектор 
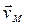параллелен оси Оу. Он имеет одинаковое направление с вектором 
;
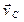Модуль скорости
 .
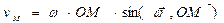| (12) |
Как видно из рис. 23,
;
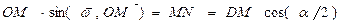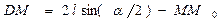
С учетом этих соотношений по формуле (12) находим
vM = 40,2 см/с.
4. Определение ускорения точки тела. Ускорение точки М находим как геометрическую сумму осестремительного и вращательного ускорений:
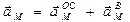
Осестремительное ускорение
.
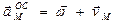Oно направлено по перпендикуляру к мгновенной оси вращения (рис. 25). Его модуль
.
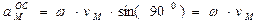Вращательное ускорение
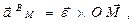
или, учитывая (9),
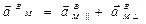, где
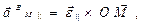
| (13) |
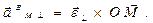
| (14) |
Сравнивая (13) с (11) и принимая во внимание, что направления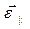 
и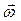 
совпадают, заключаем, что и направления 
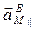и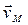 
тоже совпадают.
Модуль составляющей ускорения точки M.
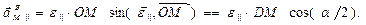
Вектор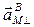 
расположен в плоскости xOz и перпендикулярен ОМ. Его модуль
.
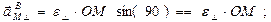
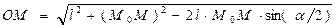В результате вычислений находим:
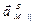= 90,4 см/с2; 
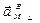= 52,2 см/с2.
Ускорение точки М найдем как геометрическую сумму трех составляющих:
.
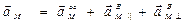Векторы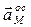 
и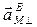 
расположены в плоскости xOz, а вектор 
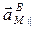ей перпендикулярен.
Поэтому модуль ускорения точки М (рис. 20)
.
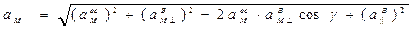Здесь
.
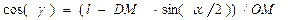| Окончательно после вычислений получаем: ам =110,9 см/с2. |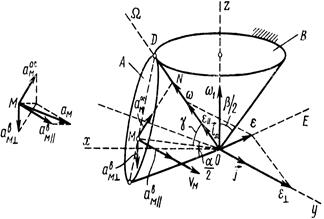 
|
| Рис. 25 |
