При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.
1.Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение ε определяем путем дифференцирования их по времени, т.е.
2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (7)
ω= vA/AP где А-точка плоской фигуры; Р мгновенный центр скоростей.Дифференцируем ω по времени, получаем
Так, например, при качении колеса без скольжения по неподвижной прямой линии (см. рис. 55), если за точку А взять центр колеса О, то, учитывая, что он движется прямолинейно, получим: ε= ao/R, так как в этом случае
OP=R = const и аτо = ао,
где R — радиус колеса.
При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью ω1 подвижного колеса и угловой скоростью ю кривошипа ОА (рис. 61). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес,
получаем
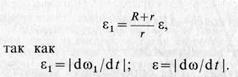где R — радиус неподвижного колеса; r —радиус подвижного колеса. Дифференцируя по времени (21), имеем
Из сравнения (21) и (22) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.
При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа ОА. При внутреннем зацеплении колес дуговые стрелки ε и ω колеса и кривошипа имеют противоположные направления.
3. Иногда угловое ускорение е можно найти путем проецирования на оси координат известного по направлению ускорения, например точки В, если ускорение какой-либо яругой точки А и угловая скорость фигуры ω известны или их можно вычислить предварительно.
Так, если ускорение точки В
ав = аА + а-τВА + апВА, (23)
то, проецируя обе части (23) на ось Ох, перпендикулярную ускорению ав, получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.
Задание для выполнения по разделу кинематика
II. Определение скорости и ускорения точки по заданным уравнениям
ее движения. Задание К.1.
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 1.
Таблица 1
| Номер варианта | Уравнения движения | t1, c | |
| x=x(t), см | y=y(t), ñì | ||
| -2t2+3 | -5t | 1,5 | |
| 4соs2(pt/2)+2 | 4sin2(pt/2) | ||
| -cos(pt2/3)+3 | sin(pt2/3)-l | ||
| 4t+4 | -4/(t+1) | ||
| 2sin (pt/2) | -3соз(pt/2)+4 | ||
| 3/t2+2 | -4/t | 1,5 | |
| 3t2-t+1 | 5t2-5t/2-2 | ||
| 7sin(pt2/4)+3 | 2-7cos(pt2/4) | ||
| -3/(t+2) | 3t+6 | ||
| -4cos(pt/2) | -2sin(pt/2)-3 | ||
| -4/t2+1 | -3/t | 1,5 | |
| 5sin2(pt/4) | 5cos2(pt/4)-3 | ||
| 5cos(pt2/3) | -5sin(pt2/3) | ||
| -2t-2 | -2/(t+l) | ||
| 4соs(pt/2) | -3sin(pt/2) | ||
| 3t | 4t2+1 | 1,5 | |
| 7sin2(pt/4)-5 | -7cos2(pt/4) | ||
| 1+3cos(pt2/3) | 3+3cos(pt2/3) | ||
| 4t2-4 | 3t | ||
| 2-3t-6t2 | 3-3t/2-3t2 | ||
| 6sin (t2/4)-2 | 6cos(pt2/4)+3 | ||
| 7t2-3 | 5t | 0,75 | |
| 4-3t2 | 4-5t2-5t/2 | ||
| -4cos(pt/2)-1 | -4sin(pt/2) | ||
| -6t | -2t2-4 | ||
| 8cos2(pt/4)+2 | 8sin2(pt/4)-7 | ||
| -3-9sin(pt2/4) | -9cos(pt2/4)+5 | ||
| -4t2+1 | -3t | ||
| 5t2+ 5t/2-3 | 3t2+t+3 | ||
| 2cos(pt2/3)-2 | 2sin(pt2/3)+3 |
Пример выполнения задания. Исходные данные:
| x = 4t; у=16t2-1; t1 = 0,5 (х и у — в см, t и t1 — в с). | (1) |
| Решение. Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1). Получаем у = х2 - 1, т. е. траекторией точки является парабола, показанная на рис. 6. Вектор скорости точки | 
| ||
| Рис. 6 | |||
| (2) | ||
Вектор ускорения
|
Здесь 
— орты осей x и у; 
— проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
| 
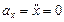
| (3) |
| 
|
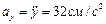
По найденным проекциям определяются модуль скорости:
| (4) |
и модуль ускорения точки:
| (5) |
Модуль касательного ускорения точки
| (6) |
или
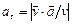
| (6`) |
| 6`` |
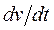выражает проекцию ускорения точки на направление ее скорости. Знак “+” при 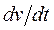означает, что движение точки ускоренное, направления 
и 
совпадают; знак “-” — что движение замедленное.
Модуль нормального ускорения точки
| (7) |
Если радиус кривизны траектории r в рассматриваемой точке неизвестен, то 
можно определить по формуле
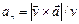
| (8) |
При движении точки в плоскости формула (8) принимает вид
| (8`) |
Модуль нормального ускорения можно определить и следующим образом:
| (9) |
После того как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения
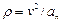
| (10) |
Результаты вычислений по формулам (3)-(6), (8) и (10) для заданного момента времени t1 =0,5 с приведены в табл. 2.
Таблица 2
| Координаты, см | Скорость, см/с | Ускорение, см/с2 | Радиус кривизны, см | |||||||
| x | y | vx | vy | v | ax | ay | a | at | an | r |
| 2,0 | 3,0 | 4,0 | 16,5 | 32,0 | 32,0 | 31,0 | 7,8 | 35,0 |
На рис. 6 показано положение точки М в заданный момент времени. Вектор v строим по составляющим vx и vy причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор а строим по составляющим ax и ay и затем раскладываем на составляющие an и at. Совпадение величин an и at найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 1) добавляется третье уравнение (табл. 3).
Общий порядок выполнения задания в этом случае такой же, как и в приведенном выше примере.
Таблица 3
| № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см |
| 3t | 3t | 2t | 1,5t | 4t | 6t | ||||||
| 2t | 2,5t | 3t | 5t | t | 3,5t | ||||||
| 1,5t | 5t | 1,5t | 3,5t | 1,5t | 4t | ||||||
| 4t+4 | 4t+8 | 2t+2 | 6t | 6t | 5t | ||||||
| t | T | 3t | 2t | 2t | 1,5t |
III. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях. Задание К.2.
Движение груза 1 должно описываться уравнением
| х = c2t2 + c1t + с0, | (1) |
где t — время, с; с0-2 — некоторые постоянные.
В начальный момент времени (t=0) координата груза должна быть х0, а его скорость — v0.
Кроме того, необходимо, чтобы координата груза в момент времени t = t2 была равна х2.
Определить коэффициенты с0, с1 и c2 при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1 скорость и ускорение груза и точки М одного из колес механизма.
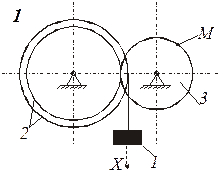
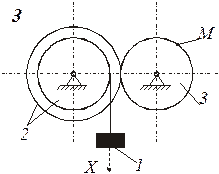
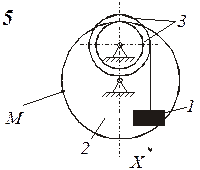
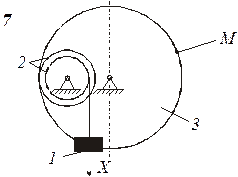
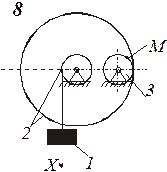
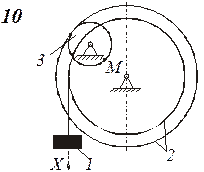
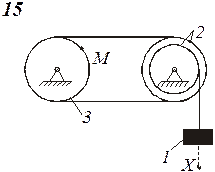
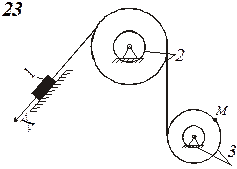
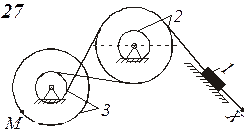
Схемы механизмов показаны на рис. 8-10, а необходимые данные приведены в табл. 4.
Таблица 4
| Номер варианта (рис.2-4) | Радиусы, см | Координаты и скорости груза 1 | Расчетные моменты времени, с | ||||||
| R2 | r2 | R3 | r3 | x0, см | v0, см/с | x2, см | t2 | t1 | |
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| _ | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — | |||||||||
| — |
| 
|
| 
|
| 
|
| 
|
| 
|
Рис.8
| 
|
| 
|
| 
|
| 
|
| 
|
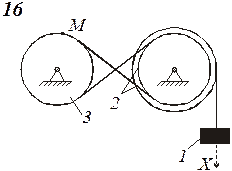
Рис.9
| 
|
| 
|
| 
|
| 
|
| 
|
Рис. 10
Пример выполнения задания. Дано: схема механизма (рис.7); R2=50 см, r2=25 см, R3=65 см, r3=40 см, x0=14 см, v0=5 см/с, x2=168 см, t1=1 с, t2=2 с.
| Найти уравнение движения груза, а также скорости и ускорения груза и точки М в момент времени t=t1. Решение. Уравнение движения груза 1 имеет вид x=c2t2+c1t+c0 (1) Коэффициенты с0, с1 и с2 могут быть определены из следующих условий: | 
| ||
| Рис. 7 | |||
| при t = 0 | х0 = 14 см |  = 5 см/с
| (2) |
| при t2 = 2с | х2 = 168 см | (3) |
Скорость груза 1
v = 
= 2c2t + c1. (4)
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты
с0 = 14 см, с1= 5 см/с, с2 = 36 см/с2.
Таким образом, уравнение движения груза 1
х = 36t2 + 5t + 14. (5)
Скорость груза 1
v = = 72t + 5. (6)
Ускорение груза 1
а = 
= 72 см/с2.
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес w2 и w2 .В соответствии со схемой механизма
| v=r2w2, R2w2=R3w3 | (7) |
откуда
w3=vR2/r2R3,
или с учетом (6) после подстановки данных
w3=2,215t+0,154.
Угловое ускорение колеса 3
e3= 
=2,215 рад/с2.
Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам
vm= R3w3;
; 
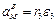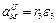
| Результаты вычислений для заданного момента времени t1=1с приведены в табл. 5. Скорости и ускорения тела 1 и точки М показаны на рис.11. |
| Рис. 11 |
Таблица 6
| v, см/с | а, см/с2 | w3, рад/с | e3, рад/с2 | vM, см/с |  , см/с2
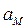|  , см/с2
|  , см/с2
|
| 2,37 | 2,22 | 94,8 | 88,6 |
