Система параллельных сил (рис.25) приведем к произвольному центру О, получим в этом центре силу R*, равную главному вектору, и пару сил с момента М.
Направили ось У параллельно силам, тогда проекции главного вектора на координатные оси
Rx= ∑Fx=O; Ry=∑Fy= ±Piy
Так как Rx=O, то главный вектор направлен по оси У. Отсюда можно сделать вывод, что главный вектор системы параллельных сил параллелен силам, его модуль равен алгебраической сумме проекции сил на ось, параллельную силам, а его направление определяется знаком этой суммы.
Момент пары сил равен главному моменту параллельных сил относительно центра приведения: М=М0= М10+М20+….Мn0
или
М=Мi0
Для системы параллельных сил плоскости имеем два условия равновесия.
М=0 и R*=0.
Два условия равновесия системы параллельных сил на плоскости можно выразить в виде двух уравнений:
или 
при этом прямая АВ не должна быть параллельна силам.
Сложение параллельных сил в пространстве.
Для сложения параллельных сил P1,P2….Pn приложенных в точках A1,A2….An выберем произвольный центр приведения О.
После приведения системы cил к этому центру получим силу, приложенную в центре приведения и равную главному вектору заданных сил R*, и пару сил с моментом М, равным главному моменту Мо всех сил относительно центра приведения О.
Проведем через, центр приведения О три взаимно перпендикулярные оси х, у, z, направив ось z параллельно рассматриваемым силам (рис. 26).
Вычислим проекции главного вектора на оси координат
|
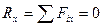
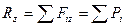
Так как проекции всех сил на оси Х и У равны нулю, то главный вектор R* направлен по оси Z.
Вычислим проекции главного момента М0 относительно начала координат на оси x,y,z как главные моменты сил относительно этих осей:
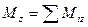
Так как заданные силы параллельны оси z, то Mz=0 и главный момент M0 рассматриваемой системы сил лежит в плоскости xOy, т.е. направлен перпендикулярно главному вектору R*.
Модуль главного момента:
Для системы параллельных сил в пространстве имеются два условия равновесия сил:
M0=0; R*=0
Если взаимно уравновешивающиеся силы параллельны оси z, то
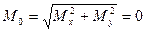
т.е.
Mx=∑Mix=0 и My=∑Miy=0
а так же
Таким образом, для системы сил, параллельных оси z, имеем три уравнения равновесия
∑Mix=0 ∑Miy=0 ∑Zi=0
Равновесие рычага.
Рычагом называется твердое тело, которое может вращаться вокруг неподвижной оси под действием сил, лежащих в одной плоскости, перпендикулярной к этой оси (рис 27)
Равновесие рычага будет только в том случае, если сумма моментов всех сил приложенных к нему сил относительно неподвижной точки рычага равна нулю.
Условие равновесия:
P2h2-P1h1=0
Способность тела сопротивляться всякому, хотя бы и малому, нарушению его равновесия называется статической устойчивостью. Из условия равновесия сил, действующих на рычаг, получим условие устойчивости тел при опрокидывании. Положим, что к прямоугольному параллелепипеду весом G на высоте d приложена горизонтальная сила, которая может не только сдвинуть тело, но и опрокинуть его вращением вокруг ребра А. Считая, что сила Р недостаточно велика, чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие (рис 28)
Обозначим через α расстояние до точки А, изображающей на чертеже ось вращения рычага, до линии действия силы G, которая препятствует опрокидыванию. Составим сумму момент задаваемых сил и G относительно опорной точки А:
Ga-Pd=0
откуда
Ga=Pd
Назовем абсолютные величины моментов сил G и Р относительно точки А соответственно Задерживающим и опрокидывающим моментами:
Mуд.=Ga Mопр.=Pd
Тогда на границе устойчивости получим:
Mуд.=Mопр.
Устойчивость при опрокидывании в технике принято определять соотношением величины удерживающего момента к величине опрокидывающего момента:
Это отношение называется коэффициентом устойчивости.
Очевидно, что в случае предельной устойчивости коэффициент устойчивости равен единице, а в случае устойчивого состояния К >1.
