Теорема 3. Граф G=(X,.A) містить гамільтоновий цикл. якщо
п ³ 3 і d(xk) £ k £ 1/2 n ® d(xn-k) ³ n - k. (2)
Умову (2) легко перевірити. Необхідно впорядкувати вершини за зростанням їх степенів і перевірити чи виконується умова для перших n/2 вершин.
Розглянемо тепер методи розрахунку нижніх границь довжини оптимальних гамільтонових контурів на орієнтованому графі G = (X, A). Якщо від довжини довільного гамільтонового контуру відняти значення нижньої границі, то отримана різниця дорівнює максимальному значенню, на яке довжина гамільтонового контуру може перевищувати довжину оптимального гамільтонового контуру. Значення цієї вершини потрібно для оцінки різниці довжин знайденого і оптимального гамільтонового контуру.
Для орграфу дуги, що входять в гамільтоновий контур, повинні володіти наступними двома властивостями:
1. Кожна вершина повинна бути інцидентна двом іншим дугам, одна з яких направлена до неї, а інша - від неї;
2. Всі дуги повинні бути зв'язані. Дуги, які входять в будь-яку множину незв'язаних контурів, що містять всі вершини, володіють властивістю 1.
Будь-яка зв'язана множина дуг володіє властивістю 2. І тільки гамільтоновий контур володіє одночасно властивостями 1 і 2.
Розглянемо сімейство F всіх підмножин множини А, які володіють властивістю 1. (Будемо вважати, що сімейство F не пуста множина). Зрозуміло, що кожен гамільтоновий контур входить в F. Отже, нижньою границею довжини оптимального гамільтонового контуру є найменше значення суми довжин дуг, які утворюють підмножини в F. Позначимо через L1 цю нижню границю. Нижню границю оптимального гамільтонового контуру можна обчислити за алгоритмом.
Крок 1. На основі графу G будується граф G'=(X', A').
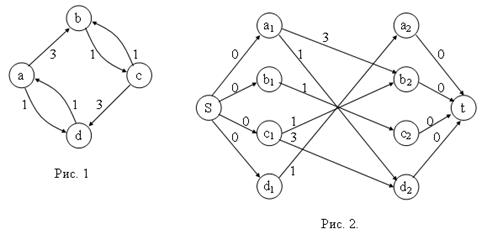
Для цього кожній вершині х, що належить множині X ставиться у відповідність пара вершин х1ÎX' і х2ÎX'. Кожній дузі (х, у)ÎА ставиться у відповідність проміжна дуга (х1, у2)ÎА'. Нехай кожна проміжна дуга має пропускну здатність, яка дорівнює 1, вартість, що дорівнює довжині відповідної дуги в А. Введемо вершину-джерело "s" і вершину-стік "t" і з'єднаємо вершину "s" з направленими з неї дугами (s, х1) з кожною з вершин х1ÎХ'. З'єднаємо вершину "t" з кожною з вершин х2ÎХ' направленими в неї дугами (х2, t). Нехай кожна з дуг (s, x1) і (х2, t) для всіх х1 і х2ÎX має пропускну здатність, яка дорівнює 1, і нульову вартість.
Крок 2. Визначимо на графі G' максимально можливий потік з "s" в "t", що має мінімальну загальну вартість. Такий потік шукається за допомогою алгоритму побудови потоку мінімальної вартості. Нехай L1 дорівнює вартості отриманого потоку. Оскільки пропускні здатності всіх дуг у графі G' дорівнюють 1, отриманий потік складається з одиничних потоків, що протікають у дугах графу G' від вершини "s" до "t". Крім того, кожна з проміжних вершин інцидентна не більше ніж одній дузі, по якій протікає одиничний потік. Далі, кожній проміжній дузі в А' відповідає деяка дуга в А. Розглянемо множину всіх проміжних дуг, по яких протікає одиничний потік. Нехай через М позначимо відповідну множину дуг в А. Дуги в множині М утворюють незв'язні контури в G. Інакше існувала би деяка вершина хÎХ, яка не була б інцидентна направленій до неї чи з неї дуги в М. Це відповідало б тому, що в графі G' у вершину "х2" не входив би чи з вершини "x1" не виходив би ні один з одиничних потоків. У кожному з цих двох випадків сумарний потік з "s" в "t" складався б менше ніж з |Х| одиничних потоків. Але це неможливо, оскільки кожній підмножині в F відповідає потік у G', який дорівнює |Х| одиниць, і крім того F не пуста множина. Оскільки ненульову вартість мають лише проміжні дуги, то сумарна вартість знайденого потоку дорівнює сумі довжин дуг, які входять у відповідні підмножини в F. Оскільки знайдений потік має найменшу сумарну вартість, то відповідна йому підмножина в F повинна мати мінімальну суму довжин дуг. Отже, L1 є нижньою границею довжини оптимального гамільтонового контуру в графі G.
Якщо в граф G входять неорієнтовані дуги, то кожну неорієнтовану дугу можна замінити парою протилежно направлених дуг, які з'єднують цю ж пару вершин. Нехай кожна з цих направлених дуг має довжину, що дорівнює довжині неорієнтованої дуги. Граф, який при цьому отримується, міститиме лише направлені дуги і для нього можна застосувати описаний вище метод обчислення L1.
Якщо множина М утворює гамільтоновий контур, то ми знайшли не тільки нижню границю довжини оптимального гамільтонового контуру, але й сам оптимальний контур.






