МЕТОДИЧНІ ВКАЗІВКИ
з дисципліни «Інформатика інфокомунікаційних систем, ч. 2»
для студентів базового напряму 050902 «Радіоелектронні апарати»,
які навчаються заочно за скороченим терміном підготовки
в Інституті післядипломної освіти
(освітньо – кваліфікаційний рівень: бакалавр)
Затверджено
на засіданні кафедри
"Електронні засоби інформаційно-комп’ютерних технологій
Протокол №
від “ “ 2010 р.
Львів 2010
Методичні вказівки з дисципліни «Інформатика інфокомунікаційних систем, ч. 2» для студентів базового напряму 050902 «Радіоелектронні апарати», які навчаються заочно за скороченим терміном підготовки в Інституті післядипломної освіти (освітньо – кваліфікаційний рівень: бакалавр) / Укл. І.В. Атаманова. - Львів: НУ "ЛП", 2010. - 28 с.
Укладачі І.В. Атаманова, к. т. н., доц.
Відповідальний за випуск Т.А. Смердова, к. т. н., доц.
Рецензенти Є.В. Сторчун, д. т. н., проф.
ЗАГАЛЬНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
МНОЖИНИ
Елементи і множини
Множина – це будь-яка визначена сукупність об’єктів. Об’єкти, з яких складається множина, називаються її елементами.
Якщо об'єкт х є елементом множини S, ми пишемо хÎS (читається «х належить S»). Якщо х не належить S, пишемо хÏS. Можна задати множину переліком його елементів через коми у фігурних дужках. Наприклад, множина S={1,2,3} містить елементи 1,2,3 і лише їх. Число 2 є елементом цієї множини, а число 4 - ні, так що 2ÎS, 4ÏS. Множина не може містити двох однакових елементів, і порядок елементів не фіксований.
Дві множини А і В рівні, якщо вони складаються з одних і тих же елементів. В цьому випадку пишуть А=В.
Наприклад, {1,2,3,1} = {1,2,3} = {3,2,1}.
Для часто використовуваних множин є спеціальні позначення:
· Æ позначає порожню множину, що не містить жодного елементу;
· Z позначає множину цілих чисел; Z = {..., -2, - 1,0,1, 2,...};
· R позначає множину дійсних чисел;
· N позначає множину натуральних чисел; N = {0,1,2,...}. (Іноді нумерацію натуральних чисел починають з 1 - раніше так було прийнято.)
Якщо всі елементи множини А є елементами множини В (з хÎА слідує хÎВ), говорять, що А є підмножиною множини В і пишуть АÍВ. Якщо при цьому А не співпадає з В, то А називається власною підмножиною множини В; в цьому випадку пишуть АÌВ. (Багато авторів використовують позначення АÍВ для підмножин, а не для власних підмножин.) Для будь-якої множини А виконане співвідношення АÍА.
Множини А і В рівні тоді і тільки тоді, коли АÍВ і ВÍА.
Для будь-яких трьох множин А, В і С із АÍВ і ВÍС виходить АÍС.
Для будь-якої множини А має місце співвідношення Æ Í А.
Іноді множина визначається як частина іншої множини: ми можемо виділити з множини А всі елементи, що володіють деякою властивістю, і утворити з них нову множину В. Наприклад, множину парних чисел можна визначити як {х: хÎZ і х/2 - ціле число }. Це звичайно читають «множина х з Z, для яких х/2 - ціле число». Іноді замість двокрапки використовується вертикальна риска.
Об’єднанням А і В називається множина С, яка складається із елементів множин А або В. Позначається C = AÈB. Запис yÎAÈB тотожний (замість слова тотожний далі будемо використовувати символ º) запису yÎA або yÎB.
Отже, yÎAÈB º yÎA або yÎB.

Наприклад, якщо A ={транзистор, резистор}, В ={конденсатор, індуктивність}, то C = AÈB = {транзистор, резистор, конденсатор, індуктивність}.

Рис.1. Об’єднання C = A È B.
Перетином множин А і В називається множина С що складається з елементів, які належать до множин А і В. Позначається C = AÇB.
Отже, y Î A Ç B º y Î A і y Î B.
А 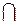 В:= {x½xÎA і xÎB}
В:= {x½xÎA і xÎB}

Рис. 2. Перетин C = AÇB.
Якщо множини А і В не мають спільних елементів, то їх перетин визначає пусту множину.
Різницею множин А і В називається множина С, яка складається із елементів, які належать А і не належать В. Позначуються C = A\B.
Запис y Î A\B º y Î A і y Ï B.
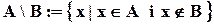

Рис. 3. Різниця C = A\B.
Симетричною різницею множин А і В називається множина С, яка складається із елементів, які належать А і не належать В або належать В і не належать А. Позначається АDВ.


Рис. 4. Симетрична різниця C = АDВ
Приклад. А:={1, 2, 3}; B:={3, 4, 5}.


A\B = {1, 2}; ADB={1, 2, 4, 5}.
ГРАФИ
Основні визначення
Графом G = (V, Е) називається сукупність двох множин – непорожньої множини V (множини вершин) і множини Е неупорядкованих пар різних елементів множини V (Е – множина ребер).
G = (V, Е) = áV; Eñ, V ≠ Æ, EÌV×V, E = E-1.
Число вершин графа позначимо p, а число ребер – q:
p:=p(G):=|V|, q:=q(G):= |E|.
Нехай v1, v2 – вершини, е = (v1, v2) – ребро, яке їх з’єднує. Тоді вершина v1 і ребро е інцидентні, вершина v2 і ребро е також інцидентні. Два ребра, інцидентні одній вершині, називаються суміжними; дві вершини, інцидентні одному ребру, також називаються суміжними.
Множина вершин, суміжних з вершиною v, називається множиною суміжності вершини v і позначається Г+(v):
Г+(v):={uÎV½(u, v)ÎE}, Г(v):= Г*(v):= Г+(v)È{v},
uÎГ(v)ÛvÎГ(u):
Звичайно граф зображають діаграмою: вершини – точками (або кружками), ребра – лініями.
В якості приклада розглянемо діаграму графа (мал. 1), який має чотири вершини і п’ять ребер.

Мал. 1. Діаграма графа
В цьому графі вершини v1 і v2, v2 і v3, v3 і v4, v4 і v1, v2 і v4 суміжні, а вершини v1 і v3 не суміжні. Суміжні ребра: е1 і е2, е2 і е3, е3 і е4, е4 і е1, е1 і е5, е2 і е5, е3 і е5, е4 і е5. Несуміжні ребра: е1 і е3, е2 і е4.
Інші визначення.
Якщо елементами множини Е являються упорядковані пари, то граф називається орієнтованим (або орграфом). В цьому випадку елементи множини V називаються вузлами, а елементи множини Е – дугами.
На мал. 2(а) показаний орієнтований граф з множиною вершин {1,2,3,4,5,6}. Вершини зображені кухлями, а ребра - стрілками. Слід відзначити, що граф може містити ребра - цикли, які сполучають вершину з собою.
У неорієнтованому графі G = (V, Е) множина ребер Е складається з невпорядкованих пар вершин: парами є множини {u, v}, де u, vÎV і u≠v. Позначатимемо неорієнтоване ребро як (u, v) замість {u, v}; при цьому для неорієнтованого графа (u, v) і (v, u) позначають одне і те ж ребро. Неорієнтований граф не може містити ребер-циклів, і кожне ребро складається з двох різних вершин («сполучаючи» їх).
На малюнку 2(б) зображений неорієнтований граф з множиною вершин {1,2,3,4,5,6}.
Багато понять паралельно визначаються для орієнтованих і неорієнтованих графів (з відповідними змінами). Про ребро (u,v) орієнтованого графа говорять, що воно виходить з вершини u і входить у вершину v.

Мал. 2. Орієнтовані і неорієнтовані графи.
(а) Орієнтований граф (V, E), де V={1, 2, 3, 4, 5, 6} і Е={(1, 2), (2, 2), (2, 4), (2, 5), (4, 1), (4, 5), (5, 4), (6, 3)}. Ребро (2, 2) є ребром-циклом;
(б) неорієнтований граф G=(V, Е), де V - {1, 2, 3, 4, 5, 6} і Е = {(1, 2), (1, 5), (2, 5), (3, 6)}. Вершина 4 є ізольованою (не має суміжних вершин);
(в) Підграф графа (а), що виходить шляхом обмеження графа (а) на множині вершин {1, 2, 3, 6}.
Елементи графів
Граф G¢=(V¢, Е¢) називається підграфом графа G=(V, Е) (позначається G¢ÌG), якщо V¢ÌV і/або E¢ÌE.
Якщо V¢=V то G¢ називається остовним підграфом G.
Кількість ребер, інцидент них вершині v, називається ступенем (або валентністю) вершини v і позначається d(v):
"vÎV 0 £ d(v) £ p-1, d(v) = |Г(v)|.
Якщо ступінь вершини дорівнює 0 (тобто d(v) =0), то вершина називається ізольованою. Якщо степінь вершини дорівнює 1 (тобто d(v) =1), то вершина називається кінцевою, або висячою. Наприклад, для графа на мал. 5(б) ступінь вершини 2 рівний 2.
Для орграфа число дуг, які виходять з вершини v, називається напівступенем виходу, а число дуг, які входять у вершину – напівступенем заходу. Позначаються ці числа відповідно – d-(v) та d+(v). Сума вхідних ступенів і вихідних ступенів називається ступенем вершини. Наприклад, вершина 2 в графі на мал. 2(а) має вхідний ступінь 2, вихідний ступінь 3 і ступінь 5.
Шлях довжини k з вершини u у вершину v визначається як послідовність вершин áv0, v1, v2,…,vkñ, в якій v0 = u, vk = v і (vi-1, vi)ÎЕ для всіх i = 1, 2,..., k. Таким чином, шлях довжини k складається з k ребер. Цей шлях містить вершини v0, v1, v2,…,vk і ребра (v0,v1), (v1,v2),…,(vk-1,vk). Вершину v0 називають початком шляху, вершину vk - його кінцем; говорять, що шлях веде з v0 в vk. Якщо для даних вершин u і u' існує шлях р з u в u', то говорять, що вершина u' досяжна з u по шляху р. В цьому випадку ми пишемо (для орієнтованих графів) u ~ u'.
Шлях називається простим, якщо всі вершини в ньому різні. Наприклад, на мал. 2(а) є простий шлях á1,2,5,4ñ довжини 3, а також шлях á2,5,4,5ñ тієї ж довжини, що не є простим.
Підшлях шляху р=áv0, v1, v2,…,vkñ вийде, якщо ми візьмемо деяку кількість вершин цього шляху, що йдуть підряд, тобто послідовність ávi, vi+1,…,vjñ при деяких i, j, для яких 0 £ i £ j £ k.
Циклом в орієнтованому графі називається шлях, в якому початкова вершина співпадає з кінцевою і який містить хоча б одне ребро. Цикл áv0, v1, v2,…,vkñ називається простим, якщо в ньому немає однакових вершин (окрім першої і останньої), тобто якщо всі вершини v0, v1, v2,…,vk різні. Ребро-цикл є циклом довжини 1. Ми ототожнюємо цикли, відмінні зрушенням уздовж циклу: один і той же цикл довжини k може бути представлений k різними шляхами (в якості початку і кінця можна узяти будь-яку з k вершин). Наприклад, на мал. 2(а) шляхи á1,2,4,1ñ, á2,4,1,2ñ і á4,1,2,4ñ представляють один і той же цикл. Цей цикл є простим, тоді як цикл á1,2,4,5,4,1ñ таким не є. На тому ж малюнку є цикл á2,2ñ, який утворений єдиним ребром-циклом (2,2). Орієнтований граф, який не містить ребер-циклів, називається простим.
У неорієнтованому графі шлях áv0, v1, v2,…,vkñ називається (простим) циклом, якщо k ³ 3, v0 = vk і всі вершини v1, v2,…,vk різні. Наприклад, на мал. 2(б) є простий цикл á1,2,5,1ñ.
Граф, в якому немає циклів, називається ациклічним.
Неорієнтований граф називається зв'язним, якщо для будь-якої пари вершин існує шлях з однієї в іншу.
Для неорієнтованого графа відношення «бути досяжним з» є відношенням еквівалентності на множині вершин. Класи еквівалентності називаються зв'язними компонентами графа. Наприклад, на мал. 2(б) є три зв'язні компоненти: {1,2,5}, {3,6} і {4}. Неорієнтований граф зв'язний тоді і тільки тоді, коли він складається з єдиної зв'язкової компоненти.
Орієнтований граф називається сильно зв'язним, якщо з будь-якої його вершини можна досягнути (по орієнтованих шляхах) будь-яку іншу. Будь-який орієнтований граф можна розбити на сильно зв'язні компоненти, які визначаються як класи еквівалентності відношення «u досягається з v і v досягається з u». Орієнтований граф сильно зв'язний тоді і тільки тоді, коли складається з єдиної сильно зв'язної компоненти. Граф на рис. 2(а) має три таких компоненти: {1,2,4,5}. {3} і {6}. Відзначимо, що вершини {3,6} не входять в одну сильно зв'язну компоненту, оскільки 3 досягається з 6, але не навпаки.
Для будь-якого неорієнтованого графа G можна розглянути його орієнтований варіант, замінивши кожне неорієнтоване ребро {u, v} на пару орієнтованих ребер (u, v) і (v, u), що йдуть в протилежних напрямах. З другого боку, для кожного орієнтованого графа можна розглянути його неорієнтований варіант, забувши про орієнтацію ребер, видаливши ребра-цикли і з'єднавши ребра (u, v) і (v, u) в одне неорієнтоване ребро {u, v}. У орієнтованому графі сусідом вершини u називають будь-яку вершину, сполучену з нею ребром (у ту або іншу сторону); таким чином, v є сусідом u тоді і лише тоді, коли v суміжно u або u суміжне v. Для неорієнтованого графа вираз «v - сусід u» і «v суміжна з u» є синонімами.
Деякі види графів мають спеціальні назви.
Повним графом називають неорієнтований граф, що містить всі можливі ребра для даної множини вершин (будь-яка вершина суміжна будь-якій іншою).
Неорієнтований граф (V, Е) називають дводольним, якщо множину вершин V можна розбити на дві частини V1 і V2 таким чином, що кінці будь-якого ребра опиняються в різних частинах.
Іноді розглядають узагальнення поняття графа. Наприклад, можна розглядати мультиграф, який схожий на неорієнтований граф, але може містити багато ребер, що сполучають одну і ту ж пару вершин, а також ребра-цикли.
Гіперграф відрізняється від неорієнтованого графа тим, що він містить гіперребра, що сполучають не дві вершини, а довільну множину вершин. Багато алгоритмів обробки звичних графів можуть бути узагальнені на такі графоподібні структури.
Дерева
Ациклічний неорієнтований граф називають лісом, а зв'язний ациклічний неорієнтований граф називають (вільним) деревом (деревом без виділеного кореня). Таким чином, компонентами зв’язності лісу є дерева.

Мал. 4. (а) Дерево без виділеного коріння. (б) Ліс. (в) Граф, що містить цикл, не є ні деревом, ні лісом.
На мал. 4(а) зображене дерево; на мал. 4(б) зображений ліс. Ліс на мал. 4(б) не є деревом, оскільки не зв'язний. Граф на мал. 4(в) не є ні деревом, ні навіть лісом, оскільки в ньому є цикл.
У наступній теоремі вказано декілька важливих властивостей дерев.
Теорема 2 (властивості дерев).
Хай G = (V, Е) - неорієнтований граф. Тоді наступні властивості рівносильні:
1) G є деревом (без виділеного коріння);
2) для будь-яких двох вершин G існує єдиний сполучаючий їх простий шлях;
3) граф G зв'язний, але перестає бути зв'язковим, якщо видалити будь-яке його ребро;
4) граф G зв'язний і |Е| = |V| - 1;
5) граф G ациклічний і |Е| = |V| - 1;
6) граф G ациклічний, але додавання будь-якого ребра до нього породжує цикл.
Дерева з корінням. Орієнтовані дерева
Орієнтованим деревом ( або ордеревом, або кореневим деревом) називають орграф з наступними властивостями:
1. існує єдиний вузол, напівстепінь заходу якого дорівнює 0. він називається коренем ордерева;
2. напівстепінь заходу всіх інших вузлів дорівнює 1;
3. кожен вузол досягається із кореня.
Дерево з корінням, або кореневе дерево, виходить, якщо в дереві (зв'язному ациклічному неорієнтованому графі) виділити одну з вершин, назвавши її корінням. На малюнку 6(а) показане кореневе дерево з 12 вершинами і корінням 7.

Представлення графів: діаграма, матриця суміжності, матриця інциденцій, матриця ваг, набір списків суміжних вершин
 Матриця суміжності. Представлення графа за допомогою квадратної булевської матриці, яка відображає суміжність вершин, називається матрицею суміжності, де
Матриця суміжності. Представлення графа за допомогою квадратної булевської матриці, яка відображає суміжність вершин, називається матрицею суміжності, де
1, якщо вершина vi суміжна з вершиною vj,
М[i,j] =
0, якщо вершини vi і vj не суміжні.
Матриця інциденцій. Представлення графа за допомогою матриці, яка відображає інцидентність вершин і ребер, називається матрицею інциденцій, де для неорієнтованого графа
 |
1, якщо вершина vi інцидентна ребру еj,
Н[i,j] =
0, у протилежному випадку.
а для орієнтованого графа
 |
1, якщо вершина vi інцидентна ребру еj і являється його кінцем,
Н[i,j] = 0, якщо вершина vi і ребро еj не інцидентні.
-1, якщо вершина vi інцидентна ребру еj і являється його початком.
Представлення графа G = (V, Е) у вигляді списків суміжних вершин використовує масив з |V| списків – по одному на вершину. Для кожної вершини uÎV список суміжних вершин містить в довільному порядку (вказівники на) всі суміжні з нею вершини (всі вершини v, для яких (u, v)ÎЕ).

Мал.. 1. Два представлення неорієнтованого графа:
(а) неорієнтований граф G з 5 вершинами і 7 ребрами;
(б) Представлення цього графа за допомогою списків суміжних вершин;
(в) Представлення цього графа у вигляді матриці суміжності.
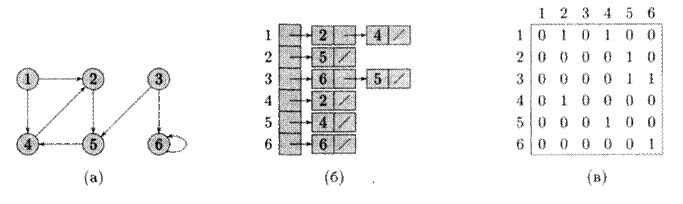
Мал. 2. Два представлення орієнтованого графа:
(а) Орієнтований граф G з 6 вершинами і 8 ребрами;
(б) Представлення цього графа за допомогою списків суміжних вершин;
(в) Представлення цього графа у вигляді матриці суміжності.
На мал. 1(б) показано представлення неорієнтованого графа мал. 1(а) за допомогою списків суміжних вершин. Аналогічне уявлення для орієнтованого графа мал. 2(а) зображене на мал. 2(б).
Для орієнтованого графа сума довжин всіх списків суміжних вершин рівна загальному числу ребер: ребру (u, v) відповідає елемент v списку Adj[u]. Для неорієнтованого графа ця сума рівна подвоєному числу ребер, оскільки ребро (u, v) породжує елемент в списку суміжних вершин як для вершини u, так і для v.
Списки суміжних вершин зручні для зберігання графів з вагами, в яких кожному ребру приписана деяка вага, тобто задана вагова функція w: E®R. В цьому випадку зручно зберігати вагу w(u, v) ребра (u, v)ÎЕ разом з вершиною v в списку вершин, суміжних з u. Так само можна зберігати і іншу інформацію, пов'язану з графом.
ЗАДАЧА ЛИСТОНОШІ






