Перед початком роботи алгоритму всі ребра вихідного графу є не розфарбовані і ні один з букетів не сформований. Нехай блакитний колір використовується для розфарбування ребер, що включаються в остовне дерево, а зелений – для розфарбування ребер, що не включається в дерево.
Крок 1. Вибрати довільне ребро, яке не є петлею. Зафарбувати це ребро в блакитний колір і сформувати букет, включивши в нього кінцеві вершини розфарбованого ребра.
Крок 2. Вибрати будь-яке нерозфарбоване ребро, яке не є петлею (якщо в графі такого ребра не має, закінчити процедуру, тобто вихідний граф не містить остовного дерева). Після вказаного вибору можливі такі випадки:
а) якщо обидві вершини кінцевого вибраного ребра належать одному і тому ж букетові, то розфарбувати вибране ребро в зелений колір (воно не включається в дерево) і повернутись на початок кроку 2;
б) якщо одна з кінцевих вершин вибраного ребра належить деякому букетові, а інша кінцева вершина не належить ні одному із вже сформованих букетів, то розфарбувати вибране ребро в блакитний колір (воно включається в дерево) і включити його кінцеву вершину, яка не належала раніше ні одному з букетів у букет, якому належить інша кінцева вершина даного ребра;
в) якщо ні одна з кінцевих вершин не належить ні одному із сформованих букетів, то розфарбувати вибране ребро в блакитний колір і сформувати новий букет з його кінцевих вершин;
г) якщо кінцеві вершини вибраного ребра належать різним букетам, то розфарбувати ребро в блакитний колір, а обидва букети, яким належать його кінцеві вершини злити в один букет.
Після закінчення кроку 2 перейти до кроку 3.
Крок 3. Якщо всі вершини графу ввійшли в один букет, то закінчити процедуру, оскільки за цієї умови блакитні ребра утворюють остовне дерево.
В іншому випадку повернутись до кроку 2.
Зауважимо, що описаний алгоритм складається з багаторазового повторення кроку 2, причому, з кожним виконанням цього кроку деяке ребро розфарбовується в певний колір і залишається розфарбованим протягом всієї процедури. Тому, якщо вихідний граф складається із скінченої кількості ребер, алгоритм повинен закінчитися через скінчену кількість кроків.
Якщо алгоритм не закінчується побудовою остовного дерева, то вихідний граф взагалі не містить ні одного остовного дерева. Це зумовлене тим, що закінчення роботи алгоритму будуть сформовані в крайньому випадку два букети, для яких не знайдеться ні одного ребра, яке з’єднує будь-яку вершину одного ребра з них із будь – якою іншою. Дійсно, якщо б таке ребро знайшлося, воно під час роботи алгоритму було б розфарбовано в блакитний колір, і відповідні букети злилися би в один букет. Отже, алгоритм дає власне те, для чого він призначений: будує для графу остовне дерево (за умови, що граф містить таке дерево).
Приклад. Побудуємо покривальне дерево для графу, зображеного на мал. 2.
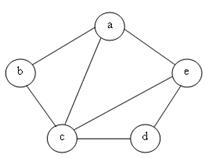
| В цьому графі: V = {a, b, c, d, e} - вершини E = {(a,b), (a,c), (a,e), (b,c), (c,d), (c,e), (d,e)} – ребра. аd-ланцюги: abcd, acd, aed. Дерева: aec, cba cbac– не є деревом, оскільки містить цикл |
Будемо розглядати ребра графу в такому порядку: {a, b}, {d, e}, {a, d}, {b, e}, {e, c}, {c, b}, {a, c} і {c, d}.

| Ребро | Колір | Букет №1 | Букет №2 |
| спочатку порожній | спочатку порожній | ||
| (a, b) | блакитний | a, b | порожній |
| (d, e) | блакитний | a, b | d, e |
| (a, d) | блакитний | a, b, d, e | порожній |
| (b, e) | зелений | a, b, d, e | порожній |
| (e, c) | блакитний | a, b, d, e, c | порожній |
Результати виконання кожного кроку алгоритму наведені вище. Алгоритм закінчується переглядом ребра (е, с), оскільки після цього вершини графу, що розглядаються, потрапляють в один букет. Чотири ребра (a,b), (d,e), (a,d), (a,c) утворюють для даного графу покриваюче дерево.
Переваги даного алгоритму такі:
- володіє властивістю, яка полягає в тому, що кожне ребро проглядається не більше одного разу;
- якщо під час виконання алгоритму деяке ребро розфарбувалося, то це ребро надалі не можна проглянути ще раз.
Це впливає нате, що:
- під час роботи не потрібно використовувати час на повторний перегляд відповідних елементів;
- для цих алгоритмів достатньо просто визначити кількість операцій, що використовується.
Тепер розглянемо задачу пошуку остовного дерева з мінімально або максимально можливою вагою, яка називається відповідно задачею про мінімальне або максимальне остовне дерево. Очевидно, якщо граф містить деяке остовне дерево, то в ньому можна виділити як мінімальне, так і максимальне остовне дерево. Ці остовні дерева можна легко побудувати за допомогою розглянутого вище алгоритму, вибираючи відповідно порядок перегляду ребер.
Алгоритм побудови мінімального остовного дерева – це побудова остовного дерева, в якому ребра проглядають в порядку зростання їх ваг (перше ребро – з мінімальною вагою, останнє – з максимальною вагою). Якщо два і більше ребра мають однакову вагу, то вони впорядковуються довільно.
Алгоритм побудови максимального остовного дерева – це побудова остовного дерева, в якому ребра проглядають в порядку спадання їх ваг (перше ребро – з максимальною вагою, останнє – з мінімальною вагою). Якщо два і більше ребер мають однакову вагу, то вони впорядковуються довільно.
Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ
з дисципліни «Інформатика інфокомунікаційних систем, ч. 2»
для студентів базового напряму 050902 «Радіоелектронні апарати»,
які навчаються заочно за скороченим терміном підготовки
в Інституті післядипломної освіти
(освітньо – кваліфікаційний рівень: бакалавр)
Укладачі І.В. Атаманова, канд. техн. наук, доц.
Редактор






