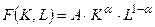Прежде всего, исследуем вопрос о свойствах траекторий модели в стационарном режиме, когда относительные показатели не изменяются во времени. На стационарной траектории 
. Из дифференциального уравнения следует, что существует два стационарных режима: нулевой и 
.
Благодаря условиям, наложенным на производственную функцию, 
конечно и положительно, а стационарное состояние устойчиво, так как 
при 
, 
при 
. Таким образом, если в начальный момент времени 
, то k (t) возрастает, иначе – убывает. При этом в первом случае график функции k (t) имеет точку перегиба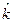 
, в которой обращается в ноль вторая производная функции k (t) (а значит, производная по k от правой части уравнения). При 
график функции является выпуклым вниз, при 
- выпуклым вверх.
Если k (t) = k *, то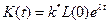 
. С тем же темпом растут Y (t), C (t) и I (t). Такую ситуацию называют режимом сбалансированного роста. Режим сбалансированного роста обладает тем свойством, что к нему сходятся все траектории модели при постоянной доле капиталовложений. Режим сбалансированного роста сам зависит от нормы капиталовложений s, так как от s зависит значение k*: при росте s величина k* возрастает. Поскольку все траектории сходятся к сбалансированному росту, который зависит от величины постоянной доли капиталовложений s, то возникает вопрос о том, какой режим сбалансированного роста предпочтительнее. Для этого прежде всего необходимо ввести критерий, по которому мы будем сравнивать различные режимы. В модели сбалансированного роста в качестве критерия можно взять уровень потребления в расчете на одного трудящегося, т. е. величину c = (1− s) f (k*), причем k* также зависит от величины s, и в итоге c (s) = f (k*) − (λ + μ) k*, где k*=k* (s). Условие экстремума этой функции во внутренней точке отрезка [0,1], к которому принадлежат допустимые значения s, выписывается в виде d c (s)/d s =0 или (f '(k*) − (λ+ μ))d k* /d s = 0, и т.к. d k* /d s >0, то f '(k*)= (λ + μ). Заметим, что в случае рассматриваемых производственных функций всегда существует единственное решение k*, удовлетворяющее этому уравнению. Наилучшее значение доли капиталовложений в конечном продукте s можно определить из соотношения s * = (λ + μ) k */ f (k*). Легко проверить, что полученное значение s приведет к максимальному, а не минимальному потреблению, а также то, что максимальное потребление не достигается при крайних значениях величины s, т. е. при s =0 или s =1. Для расчета оптимальной нормы накопления нужно задать конкретную производственную функцию. Например, для функции Кобба-Дугласа получаем s *= α, то есть оптимальная норма накопления совпадает с ее эластичностью («Золотое правило накопления»).
Задания к лабораторной работе 8
Пусть в модели Солоу темп прироста трудовых ресурсов λ, предельная склонность к сбережению s и коэффициент μ заданы в %.
1. Найти стационарное значение фондовооруженности.
2. Вычислить 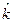- значение фондовооруженности, при котором скорости роста функци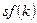й 
и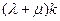 
равны.
3. Исследовать переходные режимы в модели. Убедиться, что в зависимости от соотношения значений 
, 
, 
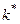наблюдается: ускоренный вначале рост фондовооруженности; замедленный рост фондовооруженности; замедляющееся падение фондовооруженности.
4. Пусть момент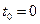 
значения 
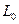и 
заданы. В каком направлении будет изменяться темп прироста 
в соответствии уравнением модели? Какой начальный объем капитала при заданном 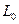обеспечит равновесный рост? Какой начальный объем капитала при заданном 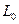обеспечит убывание (возрастание) фондовооруженности?
5. Найти оптимальное значение s*. Построить графики решения уравнения 
с заданными значениями параметров и заданным начальным условием при s =5;15;20;30;40;50;60;75;80 (величина задана в процентах). Убедиться, что уровень потребления в расчете на одного трудящегося, т. е. величина c = (1− s) f (k*), максимальна при s=s* (то есть золотое правило накопления действительно выполняется).
В качестве производственной функции взять:
| Показатель | Номер варианта | |||||
| 1-3 | 4-6 | 7-9 | 10-12 | 13-15 | 16-18 | |
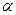
| 0.2+0.1 n, где n – остаток от деления номера варианта на 4 | |||||
| A | 1.1+0.1 n, где n – остаток от деления номера варианта на 4 | |||||
| ||||||
| ||||||
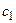
| a | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| b | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
 (%)
| 2.0 | 2.2 | 2.4 | 2.6 | 2.8 | 3.0 |
| s (%) | ||||||
 (%)
| ||||||
|
| ||||||
|
|
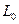
Список литературы
1. Электронный курс по прикладному математическому пакету MathCAD2001 (Pro) http://detc.ls.urfu.ru/assets/amath0021/
2. С. В. Алябьева, Е. П. Борматова, М. В. Данилова, Е. Е. Семѐнова. MathCAD для студентов: Учебный практикум. Изд-во ПетрГУ. – Петрозаводск, 2007. http://petrsu.ru/Deps/MMSU/Mcad_uchebnik.pdf
