Задание № 1. Используя операцию Символы ® Расчеты ® С плавающей запятой…, представьте:
1) число p в семи позициях;
2) число 12,345667 в трех позициях.
Задание № 2. Выведите следующие числа в комплексной форме, используя операцию Символы ® Расчеты ® Комплексные:
1) 
;
2) 
;
3) для выражения 2) последовательно выполните операции Расчеты ® Комплексные и Символы ® Упростить.
Задание № 3. Для полинома g(x) выполнить следующие действия:
1) разложить на множители, используя операцию Символы ® Фактор;
2) подставьте выражение x = y + z в g(x), используя операцию Символы ® Переменные ® Замена (предварительно скопировав подставляемое выражение в буфер обмена, выделив его и нажав комбинацию клавиш Ctrl + C);
3) используя операцию Символы ® Расширить, разложите по степеням выражение, полученное в 2);
4) используя операцию Символы ® Подобные, сверните выражение, полученное в 3), по переменной z.
| Вариант | g (x) | Вариант | g (x) |
| 1. | x 4 - 2 x3 + x 2 - 12 x + 20 | 2. | x 4 + x3 - 17 x 2 - 45 x - 100 |
| 3. | x 4 + 6 x3 + x 2 - 4 x - 60 | 4. | x 4 - 5 x3 + x 2 - 15 x + 50 |
| 5. | x 4 - 14 x 2 - 40 x - 75 | 6. | x 4 - 4 x3 - 2 x 2 - 20 x + 25 |
| 7. | x 4 - x3 + x 2 - 11 x + 10 | 8. | x 4 + 5 x3 + 7 x 2 + 7 x - 20 |
| 9. | x 4 - x3 - 29 x 2 - 71 x - 140 | 10. | x 4 - 7 x3 + 7 x 2 - 5 x + 100 |
| 11. | x 4 + 7 x3 + 9 x 2 + 13 x - 30 | 12. | x 4 + 10 x3 + 36 x 2 + 70 x + 75 |
| 13. | x 4 + 3 x3 - 23 x 2 - 55 x - 150 | 14. | x 4 + 9 x3 + 31 x 2 + 59 x + 60 |
| 15. | x 4 - 6 x3 + 4 x 2 + 10 x + 75 | 16. | 15 x4- 6 x3+ 4 x2 -12 x- 10 |
Задание № 4. Разложите выражения на элементарные дроби используя операцию Символы ® Переменные ® Конвертировать в частичные доли:
1)  ;
| 2)  ;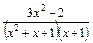
|
3)  ;
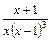| 4)  .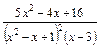
|
Задание № 5. Разложите выражения в ряд с заданной точностью, используя операцию Символы ® Переменные ® Разложить…:
1) ln (1 + x), х 0 = 0, порядок разложения 6;
2) sin (x)2, х 0 = 0, порядок разложения 6.
Задание № 6. Найти первообразную аналитически заданной функции f (x) используя команду Символы ® Переменные ® Интеграция.
Задание № 7. Определить символьное значение первой и второй производных f(x), используя командуСимволы ® Переменные ® Дифференциалы.
Варианты заданий № 6 и № 7
| Вариант | f (х) | Вариант | f (х) | Вариант | f (х) |
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
|
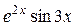
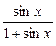
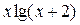
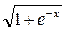
Задание № 8.
1. Транспонируйте матрицу М с помощью операции Символы ® Матрицы ® Транспонирование.
2. Инвертируйте матрицу 
с помощью операции Символы ® Матрицы ® Инвертирование.
3. Вычислите определитель матрицы 
с помощью операции Символы ® Матрицы ® Определитель.
Задание № 9. Вычислите пределы.
1. 
2. 
3. 
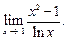4. 
Задание № 10.Найдите сумму ряда.
1. 
. 2. 
Задание № 11. Найдите производную и упростите выражение.
1. 
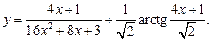
2. 
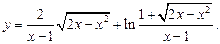
Задание № 12. Вычислите неопределенные интегралы.
1. 
2. 
Задание № 13.Вычислите определенные интегралы.
1. 
2. 
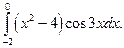
Лабораторная работа 6. Решение обыкновенных дифференциальных уравнений в MathCad
Общие сведения
Задачи анализа математических моделей в большинстве случаев связаны с решением дифференциальных уравнений и систем таких уравнений. Во многих случаях необходимо найти решения обыкновенных дифференциальных уравнений – функцию (или функции) от одного аргумента. При этом аналитическое решение дифференциального уравнения удается найти лишь в исключительных случаях. Однако современные системы компьютерной математики предоставляют широкие возможности численного решения дифференциальных уравнений. В этом случае результатом вычислений является конкретное решение (траектория, фазовая кривая) дифференциального уравнения, и для ее нахождения требуется, помимо уравнения, задать дополнительные условия – начальные или граничные. Характерной чертой численных методов является то, что и исходные данные, и результат имеют вид числа или набора чисел. Для дифференциального уравнения первого порядка решение представляется в виде набора чисел. Отрезок [ a, b ], на котором строится решение, разбивается на (равные или нет) промежутки: 
. Полученное разбиение называется сеткой, точки 
называются узлами сетки. В этих узлах и определяются значения функции (или функций): 
, 
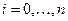. Таким образом, в результате вычислений получается решение в виде набора (или нескольких наборов, по числу искомых функций) чисел. Для получения представления о поведении этого решения обычно строится график функции на плоскости переменных 
. Если искомых функций несколько, можно нарисовать их графики на одной координатной плоскости. Если функций две или три, для наглядности используется также фазовая плоскость (фазовое пространство) – в этом случае независимая переменная становится параметром.
