Задания к лабораторной работе 7

Задание №1. Исследовать поведение системы Лотки-Вольтерра при различных значениях параметров:

 

№	Система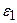
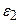
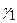
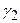
	Амурский тигр – кабан	0,72	0,15	0,0125	0,009
	Волк – заяц	0,8	0,45	0,014	0,005
	Щука – карась	0,5	0,45	0,02	0,002
	Лиса – мышь	0,75	0, 25	0,0115	0,006
	Сова – мышь	1,20	0,35	0,02	0,0001
	Лев – антилопа гну	0,60	0,25	0,025	0,00001
	Стрекоза – комар	20,0	2,0	0,05	0,02
	Крокодил – зебра	0,50	0,05	0,022	0,00001
	Рысь – заяц	0,66	0,2	0,02	0,0003
	Тигр – изюбрь	0,82	0,45	0,024	0,005
	Волк – косуля	0,8	0,45	0,02	0,005
	Нерпа – лосось	0,55	0, 25	0,05	0,006
	Беркут – бурундук	0,55	0,25	0,015	0,005
	Еж – змеи	1,20	0,55	0,02	0,0001
	Цапля – лягушка	0,85	0,30	0,0115	0,005
	Кукушка – стрекоза	20,0	2,0	0,05	0,02

 

Решить систему дифференциальных уравнений с различными начальными условиями. В частности, в качестве начальных условий взять , , 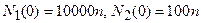(здесь n – номер варианта).

Нарисовать графики функций 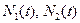на промежутках [0,10] и [0,100]. Проанализировать зависимость изменения численностей от соотношения начальных значений.

Задание №2. Найти координаты точки равновесия системы Лотки-Вольтерра при заданных в задании №1 значениях параметров. Нарисовать фазовые кривые системы с заданными параметрами и различными начальными условиями, в том числе в качестве начального условия взять координаты точки равновесия. Сравнить результат с приведенным рисунком. Нарисовать на плоскости линии 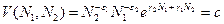для различных значений c >0.

На основании расчётов и полученных графических зависимостей сделайте выводы, оценив:

– поведение системы при различных параметрах, а также при различных начальных условиях;

– периоды колебаний численности «хищников» и «жертв»;

– при каких отклонениях от стационарных значений численности гармонические колебания сменяются сложными колебаниями, а форма фазовой траектории перестаёт быть эллипсом.

 

Лабораторная работа 8. ИССЛЕДОВАНИЕ МОДЕЛи солоу

Общие сведения

Вычислительный эксперимент является важнейшим этапом современного математического моделирования. Во многих случаях описание модели или ее части сводится к обыкновенным дифференциальным уравнениям, найти точное аналитическое решение которых не представляется возможным. В этом случае исследование модели представляет собой применение качественных и численных методов анализа. При этом в сочетании с теоретическими исследованиями численные методы позволяют приближенно находить не только конкретные (частные) решения, но и глобальные характеристики системы. Предварительный качественный анализ модели позволяет получить предварительную информацию о характере поведения решений системы и возможных вариантах этого поведения, о наличии особых траекторий и (или) особых значений параметров систем, что, в свою очередь, помогает правильно выбрать способ и параметры численного решения дифференциальных уравнений модели. Чем сложнее система, тем более важную роль для успеха вычислительного эксперимента играет предварительное аналитическое исследование модели.

Рассмотрим однопродуктовую (односекторную) модель, характеризующуюся в каждый момент времени набором переменных: Y – валовой выпуск, С – непроизводственное потребление, I – инвестиции, L – трудовые ресурсы (число занятых), К – производственные фонды (капитал), λ – темп роста трудовых ресурсов, μ – коэффициент выбытия ПФ. В такой модели продукция экономики считается однородной, т.е. состоящей из одного продукта. Все предприятия рассматриваются нераздельно, объединены в одну производственную единицу (отсюда и второе название модели – односекторная). Предполагается, что выпуск в каждый момент времени определяется производственной функцией Y = F (K,L).

Выпишем основные балансовые соотношения модели в удельных (душевых) переменных:

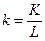- фондовооруженность, 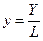- удельный выпуск (производительность труда), 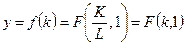, , 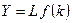. (1.10)

В силу свойств производственной функции

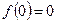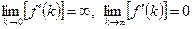, . (1.11)

Балансовое условие агрегированной экономики: .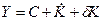

Основные предположения модели:

1. модель динамики трудовых ресурсов описывается уравнением (мальтузианский рост);

2. модель воспроизводства основных производственных фондов описывается уравнением 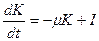, где – норма выбытия ОПФ, 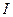– инвестиции.

3. население сберегает (и инвестирует) постоянную долю своего дохода .

С учетом основного макроэкономического тождества 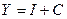получаем в абсолютных показателях 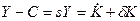, откуда с учетом введенных обозначений выводим основное уравнение модели: .