Систему дифференциальных уравнений можно решить, используя тот же блок Given/odesolve. При этом количество начальных условий равно сумме порядков всех уравнений, входящих в систему.
Задания к лабораторной работе 6
Задание №1.
Найти решение задачи Коши для обыкновенного дифференциального уравнения с использованием «блока решений» и с использованием встроенной функции rkfixed. Сравнить графики полученных решений.
| Номер варианта | Правая часть уравнения f (x, y) | Начальные условия | Интервал нахождения решения | Шаг изменения |
| y(1)=1 | [1,10] | ||
| tg(x)tg(y) | y(0)=0 | [0,5] | 0.5 | |
| y(1)=1 | [1,7] | ||
| y(1)=1 | [1, 5] | 0.25 | |
| cos(x -2 y)-cos(x +2 y) | y(0)=p/4 | [0,4p] | p/2 | |
| y(0)=0 | [0;3,5] | 0,1 | |
| y(0)=0 | [0;1] | 0,05 | |
| lnôx+2,5xsin(x)ô | y(0)=2,5 | [1;3,5] | 0,2 | |
| y(0)=0 | [0;1,5] | 0,1 | |
| y(0)=3,5 | [1,2;2,4] | 0,08 | |
| y(0)=3,6 | [4,1;6,7] | 0,1 | |
| y(0)=2,2 | [0,8;3,2] | 0,1 | |
| y(0)=16,2 | [4,8;6,4] | 0,1 | |
| 0,7y+x×ln(x+y) | y(0)=2,5 | [12,4;14,1] | 0,08 |
| y(0)=3,1 | [8,5;9,7  ]
| 0,05 | |
| y(0)=1,4 | [0;2,3] | 0,1 | |
| y(0)=1,7 | [2,4;3,5] | 0,05 | |
| y(0)=2,8 | [1,6;3,1] | 0,1 | |
| y(0)=5,7 | [14,5;16,3] | 0,05 | |
| y(0)=1,6 | [5,2;6,8] | 0,1 | |
| y/ln(y) | y(2)=1 | [2;5] | 0,25 | |
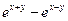
| y(0)=0 | [0;2.5] | 0,1 | |
| y(p/4)=0 | [p/4, 3p] | p/8 | |
| y(1)=0 | [1;4] | 0.3 | |
| sin(3x)-y×tg(3x) | y(0)=1/3 | [0,4] | 0,25 | |
| cos(x-4y)-cos(x+4y) | y(0)=p/4 | [0,4p] | p/2 | |
| y(0)=0 | [0;3,5] | 0,1 | |
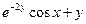
| y(0)=0 | [0;1] | 0,05 | |
| lnôx+sin(x)ô | y(0)=2,5 | [1,5;3,5] | 0,2 | |
| y(0)=0 | [0;1,5] | 0,1 |
Задание №2. Найти численное решение задачи Коши для системы дифференциальных уравнений согласно номерам задачника Филиппова. Использовать начальные условия x(0)=0; y(0)=1.
В1. №826
В2. №827
В3. №828
В4. №829
В5. №830
В6. №831
В7. №832
В8. №833
В9. №834
В10. №835
В11. №836
В12. №837
В13. №838
В14. №839
В15. №840
Контрольные вопросы
1. Какие встроенные функции позволяют найти решение обыкновенных дифференциальных уравнений?
2. Нужно ли обязательно задавать начальные условия для решения обычных дифференциальных уравнений?
3. Как влияет на результат количество точек разбивки интервала интегрирования обыкновенных дифференциальных уравнений?
Лабораторная работа 7. ИССЛЕДОВАНИЕ МОДЕЛи лотки-вольтерра
Общие сведения
Вычислительный эксперимент является важнейшим этапом современного математического моделирования. Во многих случаях описание модели или ее части сводится к обыкновенным дифференциальным уравнениям, найти точное аналитическое решение которых не представляется возможным. В этом случае исследование модели представляет собой применение качественных и численных методов анализа. При этом в сочетании с теоретическими исследованиями численные методы позволяют приближенно находить не только конкретные (частные) решения, но и глобальные характеристики системы. Предварительный качественный анализ модели позволяет получить предварительную информацию о характере поведения решений системы и возможных вариантах этого поведения, о наличии особых траекторий и (или) особых значений параметров систем, что, в свою очередь, помогает правильно выбрать способ и параметры численного решения дифференциальных уравнений модели. Чем сложнее система, тем более важную роль для успеха вычислительного эксперимента играет предварительное аналитическое исследование модели.
Модель Лотки-Вольтерра
Взаимоотношения хищник – жертва – это те взаимоотношения, представления о динамике которых разработаны наиболее глубоко. Еще в первой половине XX века вышли две основополагающие работы – А. Лотки (1925) и В. Вольтерра (1931), в которых авторы независимо друг от друга сформулировали аналитическую модель, описывающую динамику этих взаимоотношений, точнее – динамику численности популяции хищника и динамику численности популяции жертвы.
Как обычно и бывает в моделях, ситуация, описываемая моделью Лотки – Вольтерра, – это ситуация идеализированная, упрощенная. Поскольку нас интересует только взаимоотношения между данной популяцией хищника и данной популяцией жертвы, мы пренебрегаем тем, что хищник может питаться не только данным видом или данной популяцией жертвы, равно как и тем, что популяцию жертвы может выедать не только «наш» хищник, но и другие. Мы пренебрежем также и тем, что на численность популяции жертвы может оказывать влияние доступность для нее кормового ресурса, а на численность обеих популяций – прочие ограничивающие факторы, включая внутривидовую конкуренцию внутри популяции хищника и внутри популяции жертвы.
Если N1 – численность жертвы, а N2 – численность хищника, то общее изменение численности популяции жертв за единицу времени будет складываться из двух составляющих – прироста за счет рождаемости и убыли за счет выедания. Итоговая формула:
Предполагая теперь, что в отсутствие жертв хищники вымирают по экспоненциальному закону, получаем, общее изменение численности популяции хищника будет описываться формулой: 
. Здесь знаки выбраны так, что значения всех параметров положительны.
В итоге получаем систему двух дифференциальных уравнений:
Как будут соотноситься численности популяций хищника и жертвы в такой системе? Очевидно, что в принципе возможно ожидать реализацию одного из трех сценариев. Сценарий 1: невзирая на давление хищника, популяция жертвы продолжает наращивать численность. В нашей замкнутой модельной системе такой рост может быть безграничным. Сценарий 2: хищники выедают всю популяцию жертвы. Такой сценарий катастрофичен для обеих популяций даже в рамках нашей замкнутой модели, поскольку сначала от хищников гибнет вся популяция жертв, а затем, оставшись без пищи, неминуемо гибнет и популяция хищников. Наконец, сценарий 3 означает, что между численностью хищников и жертв должно возникнуть некое равновесие.
При каких условиях в системе Лотки – Вольтерра возникает равновесная ситуация?
Равновесие означает, что численность популяции жертвы не меняется, то есть число отродившихся особей равно числу съеденных. Иными словами, за счет этого баланса популяция жертвы испытывает нулевой прирост. На языке математики этот нулевой прирост будет выглядеть так: 
то есть 
, и аналогично 
.
Очевидно, в рамках модели Лотки-Вольтерра, что если численность жертв меньше равновесной, численность хищников будет уменьшаться, а если численность жертв больше равновесной, численность хищников будет возрастать. В то же время, с численностью жертв будет наблюдаться обратная картина: если численность хищников меньше равновесной, численность жертв будет возрастать, а если численность хищников больше равновесной, численность жертв будет уменьшаться.
Можно показать, что функция 
является общим интегралом системы, то есть линии ее уровня представляют собой замкнутые траектории системы, содержащие внутри себя точку равновесия:
Таким образом, модель описывает периодические незатухающие колебания численности и хищника и жертвы.
