Пусть имеем определитель n -го порядка. Его вычисление вполне определяется приводимыми ниже теоремами.
Теорема 1: Произведение любого минора Мk -го порядка на его алгебраическое дополнение АМ в определителе d есть сумма некоторых членов определителя с теми же знаками, с какими они входят в состав определителя.
Теорема 2 (Лапласа) Пусть в определителе d порядка n произвольно выбраны k строк (или столбцов) 
. Тогда сумма произведений всех миноров k -го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.
Частным случаем теоремы Лапласа является разложение определителя d:
по i -й строке:
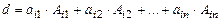(56)
по j -му столбцу:
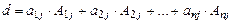(57)
Учитывая свойство 4 определителей запишем также:
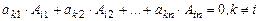(58)
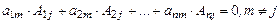(59)
☺ Пример 41. Определим знак члена определителя, определяемого записью:
,
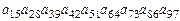Решение: Составим подстановку так, что первый индекс помещается в первую строку подстановки, а второй – во вторую ее строку, и разложим подстановку в произведение циклов:
.
Определим декремент: для записанной подстановки: d = n = 9 – 3 = 6, где 9 – порядок подстановки, 3 – число циклов в разложении подстановки → подстановка четная. Следовательно, заданный член определителя учитывается в записи суммы членов определителя со знаком «+».
Ответ: Положительный.
Пример 42. Определим знак члена определителя, определяемого записью:.
, (*)
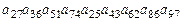Решение: Составим подстановку так, что первый индекс помещается в первую строку подстановки, а второй – во вторую ее строку, и разложим подстановку в произведение циклов:
.
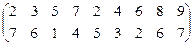Так как в верхней строке дважды используется элемент «2» и ни разу «1», то запись (*) не является членом определителя
Ответ: Исходная запись не является членом определителя.
Пример 43. Докажем тождество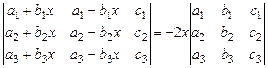 
,
используя свойства определителя.
Решение: Обозначим левую часть тождества dL и произведем цепочку последовательных преобразований: 1-й шаг: 2С +1С; 2-й шаг: а) меняем местами 1-й и 2-й столбцы; б) выносим за скобку определителя общий множитель столбца (см. множитель “-2”); 3-й шаг: 2С - 1С; 4-й шаг: выносим за скобку общий множитель x: тождество доказано.
| 1 шаг | a1+b1x | 2a1 | c1 | 2 шаг | a1 | a1+b1x | c1 | 3 шаг | a1 | b1x | c1 | 4 шаг | a1 | b1 | c1 |
| dL= | a2+b2x | 2a2 | c2 | =–2 | a2 | a2+b2x | c2 | = –2 | a2 | b2x | c2 | = –2x | a2 | b2 | c2 |
| a3+b3x | 2a3 | c3 | a3 | a3+b3x | c3 | a3 | b3x | c3 | a3 | b3 | c3 |
Ответ: см. схему преобразований доказательства.
Пример 43. Вычислим определитель 4-го порядка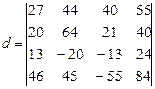 
,
используя свойства определителя n – го для упрощения вычислений.
Решение: Вычислим определитель, применяя цепочку преобразований: 1-й шаг: 4С-1Сх2; 1R-2R; 2-й шаг: 4R-3Rх4; 3-й шаг: разложение определителя по 4-му столбцу; 4-й шаг: 3С-1С; 5 -й шаг: 3R+2R;2R+1R; 6 -й шаг: 3R-1R;2R+1R; 7-й шаг: разложение определителя по 3-му столбцу и вычисление определителя 2-го порядка:
| 1 шаг | 7 | -20 | 19 | 1 | 2 шаг | -20 | 3 шаг | 20 | 64 | 21 | 4 шаг | 20 | 64 | 1 | |||
| 20 | 64 | 21 | 0 | = | 20 | 64 | 21 | =1(-1)1+4 | 27 | -60 | 25 | = (-1)∙ | 27 | -60 | -2 | ||
| dL= | 13 | -20 | -13 | -2 | 27 | -60 | 25 | -6 | 125 | -3 | -6 | 125 | 3 | ||||
| 46 | 45 | -55 | -8 | -6 | 125 | -3 |
| 5 шаг | 20 | 64 | 1 | 6 шаг | 20 | 64 | 1 | 7 шаг | 67 | 68 | |
| = (-1)∙ | 47 | 4 | -1 | = (-1)∙ | 67 | 68 | 0 | =1∙(-1)∙(-1)1+3 | 1 | 1 | = 1 |
| 21 | 65 | 1 | 1 | 1 | 0 |
Ответ: 1.
Пример 44. Вычислим определитель 5-го порядка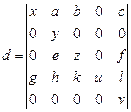 
,
используя разложения «по строке» или «по столбцу»:
Решение: Учитывая правила разложения определителя по строке и по столбцу, запишем цепочку последовательных преобразований::
| x | a | b | 0 | c | x | a | b | |||||||
| 0 | y | 0 | 0 | 0 | y | 0 | x | a | b | |||||
| 0 | e | z | 0 | f | =v (-1)5+5 | 0 | e | z | = vu (-1)4+4 | y | = xyzuv | |||
| g | h | k | u | l | g | h | k | u | e | z | ||||
| v |
Ответ: x ∙ y ∙ z ∙ u ∙ v.
Пример 45. Вычислим определитель 6-го порядка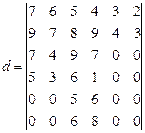 
,
используя разложения «по k строкам» или «по k столбцам» (см. теорему Лапласа).
Решение: В рассматриваемом примере первый шаг вычислений подсказан тем, что в 5-м и 6-м столбцах только один определитель 2-го порядка не равен нулю. Значит выгодно разложение по этим двум столбцам. Учитывая правила разложения определителя «по k столбцам», запишем цепочку последовательных преобразований::
| 3 | 2 | |||||||||||||||||||
| = | 4 | 3 | ∙(-1)1+2+5+6 | = | ∙(-1)1+2+5+6∙ | = 4 | ||||||||||||||
Ответ 4.
☻ Решите примеры:
Пример 46. Вычислите определитель: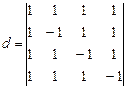 
.
Ответ -8.
Пример 47. Вычислите определитель: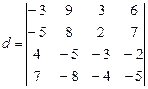 
.
Ответ 18.
Пример 48. Вычислите определитель: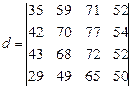 
.
Ответ 10.
Пример 49. Вычислите определитель: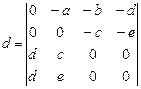 
.
Ответ (be – cd)2.
Вопросы для самопроверки:
1. Может ли определитель n -го порядка не быть числом?
2. Изменится ли определитель n -го порядка, если в нем строки заменить столб-цами и наоборот?
3. Изменится ли определитель n -го порядка, если в нем строки (или столбцы) поменять местами?
4. Изменится ли определитель n -го порядка, если в нем из одной строки вычесть другую строку?
5. Изменится ли определитель n -го порядка, если в нем из одного столбца вычесть другой столбец?
6. Изменится ли определитель n -го порядка, если в нем строку умножить на число 2?
7. Применение теоремы Лапласа предполагает уменьшение трудоемкости вычисления определителей высокого порядка?
8. Может ли произведение нескольких невырожденных квадратных матриц n -го порядка дать в результате вырожденную матрицу?
