Пусть имеем квадратную матрицу третьего порядка:
A = 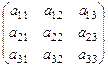 , (12)
, (12)
элементами aij, которой могут быть элементы любого числового поля.
Определителем третьего порядка называется число:
a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - a 13 a 22 a 31 - a 12 a 21 a 33 - a 11 a 23 a 32 , (13)
составленное из элементов матрицы A. Слагаемые суммы (13) называют членами определителя 3-го порядка. Обозначения определителя 3-го порядка аналогичны введенным для определителя 2-го порядка:
 (14)
(14)
Для запоминания формулы (13) нередко используют геометрическую схему составления членов определителя и выбора их знаков.
1) положительные члены определителя составляют по схеме С1:
| a11 | a12 | a13 | ||||||||
| a22 | a23 | a21 | ||||||||
| a33 | a31 | a32 |
2) отрицательные члены определителя составляют по схеме С2:
| a13 | a12 | a11 | ||||||||
| a22 | a21 | a23 | ||||||||
| a31 | a33 | a32 |
Для рассмотрения общего случая определителей n -го порядка установим основные свойства определителей 3-го порядка (все они справедливы и для определителей 2-го порядка).
Свойство 1. Величина определителя не изменится, если строки и столбцы этого определителя поменять ролями (для матрицы это преобразование называется транспонированием матрицы):
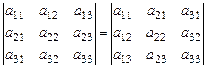 (15)
(15)
Доказательство этого свойства легко наблюдается на схемах С1 и С2: члены определителя составляются из элементов, взятых по одному из каждой строки и каждого столбца (причем ни один элемент не пропущен), как до транспонирования, так и после него. Сохранение знаков членов также очевидно.
Свойство 1 устанавливает полную равноправность строк и столбцов. Это значит, что в дальнейшем все свойства можно формулировать и для строк, и столбцов, но доказывать только для строк (или только для столбцов).
Свойство 2. Перестановка двух строк (или столбцов) определителя равносильна умножению его на число –1.
Доказательство достаточно легко пронаблюдать по схемам С1 и С2. Допустим поменяли местами строки 2-ю и 3-ю. Это приводит к перемещению всех трех «клеток» из схемы С1 формирования положительных членов определителя в схему С2 для формирования отрицательных членов, и наоборот.
Свойство 3. Если определитель имеет две одинаковые строки (или два одинаковых столбца), то он равен нулю.
Действительно, при перестановке двух одинаковых строк определитель не меняется, а по свойству 2 должен поменять знак на противоположный. Это значит, что d = -d, или d = 0.
Свойство 4. Умножение всех элементов некоторой строки (или столбца) определителя на число λ равносильно умножению определителя на это число.
Это значит, что общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак этого определителя:
 (16)
(16)
Это следует из выражения (13), а также из схем С1 и С2 формирования каждого члена определителя: каждый член определителя содержит только один элемент (причем обязательно содержит) из каждого столбца определителя.
Свойство 5. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю.
Это свойство вытекает из свойства 4 при λ = 0.
Свойство 6. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю.
Это следует из последовательного применения свойства 4 (вынесение коэффициента пропорциональности за знак определителя) и свойства 3 (в определителе оказалось две равные строки).
Свойство 7. Если каждый элемент n-й строки (или n-го столбца) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей:
 (17)
(17)
Это следует из выражения (13) и правила формирования каждого члена определителя: каждый член определителя содержит только один элемент (причем обязательно содержит) из каждого столбца определителя, а также из распределительного свойства операций умножения и сложения для элементов числового поля.
Свойство 8. Если к элементам некоторой строки (или столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умножен-ные на произвольный множитель λ, то величина определителя не изменится.
Это следует из последовательного применения свойства 7 (разбить определитель на сумму двух определителей) и свойства 6 (второй определитель равен нулю, т.к. имеет две пропорциональные строки (два пропорциональных столбца)).
Для рассмотрения «Свойства 9» требуется предварительно определить понятия «Минор данного элемента» и «Алгебраическое дополнение данного элемента».определи-теля 3-го порядка.
Преобразуем запись (13) определителя:
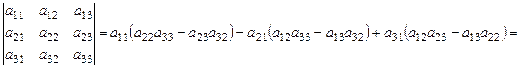

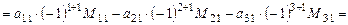
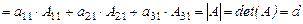 (18)
(18)
В соответствии с (17) определим:
1) Mij – минор элемента aij: получается из данного определителя вычеркиванием строки i и столбца j, на пересечении которых стоит элемент aij;
2) Aij – равняется минору элемента aij, взятому со знаком (+), если сумма i+j есть число четное, и со знаком (-) – в противном случае.
Запись (18) значит, что определитель равен сумме произведений элементов какого-либо столбца (какой-либо строки) на соответствующие алгебраические дополнения элементов этого столбца (строки):
 (19)
(19)
 (20)
(20)
Воспользуемся записью (18) и заменим 1-й столбец произвольными числами h 1, h 2, h 3:
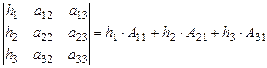 . (21)
. (21)
Если вместо чисел h 1, h 2, h 3 взять элементы 2-го или 3-го столбцов определителя, получим (см. свойство 3):
 (22)
(22)
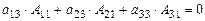 (23)
(23)
Учитывая полученные результаты, определим еще одно важнейшее свойство определителя:
Свойство 9: определитель равен сумме произведений элементов какого-либо столбца (какой-либо строки) на соответствующие алгебраические дополнения элементов этого столбца (строки); определитель равен нулю, если взята сумма произведений элементов одного столбца (строки), а алгебраические дополнения составлены для элементов другого столбца (строки).
Рассмотрим некоторые приложения определителя 3-го порядка.
Пусть имеем систему уравнений с тремя неизвестными:
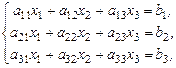 (24)
(24)
где коэффициенты a ij, 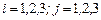 при неизвестных x i,
при неизвестных x i, 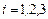 и свободные члены b i,
и свободные члены b i, 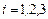 системы уравнений считаются заданными.
системы уравнений считаются заданными.
Системе уравнений (24) соответствуют: матрица системы A (составлена из коэффициентов при неизвестных) и расширенная матрица  (составлена из всех ее коэффи-циентов, включая свободные члены):
(составлена из всех ее коэффи-циентов, включая свободные члены):
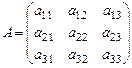 ,
, 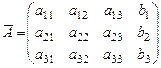 (25)
(25)
Умножим 1-е уравнение системы (24) на алгебраическое дополнение А 11, 2-е на А 21, 3-е на А 31 и сложим полученные уравнения:

 ,
,
или (см. свойство 9):
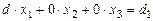 →
→  (26)
(26)
аналогично получим:
 ,
, 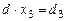 ,
,
причем, в выражениях (26):
 ,
,  ,
,  ,
, 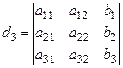
А. Если  , то для записи решения системы (3) можно использовать формулы Крамера:
, то для записи решения системы (3) можно использовать формулы Крамера:
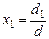 ,
,  ,
,  (27)
(27)
Формулы (27) определяют единственное решение. Если считать каждое уравнение системы (24) уравнением плоскости, то геометрический аналог рассматриваемой системы уравнений - совокупность трех пересекающихся в одной точке плоскостей α 1, α 2, α 3, причем точка пересечения плоскостей определяется решением (x 1, x 2, x 3). Линии пересечения пар плоскостей проходят через одну точку: X= (x 1, x 2, x 3).
Пусть уравнение плоскости имеет вид:
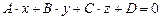 (28)
(28)
Известно, что вектор нормали к плоскости (28) определяется записью:
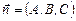 (29)
(29)
Тогда плоскостям α 1, α 2, α 3 соответствуют векторы нормалей:
 ,
, 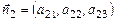 ,
, 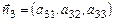 (30)
(30)
Б. Если  , то применение формул Крамера невозможно, и дальнейшее исследование системы уравнений (24) требует рассмотрения ряда случаев.
, то применение формул Крамера невозможно, и дальнейшее исследование системы уравнений (24) требует рассмотрения ряда случаев.
Случай 1. Две (только две) строки матрицы системы А пропорциональны (потому имеем  ). Пусть это будут строки 1 и 2, и пусть коэффициент пропорциональности равен λ. Это значит, что плоскости α 1, α 2 параллельны, т.е. векторы нормалей этих плоскостей
). Пусть это будут строки 1 и 2, и пусть коэффициент пропорциональности равен λ. Это значит, что плоскости α 1, α 2 параллельны, т.е. векторы нормалей этих плоскостей 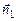 и
и 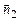 параллельны, т.е. коллинеарны:
параллельны, т.е. коллинеарны: 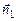 = λ
= λ 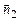 . В этом случае третья плоскость α 3 пересекает плоскости α 1, α 2 по прямым l 1, l 2, которые не пересекаются. Это значит, что система (24) решений не имеет. Это же следует из равенств (26): ни одно их них не может быть выполнено ни при каких значениях (x 1, x 2, x 3), т.к. ни один из определителей d 1, d 2, d 3 не равен нулю. Это значит, что система несовместна.
. В этом случае третья плоскость α 3 пересекает плоскости α 1, α 2 по прямым l 1, l 2, которые не пересекаются. Это значит, что система (24) решений не имеет. Это же следует из равенств (26): ни одно их них не может быть выполнено ни при каких значениях (x 1, x 2, x 3), т.к. ни один из определителей d 1, d 2, d 3 не равен нулю. Это значит, что система несовместна.
Случай 2. Все три строки матрицы системы А пропорциональны (потому имеем  ). Это значит, что плоскости α 1, α 2 и α 3 параллельны, т.е. векторы нормалей этих плоскостей
). Это значит, что плоскости α 1, α 2 и α 3 параллельны, т.е. векторы нормалей этих плоскостей 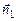 ,
, 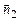 и
и  параллельны. В этом случае плоскости не пересекаются, т.е. не имеют общих точек. Это значит, что система (24) решений не имеет. Это же следует из равенств (26): ни одно их них не может быть выполнено ни при каких значениях (x 1, x 2, x 3), т.к. ни один из определителей d 1, d 2, d 3 не равен нулю. Это значит, что система несовместна.
параллельны. В этом случае плоскости не пересекаются, т.е. не имеют общих точек. Это значит, что система (24) решений не имеет. Это же следует из равенств (26): ни одно их них не может быть выполнено ни при каких значениях (x 1, x 2, x 3), т.к. ни один из определителей d 1, d 2, d 3 не равен нулю. Это значит, что система несовместна.
Замечание: в случаях 1 и 2 возможна ситуация, когда одновременно с равенством  выпол-няются равенства d 1=0, d 2=0 и d 3=0, причем последние равны нулю из-за равенства всех трех столбцов матрицы А. В таком случае параллельности соответствующих плоскостей остаются и точек, общих сразу для трех плоскостей, нет. Система уравнений (23) и в этом случае несовместна, хотя все равенства (26) выполняются для любых наборов чисел (x 1, x 2, x 3).
выпол-няются равенства d 1=0, d 2=0 и d 3=0, причем последние равны нулю из-за равенства всех трех столбцов матрицы А. В таком случае параллельности соответствующих плоскостей остаются и точек, общих сразу для трех плоскостей, нет. Система уравнений (23) и в этом случае несовместна, хотя все равенства (26) выполняются для любых наборов чисел (x 1, x 2, x 3).
Случай 3. Две (только две) строки расширенной матрицы  пропорциональны (потому имеем
пропорциональны (потому имеем  ). Пусть пропорциональны 2-я и 3-я строки. Это значит, что плоскости α 2, α 3 совпадают, а плоскость α 1 пересекает плоскости α 2, α 3 по прямой l 1-2, все точки которой являются общими для всех трех плоскостей. Решений (из геометрических соображений) должно быть бесчисленное множество.
). Пусть пропорциональны 2-я и 3-я строки. Это значит, что плоскости α 2, α 3 совпадают, а плоскость α 1 пересекает плоскости α 2, α 3 по прямой l 1-2, все точки которой являются общими для всех трех плоскостей. Решений (из геометрических соображений) должно быть бесчисленное множество.
На самом деле мы совпавшие плоскости не будем различать, т.к в рассматриваемом случае 3-е уравнение можно считать следствием 2-го и отбросить его. Далее необходимо рассматривать решение системы двух уравнений с тремя неизвестными:
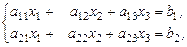 (31)
(31)
Т.к. строки системы уравнений (31) не пропорциональны (принято в рассматриваемом случае), то хотя бы один определитель системы (31):
 .
.
не равен нулю. Примем, что не равен нулю определитель:
 , (32)
, (32)
и запишем систему уравнений (31) в виде:
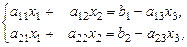 (33)
(33)
Далее, используя формулы Крамера (9) для случая  , присваивая произвольные значения переменной x 3, будем вычислять соответствующие значения x 1, x 2. Получаемые таким образом тройки чисел (x 1, x 2, x 3), будут принадлежать упоминаемой ранее линии l 1-2 пересечения плоскостей α 1, α 2. Следовательно исходная система (24) имеет бесчисленное множество решений и потому неопределенна.
, присваивая произвольные значения переменной x 3, будем вычислять соответствующие значения x 1, x 2. Получаемые таким образом тройки чисел (x 1, x 2, x 3), будут принадлежать упоминаемой ранее линии l 1-2 пересечения плоскостей α 1, α 2. Следовательно исходная система (24) имеет бесчисленное множество решений и потому неопределенна.
Случай 4. Все три строки расширенной матрицы  пропорциональны (потому имеем
пропорциональны (потому имеем  ). Это значит, что плоскости α 1, α 2 и α 3 совпадают и все точки одной из плоскостей принадлежат двум другим плоскостям.
). Это значит, что плоскости α 1, α 2 и α 3 совпадают и все точки одной из плоскостей принадлежат двум другим плоскостям.
На самом деле мы совпавшие плоскости не будем различать, т.к в рассматриваемом случае 2-е и 3-е уравнения можно считать следствием 1-го и отбросить их. Далее необходимо рассматривать решение одного уравнения с тремя неизвестными:
 (34)
(34)
Далее, присваивая произвольные значения переменным x 2, x 3, будем вычислять соответствующее значение x 1. Получаемые таким образом тройки чисел (x 1, x 2, x 3), будут принадлежать каждой из плоскостей α 1, α 2, α 3. Следовательно исходная система (24) имеет бесчисленное множество решений и потому неопределенна.
Представляет интерес рассмотреть частный случай системы уравнений с тремя неизвестными:
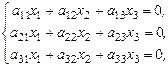 (35)
(35)
когда все свободные члены b i, 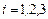 системы уравнений (24) равны нулю – одно-родная система уравнений.
системы уравнений (24) равны нулю – одно-родная система уравнений.
В этом случае каждое уравнение системы уравнений (35) соответствует плоскости, содержащей начало координат О (0, 0, 0). Это значит, что система уравнений (35) всегда имеет решение, т.к. плоскости α 1, α 2, α 3 имеют общую точку О.
Если  , то решение (0, 0, 0) – единственно. Геометрически это отвечает случаю, когда среди плоскостей α 1, α 2, α 3 нет параллельных (представление об этом случае дают координатные плоскости системы координат OXYZ, где линии пересечения пар плоскос-тей – это оси координат OX, OY, OZ).
, то решение (0, 0, 0) – единственно. Геометрически это отвечает случаю, когда среди плоскостей α 1, α 2, α 3 нет параллельных (представление об этом случае дают координатные плоскости системы координат OXYZ, где линии пересечения пар плоскос-тей – это оси координат OX, OY, OZ).
Если  , то две или все три плоскости α 1, α 2, α 3 совпадают. Тогда решение системы уравнений (33) – это либо множество точек линии пересечения (прямой) двух несовпавших плоскостей, либо все множество точек, принадлежащих одной плоскости (всем совпавшим плоскостям α 1, α 2, α 3).
, то две или все три плоскости α 1, α 2, α 3 совпадают. Тогда решение системы уравнений (33) – это либо множество точек линии пересечения (прямой) двух несовпавших плоскостей, либо все множество точек, принадлежащих одной плоскости (всем совпавшим плоскостям α 1, α 2, α 3).
Рассмотрим отдельно случай, когда совпадают плоскости α 2 и α 3, т.е. 3-е уравнение можно считать следствием 2-го и отбросить его. Оставшиеся уравнения запишем в виде:
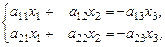 (36)
(36)
причем в этой записи считаем, что не равен нулю определитель:
 , (37)
, (37)
Далее, используя формулы Крамера (9) для случая  , присваивая произвольные значения переменной x 3, будем вычислять соответствующие значения x 1, x 2:
, присваивая произвольные значения переменной x 3, будем вычислять соответствующие значения x 1, x 2:
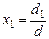 ,
,  , (38)
, (38)
или:
 ,
, 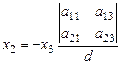 , (39)
, (39)
Учитывая, что неизвестные x 1, x 2, x 3 участвуют в уравнениях равноправно, получим для их вычисления симметричные выражения. Для этого рассмотрим вспомагательный определитель:
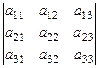 ,
,
и его алгебраические дополнения:
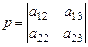 ,
,  ,
,  . (40)
. (40)
Используя (40), получим симметричные выражения для неизвестные x 1, x 2, x 3:
 ,
,  ,
, 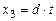 , (41)
, (41)
где t может принимать произвольные значения. Если параметр t определить как время, и принять, что при значении t = 0 некоторая точка находилась в начале координат O (0, 0, 0), то, двигаясь со скоростью v =(p, q, d), в момент времени t движущаяся точка будет находиться в точке X(x 1, x 2, x 3 ).
☺ Пример 21. Вычислим определитель: 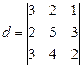 .
.
Решение: Используя определение определителя 3-го порядка и учитывая его свойства, вычислим определитель несколькими способами:
Способ 1. В соответствии с определением определителя 3-го порядка:
 .
.
Способ 2. Воспользуемся Свойством 9, и вычислим данный определитель 3-го порядка разложением по 1-й строке:
 .
.
Способ 3. Воспользуемся Св. 9, и вычислим данный определитель разложением по 2-й строке, но предварительно (см. Св.8) упростим его:
 .
.
Действия: 1) из 2-го столбца вычли 3-й; 2) из 2-й строки вычли 3-ю; 3) к 1-му столбцу прибавили 3-й: в результате во второй строке все нули, кроме одной 1; 4) по Св.9 записали разложение по 2-й строке; 5) вычислили один определитель 2-го порядка.
Вывод: вычисление определителя 3-го порядка Способом 3 значительно упрощает вычислительные трудности при счете вручную.
Ответ: 1.
Пример 22. Заданы три плоскости: 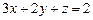 ;
;  ,
,  . Опреде-лим, имеют ли они одну общую точку или несколько.
. Опреде-лим, имеют ли они одну общую точку или несколько.
Решение: Для решения задачи:
1) составим определитель: 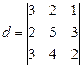 из коэффициентов при неизвестных x, y, z;
из коэффициентов при неизвестных x, y, z;
2) вычислим определитель одним из способов, приведенных в примере 22: результат вычислений определителя  .
.
Вывод: заданные плоскости имеют только одну общую точку.
Ответ: Плоскости пересекаются в одной точке.
☻ Решите примеры:
Пример 23. Вычислите определитель:  .
.
Пример 24. Вычислите определитель:  .
.
Пример 25. Вычислите определитель: 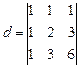 .
.
Пример 26. Вычислите определитель:  , где ω =
, где ω = 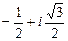 .
.
Вопросы для самопроверки:
1. Может ли определитель 3-го порядка не быть числом?
2. Изменится ли определитель 3-го порядка, если в нем строки заменить столб-цами и наоборот (проверьте!)?
3. Изменится ли определитель 3-го порядка, если в нем строки (или столбцы) поменять местами (проверьте!)?
4. Изменится ли определитель 3-го порядка, если в нем из одной строки вычесть другую строку (проверьте!)?
5. Изменится ли определитель 3-го порядка, если в нем из одного столбца вычесть другой столбец (проверьте!)?
6. Изменится ли определитель 3-го порядка, если в нем строку умножить на число 2 (проверьте!)?
7. Существует ли определитель для матрицы: 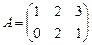 ?
?






