Теорема 1: Определитель произведения нескольких матриц n-го порядка равен произведению определителей этих матриц.
Замечание: теорема остается верной для любого из возможных правил умножения матрицы на матрицу: 1) «строка х строка», 2) «строка х столбец», 3) «столбец х строка», 4) «столбец х столбец».
Говорят, что квадратная матрица невырожденная, если ее определитель не равен нулю.
Следствие: Произведение нескольких невырожденных квадратных матриц - невырожденная матрица.
☺ Пример 27. Имеются матрицы 
и 
. Составлено произведение этих матриц А ∙ В = С. по каждому из возможных правил (см. замечание к теореме). Покажем выполнение теоремы умножения определителей при любом принимаемом правиле умножения матриц (без изменения их порядка!).
Решение: Вычисления проведем по следующей схеме:
1) Вычислим определитель матрицы А: 1-й шаг: 2С-1С; 3С-1С; 2-й шаг: 1R-2Rx2; 3-й шаг: разложение определителя по 3-му столбцу; 4-й шаг: вычисление определителя 2-го порядка:
| 1 | 2 | 3 | 1 шаг | 1 | 1 | 2 | 2 шаг | 7 | 3 | 0 | 3 шаг | 7 | 3 | 4 шаг |
| 3 | 4 | 2 | = | 3 | 1 | 1 | = | 3 | 1 | -1 | =(-1)∙(-1)2+3 | 4 | 1 | = -5 |
| 4 | 5 | 4 | 4 | 1 | 0 | 4 | 1 | 0 |
2) Вычислим определитель матрицы В: 1-й шаг: 3R-2R; 2-й шаг: 3С-2С; 3-й шаг: разложение определителя по 3-й строке; 4-й шаг: вычисление определителя 2-го порядка:
| 2 | -3 | 1 | 1 шаг | 2 | -3 | 1 | 2 шаг | 2 | -3 | 4 | 3 шаг | 2 | 4 | 4 шаг |
| 1 | -4 | 3 | = | 1 | -4 | 3 | = | 1 | -4 | 7 | =(-1)∙(-1)3+2 | 1 | 7 | = 10 |
| 1 | -5 | 2 | 0 | -1 | -1 | 0 | -1 | 0 |
3) Используя результаты п.1,2), можем записать произведение определителей:
4) Используя правило произведения матриц «строка х строка», запишем матрицу:
.
5) Вычислим определитель матрицы С1: 1-й шаг: 3R-2R; 2R-1Rx4; 2-й шаг: 1R+3R; 3-й шаг: разложение определителя по 1-му столбцу; 4-й шаг: вычисление определителя 2-го порядка:
| -1 | 2 | -3 | 1 шаг | -1 | 2 | -3 | 2 шаг | 0 | 5 | -3 | 3 шаг | 5 | -3 | 4 шаг |
| -4 | -7 | -13 | = | 0 | -15 | -1 | = | 0 | -15 | -1 | =(1)∙(-1)3+1 | -15 | -1 | = -50 |
| -3 | 5 | -13 | 1 | 3 | 0 | 3 | 0 |
6) Используя правило произведения матриц «строка х столбец», запишем матрицу:
.
7) Вычислим определитель матрицы С2: 1-й шаг: 2С+3Сх2; 3С-1Сх2; 2-й шаг: 2R-3R; 3R-1Rх2; 3-й шаг: 3R-2Rх2; 3R-1Rх2; 4-й шаг: разложение определителя по 2-му столбцу; 5-й шаг: вычисление определителя 2-го порядка:
| 7 | -26 | 13 | 1 шаг | 7 | 0 | -1 | 2 шаг | 7 | 0 | -1 | 3 шаг | 7 | 0 | -1 | 4 шаг | -1 | 5 шаг | |
| 12 | -35 | 19 | = | 12 | 3 | -5 | = | -5 | 1 | 2 | = | -5 | 2 | =(1)∙(-1)3+1 | -9 | = -50 | ||
| 17 | -52 | 27 | 17 | 2 | -7 | 3 | 2 | -5 | -9 |
8) Используя правило произведения матриц «столбец х строка», запишем матрицу:
.
9) Вычислим определитель матрицы С3: 1-й шаг: 1R-2R; 2R-1Rx4; 2-й шаг: разложение определителя по 1-й строке; 3-й шаг: вычисление определителя 2-го порядка:
| -3 | 1 | -6 | 1 шаг | 0 | 0 | 2 шаг | -3 | 1 | 3 шаг | |
| -3 | 1 | -8 | = | -3 | 1 | -8 | =(2)∙(-1)1+3 | 4 | 7 | = -50 |
| 4 | 7 | 1 | 4 | 7 | 1 |
10) Используя правило произведения матриц «столбец х столбец», запишем матрицу:
.
11) Вычислим определитель матрицы С4: 1-й шаг: 2С+3Сх2; 2-й шаг: 3С-1Сх2; 3-й шаг: 1С-2Сх9; 4-й шаг: разложение определителя по 2-му столбцу; 5-й шаг: вычисление определителя 2-го порядка:
| 9 | -35 | 18 | 1 шаг | 9 | 1 | 18 | 2 шаг | 9 | 1 | 0 | 3 шаг | 0 | 0 | 4 шаг | -2 | 5 шаг | ||
| 13 | -47 | 24 | = | 13 | 1 | 24 | = | 13 | 1 | -2 | = | 4 | 1 | -2 | =(1)∙(-1)1+2 | -7 | = -50 | |
| 12 | -37 | 17 | 12 | -3 | 17 | 12 | -3 | -7 | -3 | -7 |
12) Доказано для любого из правил умножения матриц верно:
▬► 
Ответ: Теорема умножения определителей выполняется при любом принимаемом правиле умножения матриц (без изменения их порядка!).
Пример 28. Имеются матрицы и . Составлены произведения этих матриц А ∙ В = С и В ∙ А = D. Сравним определители матриц С и D.
Решение: Вычисления проведем по следующей схеме:
1) Используя правило произведения матриц «строка х столбец», запишем:
,
где d11 = 2∙1 +(-3)∙3 +1∙4 = -3, d12 = 2∙2 +(-3)∙4 +1∙5 = -3,
d13 = 2∙3 +(-3)∙2 +1∙4 = 4,
d21 = 1∙1 +(-4)∙3 +3∙4 = 1, d22 = 1∙2 +(-4)∙4 +3∙5 = 1,
d23 = 1∙3 +(-4)∙2 +3∙4 = 7,
d31 = 1∙1 +(-5)∙3 +2∙4 = -6, d32 = 1∙2 +(-5)∙4 +2∙5 = -8,
d33 = 1∙3 +(-5)∙2 +2∙4 = 1,
2) Вычислим определитель матрицы D: 1-й шаг: 1R+2Rх3; 2-й шаг: 2 -й шаг: разложение определителя по 1-й строке; 3-й шаг: вычисление определителя 2-го порядка:
| -3 | -3 | 4 | 1 шаг | 0 | 0 | 2 шаг | 1 | 1 | 3 шаг | |
| 1 | 1 | 7 | = | 1 | 1 | 7 | =(25)∙(-1)1+3 | -6 | -8 | = -50 |
| -6 | -8 | 1 | -6 | -8 | 1 |
Ответ: Теорема умножения определителей выполняется при любом принимаемом правиле умножения матриц и при любом их порядке!.
☻ Решите примеры:
Пример 29. Имеются матрицы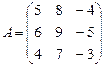 
и 
. Составьте произведение этих матриц А ∙ В = С. по каждому из возможных правил (см. замечание к теореме). Покажите выполнение теоремы умножения определителей при любом принимаемом правиле умножения матриц (без изменения их порядка!).
Пример 30. Имеются матрицы 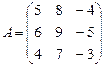и . Составьте произведения этих матриц А ∙ В = С и В ∙ А = D. Сравните определители матриц С и D.
Вопросы для самопроверки:
1. При каких условиях квадратная матрица С =А ∙ В имеет определитель, равный нулю?
2. Для матриц А и В составлены произведения А ∙ В = С и В ∙ А = D. При каких условиях возможно равенство: 
?
3. Для матриц А и В составлены произведения А ∙ В = С и В ∙ А = D. Может ли матрица С быть невырожденной, а матрица D вырожденной?
