Вычисление определителей 4-го и более высоких порядков не может быть представлено достаточно простой «геометрической схемой», как это сделано для определителей 2-го и 3-го порядков.
Для определения и изучения определителей n -го порядка используются понятия, относящиеся к конечным множествам некоторых элементов.
4.1. Перестановки.
Рассмотрим множество М целых чисел: 1, 2, …, n. Элементы множества М можно расположить разными способами.
Определение: всякое расположение чисел 1, 2, …, n в некотором порядке называется пе-рестановкой из n чисел. Общий вид записи перестановки из n элементов:
i 1, i 2, …, in, (42)
где каждое is есть одно из чисел 1, 2, …, n, причем ни одно из этих чисел не встречается дважды и не пропущено.
В качестве i 1 можно выбрать любое из чисел 1, 2, …, n. Это дает n различных возможностей. Если i 1 уже выбрано, то в качестве i 2 можно выбрать лишь одно из оставшихся (n -1) чисел, т.е. различных способов выбрать числа (символы) i 1 и i 2 равно произведению n∙ (n -1) и т.д. Число перестановок из n символов равно произведению:
Если в некоторой перестановке поменяем местами какие-либо два символа (не обязательно стоящие рядом), а все остальные оставим на месте, то получим новую перестановку. Такое преобразование перестановки называется транспозицией.
Теорема 1. Все перестановки из n символов можно расположить в таком порядке, что каждая следующая перестановка получается из предыдущей одной транспозицией, причем начинать можно с любой перестановки.
► При n =2 утверждение справедливо: 1, 2 → 2, 1;
2, 1 → 1, 2.
Рассмотрим все перестановки из n элементов, у которых на первом месте стоит символ i 1. Таких перестановок 
и их можно упорядочить в соответствии с требованиями теоремы для (n -1) символов. Пусть последняя из таких перестановок (с учетом того, что символ i 1 был все время неперемещаем) имеет вид:
i 1, i 2, …, in (43)
В перестановке (43), содержащей n символов, совершим транспозицию символа i 1 с любым другим (например, с символом i 2) и вновь упорядочим все перестановки из (n -1) символов при фиксированном на первом месте i 2 и т.д. Так можно перебрать все перестановки из n символов. ◄
Следствие: от любой перестановки из n символов можно перейти к любой другой перестановке из тех же символов при помощи нескольких транспозицией.
Если в перестановке символ i 1 стоит раньше, чем символ i 2, но 
, то говорят, символы i 1 и i 2 составляют инверсию (нарушение порядка), иначе указанные символы составляют порядок. Перестановка называется четной, если ее символы составляют четное число инверсий, и нечетной – в противном случае.
Замечание: 1) всякая транспозиция меняет четность перестановки.
2) сумма порядков и инверсий постоянна и равна 
☺ Пример 31. Определим четность перестановки 1, 2, …, n.
Решение: Заданная перестановка четная, т.к. в ней нет инверсий (нарушений порядка).
Ответ: Четная.
Пример 32. Определите четность перестановки 4 5 1 3 6 2.
Решение: Для подсчета числа инверсий воспользуемся таблицей 1, в которой указаны инверсии выделяемых элементов со всеми последующими (учет нарушений порядка).
| ╙ | ☼ | ☼ | ☼ | =3 | ||||
| ╙ | ☼ | ☼ | ☼ | =3 | ||||
| ╙ | =0 | |||||||
| ╙ | ☼ | =1 | ||||||
| ╙ | ☼ | =1 | ||||||
| —————————————————— | ||||||||
| Число инверсий: | =8 |
Ответ: Четная.
☻ Решите примеры:
Пример 33. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.
Пример 34. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?
Пример 35. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.
Вопросы для самопроверки:
1. Перестановка – это матрица?
2. Что такое «транспозиция» двух элементов перестановки?
3. Что такое «инверсия» для двух выделенных элементов перестановки?
4. Что такое «порядок» для двух выделенных элементов перестановки?
5. Чему равна сумма числа инверсий и числа порядков в любой перестановке чисел 1, 2, …, 99.
4.2. Подстановки.
Определение: Запишем одну перестановку под другой: 
. Эту запись
называют подстановкой, понимая под этим отображение (соответствие) множества символов, состоящего из первых n чисел: 1, 2, …, n, на себя: 
; 
, 
, …, 
Если учесть, что подстановка как отображение множества чисел 1, 2, …, n не меняется при транспозиции столбцов, выберем для нее простейшее выражение:
, (44)
где α i – число, в которое переходит число i.
В выражении (44) подстановки порядка n различаются только перестановками в нижней строке записи, т.е. подстановку однозначно определяет перестановка, записан-ная в ее нижней строке. Это значит, что всего подстановок порядка n столько же, сколь-ко и перестановок, т.е. 
.
Определим понятие четности для подстановок:
А. Исходя из общего определения подстановки:
- подстановка четная, если четности верхней и нижней перестановок совпадают;
- подстановка нечетная, если четности верхней и нижней перестановок противоположны.
Б. Учитывая частную запись подстановки (44):
- подстановка четная, если ее определяет четная перестановок;
- подстановка нечетная, если ее определяет нечетная перестановка.
Кроме подсчета числа инверсий в перестановках для определения четности подстановок применяют также разложение их в циклы. Воспользуемся этим приемом (не обосновывая его, примем на веру), рассмотрев конкретный пример.
☺ Пример 36. Определим четность подстановки 
.
Решение: Для определения четности подстановки разложим ее в произведение циклов:
,
где скобки после знака “=” отражают циклы: (1→6→3→1), (2→5→2), (4→4), (7→7), (8→8), (9→9) отображения символов 1,2,…,9 по определению подстановки (в циклах учтены также символы «остающиеся на месте»). Имея разложение подстановки в циклы, определим число декремент: d = n – s, где n – порядок подстановки, s – число циклов в разложении подстановки. В рассматриваемом примере: d = 9 – 6 = 3 – нечетное число → подстановка нечетная.
Ответ: Четная.
Пример 37. Для определения четности подстановки разложим ее в произведение циклов:
,
где скобки после знака “=” отражают циклы: (1→5→1), (2→8→6→4→2),(3→9→7→3) отображения символов 1,2,…,9 по определению подстановки. Вычислим декремент для рассматриваемой подстановки: d = 9 – 3 = 6 – четное число → подстановка четная.
☻ Решите примеры:
Пример 38. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.
Пример 39. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?
Пример 40. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.
Вопросы для самопроверки:
6. Подстановка – это матрица?
7. Что такое «транспозиция» столбцов подстановки?
8. Что такое «инверсия» в подстановке?
9. Что такое «порядок» в подстановке?
10. Чему равна сумма числа инверсий и числа порядков в любой подстановке чисел 1, 2, …, 99.
Определители n-го порядка
Пусть имеем квадратную матрицу n -го порядка:
, (45)
элементами aij, которой могут быть элементы любого числового поля. Рассмотрим всевозможные произведения по n элементов, расположенных в разных строках и разных столбцах:
, (46)
где 
- составляют некоторую перестановку из чисел 1, 2, …, n. Число таких произведений равно числу перестановок, т.е. .
Составим подстановку из n символов: . (47)
Можно заметить, что в определителях 2-го и 3-го порядков со знаком “плюс” входят те члены определителей, индексы которых составляют четную подстановку, а со знаком “минус” – члены с нечетной подстановкой индексов. Это свойство сохраняют в определении определителей n-го порядка.
Определение: определителем n -го порядка, соответствующим матрице (45), называется алгебраическая сумма членов, составленная следующим образом:
- каждый член определителя (отдельное слагаемое в указанной сумме) есть произведение n элементов определителя, взятых по одному из каждого столбца и каждой строки матрицы;
- член определителя берется со знаком “плюс”, если индексы составляют четную подстановку, и со знаком “минус”, если нечетную:
Обозначение определителя: 
(48)
Применение определения определителя n -го порядка для практических вычислений было бы затруднительно. Исследуем его свойства, непосредственно вытекающие из определения.
Учитывая свойство1 определителей 3-го порядка, устанавливающее равноправие строк и столбцов определителя, транспонируем матрицу А и запишем:
, 
(49)
Пусть в определителе 
выделен некоторый член:
, (50)
для определения знака которого используется подстановка n -го порядка:
, (51)
в ней верхняя перестановка отражает номера строк определителя, в которых размещены элементы матрицы, входящие в выражение (50); а нижняя – номера столбцов.
После транспонирования матрицы А те же элементы будут участвовать в выражении члена определителя матрицы 
:
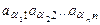, (52)
причем для определения знака, который будет иметь этот член в определителе должна использоваться подстановка:
, (53)
Очевидно, четности подстановок (51) и (53) совпадают (см. определение четности подстановки).
Нами доказано одно из важнейших свойств определителя n -го порядка (теперь уже для всех n = 2, 3, …):
Свойство 1. Определитель не меняется при транспонировании матрицы: 
.
Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю (следует из того, что какой-то из нулей этой строки обязательно войдет в выражение каждого из членов определителя).
Свойство 3. Если в определителе переставлены две строки (столбца), то все члены полученного определителя те же, что и в исходном, но с обратным знаком, т.е. перестановка двух строк определителя меняет его знак (следует из представленной ниже схемы преобразования определителя и соответствующих подстановок: их четности поменялись!):
| 
|
|
| ||||||||||||
| | | | | | | | | ||||||||||||
| | | | | | | | | ||||||||||||
| i | ─ | ─ | ☼ | ─ | ┼ | ─ | ─ | i | ─ | ─ | ┼ | ─ | ☼ | ─ | ─ |
| | | | | | | | | ||||||||||||
| j | ─ | ─ | ┼ | ─ | ☼ | ─ | ─ | j | ─ | ─ | ☼ | ─ | ┼ | ─ | ─ |
| | | | | | | | | ||||||||||||
| | | | | | | | |
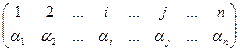
Свойство 4 Определитель, имеющий две одинаковые строки, равен нулю (при перестановке этих строк из свойства 3 следует, что d = -d, т.е. d = 0).
Свойство 5 Если все элементы i -й строки определителя умножить на произвольное число k, то определитель умножается на число k (следует из выражения (48) записи общего члена определителя: каждый член определителя содержит ровно один элемент из i -й строки, поэтому всякий из них приобретает множитель k, т.е. сам определитель умножается на k.
Свойство 6 Определитель, содержащий две пропорциональные строки, равен нулю (следует из свойств 5 и 4).
Свойство 7 Если все элементы i -й строки определителя имеют вид: 
, где j = 1, 2, …, n, то определитель равен сумме двух определителей, у которых все строки, кроме i -й, такие же, как в заданном определителе, а i -я строка в одном из определителей состоит из элементов bij, а в другом – из элементов cij.
Свойство 8 Если одна из строк определителя есть линейная комбинация других его строк, то определитель равен нулю (следует из последовательного применения свойств 7, 6, 5, 4).
Свойство 9 Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой, умноженной на одно и то же число (следует из свойств 7 и 6). Обобщение: определитель не меняется, если к одной из его строк прибавляется линейная комбинация других его строк.
Вычислять определитель, исходя из его определения, т.е. выписывая n! его членов и определяя их знаки, было бы затруднительно. Разработаны способы, позволяющие вычислять определитель n -го порядка через определители более низкого порядка.
Минор k-го порядка М.
Пусть имеем определитель n -го порядка. Для целого числа k: 
выбираем в определителе k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу порядка k. Определитель этой матрицы называется минором k -го порядка определителя d. Наоборот, можно С и (n-k) столбцов – останется минор k -го порядка. Ниже приведена схема выделения минора k -го порядка вычеркиванием k строк и k столбцов:
| | | | | | | ☼ | ☼ | ☼ | ─ | ─ | ─ | ─ | ||||||
| ─ | ☼ | ─ | ☼ | ☼ | ─ | ─ | ☼ | ☼ | ☼ | ─ | ─ | ─ | ─ | ||
| | | | | | | ☼ | ☼ | ☼ | ─ | ─ | ─ | ─ | ||||||
| ─ | ☼ | ─ | ☼ | ☼ | ─ | ─ | ▬► | | | | | | | |||||
| | | | | | | | | | | | | ||||||||||
| ─ | ☼ | ─ | ☼ | ☼ | ─ | ─ | | | | | | | ||||||
| | | | | | | | | | | | |
Определитель (минор), получаемый вычеркиванием k строк и k столбцов, обозначим М, а одновременно с ним выделяемый минор (n-k) порядка обозначим –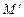 
, его называют “ дополнительный минор для минора М порядка k. В частном случае можно вычеркнуть минор 1-го порядка: элемент 
, тогда минор 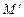будет иметь (n-k) порядок.
